17. Диффузия носителей заряда. Диффузионная длина

Если в полупроводнике носители заряда распределены неравномерно, возникает диффузия носителей заряда. Она может быть описана известным законом Фика:

J_p = - D_p grad p (1)

или

J_n = - D_n grad n (2)

Здесь J_p, J_n - плотности потоков дырок, электронов, равные числу частиц, пересекающих в единицу времени единичную площадку, перпендикулярную направлению градиента концентрации;

D_p, D_n – коэффициенты диффузии.

Подвижные носители заряда являются заряженными частицами, поэтому их направленное движение является электрическим током. Плотность тока может быть найдена путем умножения плотности потока частиц (1) на элементарный заряд q для дырок или – на (-q) для электронов.

j_p = - q D_p grad p (3)

или

j_n = q D_n grad n. (4)

Если в какой-либо части полупроводника создана избыточная концентрация неравновесных носителей заряда, то одновременно с процессом диффузии происходит их рекомбинация. Поэтому избыточная концентрация уменьшается в направлении от места источника этой избыточной концентрации. Найдем закон изменения избыточной концентрации носителей, например дырок, от расстояния.

В уравнение (1) – уравнение непрерывности – добавим еще одно слагаемое:

. (5)

В стационарном случае

, (6)

тогда подставим (3) в(5) и приравняем к нулю

; (7)

после преобразований получим

(8)

Здесь - оператор Лапласа.

В одномерном случае оператор Лапласа равен

d²p/dx².

. (9)

Решение этого уравнения имеет вид:

. (10)

Коэффициенты А₁ и А₂ найдем из граничных условий.

При , откуда А₁=0;

при , откуда А₂= p₀.

Окончательно получим

(11)

или

. (12)

Здесь - диффузионная длина.

(Аналогично для электронов .)

Расстояние, на котором пpи одномерной диффузии в полупpоводнике без электрического поля в нем избыточная концентpация носителей заряда уменьшается вследствие рекомбинации в е раз, называют диффузионной длиной.

Можно показать, что диффузионная длина pавна среднему расстоянию, на которое диффундируют носители за вpемя жизни.

Замечание: не следует путать диффузионную длину ни со средней длиной свободного пробега носителей, которая определяется как среднее расстояние, проходимое носителем между двумя последовательными актами рассеяния, ни с длиной волны де Бройля, равной h/mv.

Диффузионная длина очень важная характеристика, её вносят в марку материала.

Пример: ГЭС 1,0/0,5 - германий электронный, легированный сурьмой, с удельным сопротивлением 1,0 Ом^.см и диффузионной длиной 0,5 мм; или ЭКДБ 10/1,0 - эпитаксиальный кремний, легированный бором с удельным сопротивлением 10 Ом^.см и диффузионной длиной 1 мм.

Связь между диффузионой длиной, коэффициентом диффузии и временем жизни нервновесных носителей:

;

18. СООТНОШЕНИЕ ЭЙНШТЕЙНА МЕЖДУ ПОДВИЖНОСТЬЮ И КОЭФФИЦИЕНТОМ ДИФФУЗИИ НОСИТЕЛЕЙ ЗАРЯДА

; (1)

(2)

Напряженность электрического поля

; (3)

где  -потенциал.

Потенциальная энергия дырки равна q. При отсутствии вырождения распределение дырок в потенциальном поле подчиняется закону Больцмана:

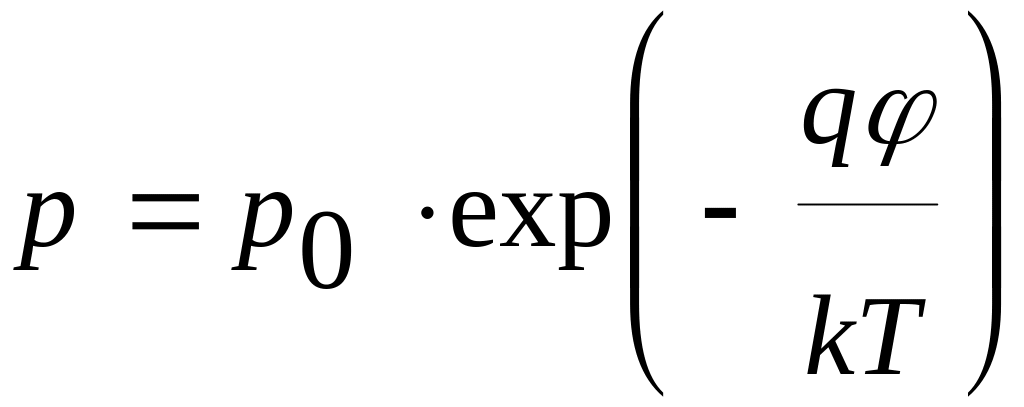, (4)

. (5)

. (6)

. (7)

Уравнения, связывающие коэффициент диффузии носителей заpяда, подчиняющихся статистике Максвелла-Больцмана, с их подвижностью в условиях термодинамического равновесия носят название соотношений Эйнштейна.

Замечание: Соотношение Эйнштейна применимо и к неравновесным носителям, что подтверждено экспериментально.

31