3. Линейное, угловое, продольное увеличения идеальной системы. Связь между ними. Расчет линейного увеличения различными способами (инвариант Аббе, формулы Ньютона и Гаусса, уравнение нулевых лучей).

Идеальной ОС наз-ют ОС, отображающую каждую точку предмета точкой и сохраняющую заданный масштаб изображения.

Линейным увеличением β ОС наз-ют отношение линейного размера изобр-я в направлении, перпендикулярном опт оси, к соответствующему р-ру предмета также в направлении, перпендикулярном опт оси: β=у’/у.

Угловым увеличением γ ОС наз-ют отношение tg угла м/у лучом и опт осью в пространстве изобр-й к tg угла м/у лучом и опт осью в пространстве предметов:

(из рис.) (*)

Продольным увеличением α ОС наз-ют отношение ∞-но малого отрезка, взятого вдоль опт оси в пространстве изображений, к сопряженному с ним отрезку в пространстве предметов:

Связь между увеличениями:

Для ОС в однородной среде:

Расчет линейного увеличения различными способами (инвариант Аббе, формулы Ньютона и Гаусса, уравнение нулевых лучей).

Инвариант Аббе, практическое применение.

Приближении лучей, распространяющихся близко к оптической оси, т.е. почти с нулевой апертурой, в параксиальном приближении, оптическая система, чтобы быть абсолютной, то есть давать стигматическое и подобное изображение предметной плоскости, должна удовлетворять инварианту Аббе:

,

где n₀ и n₁ – показатели преломления в пространствах предмета и изображения r – радиус кривизны поверхности, z₀ - Z-координата осевой точки предмета, а z₁ – изображения.

Инвариант Аббе может быть преобразован к виду: здесь Φ – называется оптической силой поверхности.

Кроме того, главные плоскости проективного преобразования совпадают и проходят через вершину сферической поверхности. То есть, главные точки совпадают с полюсом сферической поверхности.

Устремляя в инварианте Аббе поочерёдно z₀ и z₁ к минус и плюс бесконечности, находим аппликаты фокусов:

.

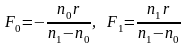В отличие от коллинеарной оптики, где начало координат помещают в точки фокусов, в параксиальной оптике, поддерживаемой ГОСТ 7427-76, фокусные расстояния отсчитывают от главных плоскостей, поэтому фокусные расстояния определяются соотношениями:

.

Используя, соотношение для оптической силы поверхности, получаем соотношение: .

То есть оптическая сила может вычисляться по параметрам как среды в пространстве предметов (со знаком минус), так и в среде пространства изображения (со знаком плюс).

Формулы Ньютона, Гаусса.

П усть система задана положением кардинальных элементов; определим зависимость между расстояниями сопряженных точек А и А’ до точек фокусов и фокусными расстояниями системы. Положение предмета АВ = у (рис.1) относительно переднего фокуса определяется отрезком z, отсчитываемым от точки F. Изображение крайней внеосевой точки В построено с помощью двух лучей, идущих из точки В: один – параллельно оптической оси, другой – через передний фокус. Точка пересечения сопряженных с ними лучей в пространстве изображений является крайней внеосевой точкой В’ изображения –y’. Положение изображения A’B’ = y’ относительно заднего фокуса определяется отрезком z’. Пользуясь подобием одинаково заштрихованных треугольников на рис.1, имеем соотношения (при h = h’ = y; h1 = h1’ = y’):

в пространстве предметов ;

в пространстве изображений .

Приравняв их друг другу, получим формулу Ньютона

(1)

и расчетную формулу для линейного увеличения

(2)

Используя соотношение между передним и задним фокусами оптической системы , выражение (1) преобразуем к виду

.

Для системы, расположенной в однородной среде, формула Ньютона принимает вид .

Обозначим на рис.1: НА = -а = -z-f; H’A’ = a’ = z’+f’, и преобразуем выражение (1) с учетом этих соотношений. Имеем .

Разделив почленно на аа’, получим формулу Гаусса или формулу отрезков.

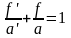или ,

где называют оптической силой системы.

Заменим в формуле (2) z и z’ на a-f и a’-f’ соответственно. Тогда

, ,откуда имеем 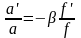. Зная отрезки а и а’, можно определить линейное увеличение ОС.

.

Нулевые лучи. Уравнения углов и высот.

Нулевой луч – фиктивный луч, преломляющийся на главных плоскостях поверхностей, но встречающиеся с ними на конечных расстояниях от оптической оси и отсекает те же отрезки на оси, что и параксиальный луч.

Углы для нулевого луча незначительно отличаются от и для реальных лучей, то формулы легче

После преобразования получим формулу для луча выходящего

Используя это мы можем просчитывать нулевой луч через любое количество поверхностей.

Пусть система состоит из P поверхностей

Формулы расчетов углов через поверхности называют уравнением углов нулевого луча. Применим (1) для каждой поверхности получим уравнение в общем виде:

(2)- уравнение углов

(3)- уравнение высот

Иногда известен ход нулевого луча, т.е. известны углы и , можно определить необходимые радиусы кривизны.

Последовательность использования углов нулевого луча (2) с учетом (3) позволяет рассчитывать ход луча через серию преломляющих и отражающих поверхностей.