2. Статистическая оценка интенсивности восстановлений систем железнодорожной автоматики и телемеханики

ТУ и ТЗ устанавливают требования к минимальному уровню надежности технических средств (значения показателей надежности ограничиваются словами «не менее» - для значений наработки на отказ, «не более» - для значений интенсивности отказов). Технические средства ЖАТ разрабатываются с учетом запаса надежности. На практике в большинстве случаев реальный уровень надежности технических средств значительно выше, чем установленный ТЗ или ТУ. Это подтверждают полученные значения А_э (табл. 4).

Следует отметить, что при определении показателей А_э и А_н для некоторых систем и устройств условные измерители могут различаться (табл. 4). Так, например, среднесетевое эксплуатационное значение интенсивности отказов А_э для систем АБ составляет 7,85-10^-06 1/ч на километр, а для конкретной системы, например АБ-ЧКЕ, А_н = 1,85-10^-05 1/ч на сигнальную точку.

Этим можно объяснить разницу в значениях показателей надежности для ряда систем и устройств ЖАТ, которая в отдельных случаях может достигать нескольких порядков (табл. 4).

Поэтому для адекватной оценки и сопоставимости реального уровня надежности и требований, установленных в ТУ, целесообразно проводить оценку показателей эксплуатационной надежности, а также устанавливать требования в ТУ, используя одинаковые условные измерители (для каждого из видов технических средств - свои).

Для различных систем и устройств возможно использовать различные условные измерители, по отношению к которым определяются показатели надежности. В таблице 5 приведены предпочтительные условные измерители для систем и устройств ЖАТ.

Таблица 5 – Условные измерители для систем и устройств ЖАТ

Система, устройство	Условный измеритель нормирования
Электрическая и горочная централизации	Централизованная стрелка
Диспетчерская централизация	1 км, оборудованный системой, или управляемый, контролируемый объект
Автоблокировка	1 км, оборудованный системой, или сигнальная точка
Полуавтоматическая блокировка	1 км, оборудованный системой, или перегон
Переездная сигнализация	Переезд
Автоматическая локомотивная сигнализация	1 км, оборудованный системой
Система счета осей	Комплект
УКСПС	Система
САУТ	Точка САУТ
Стрелочные электроприводы	Устройство
Светофоры	Устройство
Релейные шкафы	Устройство
Аккумуляторы	Устройство
Кабели СЦБ	1 км длины

На основе вариационного ряда строится гистограмма распределения случайной величины, представляющая собой эмпирическую функцию плотности распределения вероятности. В ней по горизонтальной оси последовательно, по мере их возрастания, откладываются интервалы изменения экспериментальных значений, на каждом из которых, строится прямоугольник высоты .

Пример эмпирической плотности распределения вероятности для распределения , близкого к нормальному (гауссовскому), представлен на рисунке 6.

Рисунок 6 – Эмпирическая плотность распределения вероятности

На основании визуального анализ гистограммы подбирается теоретическая функция плотности распределения график которой схож с гистограммой. Такая функция будет использована для «сглаживания» гистограммы. Чаще всего в качестве такой функции выбирается один из известных законов: нормальный, экспоненциальный, Вейбулла и т.п.

При использовании вариационного ряда оценка математического ожидания есть выборочная средняя:

,

где – представляет собой значение параметра, соответствующее середине q-го интервала:

,

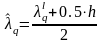где 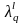– значение, соответствующее левой границе подынтервала.

В качестве оценки второго момента используется выборочная дисперсия, вычисляемая по формуле:

.

Вместе с тем выборочная дисперсия, в отличие от выборочной средней является смещенной оценкой, поэтому используется поправка:

.

Помимо дисперсии часто используют связанную с ней величину, называемую «исправленным» средним квадратическим отклонением:

.

Подстановкой вычисленных параметров в формулу «сглаживающей» вероятностной функции можно конкретизировать распределение. Пример, для случая использования в качестве сглаживающего нормального (гауссовского) распределения представлен на рисунке 7.

Рисунок 7 – Эмпирическая и теоретическая плотность распределения вероятности

В случае, если параметры не есть непосредственно моменты случайной величины, то они определяются через и .

Примеры наиболее распространенных теоретических распределений, с основными характеристиками, а также их графические изображения представлены в таблице 6.

Таблица 6 – Типовые вероятностные распределения

Формула плотности вероятности	График плотности вероятности	Числовые параметры распределения
Нормальный закон распределения
		Математическое ожидание: Дисперсия: Определяются непосредственно
Закон равномерной плотности
		Математическое ожидание и дисперсия определяются через значения левой границы интервала а и правой – b:
Экспоненциальный закон распределения
		Математическое ожидание и дисперсия выражаются через интенсивность :
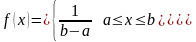