5. Определение зависимости шероховатости выпиливаемых досок от времени работы рамных пил после заточки
Исходные данные:
x — время работы рамных пил после заточки, ч
y — шероховатость поверхности досок, мм
Таблица 5.1
№ |
|
|
|
|
|
1 |
0,5 |
0,25 |
0,2 |
0,40 |
0,16 |
2 |
1,0 |
1,0 |
0,5 |
0,50 |
0,25 |
3 |
1,5 |
2,25 |
0,87 |
0,58 |
0,336 |
4 |
2,0 |
4 |
1,38 |
0,69 |
0,476 |
5 |
2,5 |
6,25 |
1,775 |
0,71 |
0,504 |
∑ |
7,5 |
13,75 |
4,725 |
2,88 |
1,726 |
Определяем коэффициент корреляции r между временем работы пил после заточки и шерохроватости поверхности выпиливаемых досок h.
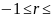
Коэффициент корреляции r вычисляем по формуле:
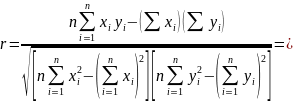
Оценка значимости коэффициента корреляции производится с помощью t-критерия. Для этого определяется:
,
,
следовательно,
, значит принимает гипотезу о некоррелированности величин x и y. В противном случае r значимо отличается от 0, т.е. между величинами x и y существует линейная статическая связь.
Оцениваем коэффициенты регрессии линейной и квадратичной моделей. Регрессионная модель в виде линейного уравнения имеет вид:
Коэффициенты регрессии определяем, решив систему уравнений:
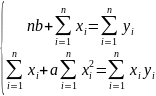
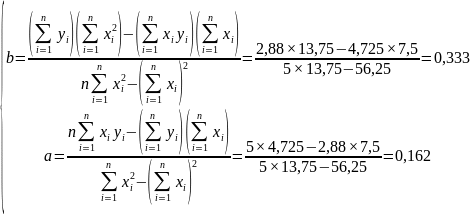
Строим график:
Рис. 5.1
Регрессионная
модель в виде квадратичного уравнения
имеет вид:
Для нахождения трех неизвестных коэффициентов регрессии, решим систему из трех линейных уравнений с тремя неизвестными:
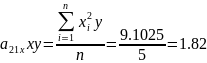
Подставляем все значения в последнее уравнение:
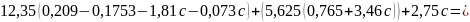
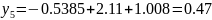
Строим график зависимости:
Рис. 5.2 График зависимости шероховатости досок от времени работы рамных пил
Вывод: в соответствии с проведенным анализом, мы выяснили, что зависимость шероховатости выпиливаемых досок от времени работы рамных пил после заточки определяется по линейной зависимости.
6. Обработка результатов полнофакторного плана и построение регрессионной зависимости производительности трелевочных машин
Исходные данные:
Lтр — среднее расстояние трелевки, м;
Vхл — средний объем хлыста, м3;
Пч — часова производительность, м3/ч
Таблица 6.1
Показатель |
Данные |
|||
Управляемые факторы (X1, X2) |
Расстояние трелевки Lтр, (X1) |
X1min, м X1max, м |
150 450 |
|
Объем хлыста Vхл, (X2) |
X2min, м3 X2max, м3 |
0,10 0,60 |
||
Выходная величина (отклик), Y |
Производительность трелевочного трактора, м3/ч |
1 |
11,0 11,2 11,0 10,5 10,8 |
|
2 |
5,8 6,2 6,0 6,1 5,9 |
|||
3 |
16,1 15,9 16,4 16,8 16,7 |
|||
4 |
9,1 9,8 9,2 8,9 8,8 |
|||
Результаты расчета и эксперимента сводим в таблицу.
Таблица 6.2
Факторы |
Результаты эксперимента |
Результаты расчета |
||||||||||||||||||
Натуральные |
Нормализованные |
y1 |
y2 |
y3 |
y4 |
y5 |
|
|
|
|||||||||||
Lтр,м |
Vхл,м3 |
X1 |
X2 |
|||||||||||||||||
150 |
0,1 |
-1 |
-1 |
11.0 |
11.2 |
11.0 |
10.5 |
10.8 |
10.9 |
0.07 |
|
|||||||||
450 |
0,6 |
+1 |
-1 |
5.8 |
6.2 |
6.0 |
6.1 |
5.9 |
6.0 |
0.025 |
|
|||||||||
150 |
0,1 |
-1 |
+1 |
16.1 |
15.9 |
16.4 |
16.4 |
16.7 |
16.38 |
0.147 |
|
|||||||||
450 |
0,6 |
+1 |
+1 |
9.1 |
9.8 |
9.2 |
8.9 |
8.8 |
9.16 |
0.153 |
|
|||||||||
Определим уровни и интервалы варьирования факторов:
— основной
уровень варьирования фактора;
— интервал
варьирования фактора.
Аналогично находим верхний и нижний уровни варьирования среднего объема хлыста.
Рассчитываем средние и дисперсии для каждой серии опытов по формулам:
Отбрасываем аномальные результаты эксперимента и рассчитываем дисперсию воспромизводимости для каждой серии опытов.
Находим интервал мат. ожидания для каждой выборки:
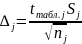
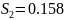
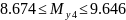
Результаты
эксперимента не входящие в полученные
диапазоны из табл.6.2 удаляем и пересчитываем
значения
и
.
Таблица 6.3
Факторы |
Результаты эксперимента |
Результаты расчета |
|||||||||||||||||
Натуральные |
Нормализованные |
y1 |
y2 |
y3 |
y4 |
y5 |
|
|
|
||||||||||
Lтр,м |
Vхл,м3 |
X1 |
X2 |
||||||||||||||||
150 |
0,1 |
-1 |
-1 |
11.0 |
11.2 |
11.0 |
— |
10.8 |
11,0 |
0.02 |
|
||||||||
450 |
0,6 |
+1 |
-1 |
— |
6.2 |
6.0 |
6.1 |
5.9 |
6.05 |
0.0125 |
|
||||||||
150 |
0,1 |
-1 |
+1 |
16.1 |
— |
16.4 |
16.4 |
16.7 |
16.5 |
0.075 |
|
||||||||
450 |
0,6 |
+1 |
+1 |
9.1 |
— |
9.2 |
8.9 |
8.8 |
9.0 |
0.025 |
|
||||||||
Проверяем нормальность результатов:
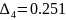
Для
проверки однородности нескольких
дисперсий при равных объемах выборок
может быть использован G-критерий
Кохрена. Пусть
— количество выборочных дисперсий,
однородность которых проверяется.
Обозначим эти дисперсии:
.
Вычислим расчетное G-отношение
по формуле:
По
выбранному уровню значимости q,
числу степеней свободы каждой выборки
и по количеству выборок N
из таблицы распределения Кохрена
выбираем величину
.
,
следовательно гипотеза о однородности
дисперсий неверна.
Вычисляем дисперсию воспроизводимости по формуле:
Число степеней свободы f для данной дисперсии равно:
Рассчитываем
коэффициенты регрессионной модели вида
для нормальных и натуральных факторов.
Находим функции отклика.
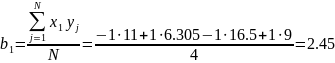
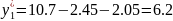
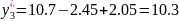
Регрессионная модель в натуральных обозначениях будет иметь вид:
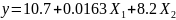
Запишем регрессионную модель в натуральных обозначениях:
Оцениваем степень значимости коэффициентов регрессии:
Вычисленную
величину
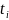сравниваем с табличным значением
критерия Стьюдента для заданного уровня
значимости
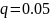и числа степеней свободы
.
Проверка адекватности математической модели даст возможность ответить на вопрос, будет ли построенная модель предсказывать значения выходной величины с той же точностью, что и результаты эксперимента.
Определяем сумму квадратов, характеризующую адекватность модели:
Вычисляем число степеней свободы дисперсии адекватности:
Вычисляем дисперсию адекватности:
C
помощью F-критерия
Фишера проверяем однородность дисперсии
адекватности
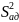и дисперсии воспроизводимости
:
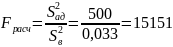
Модель неадекватна.
Строим
графики зависимости
Рис. 6.1 График зависимости в нормальных обозначениях
Рис. 6.2 График зависимости в натуральных обозначениях