- •Содержание. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
- •2. Введение
- •3. Определение процента годной продукции и требуемой точности настройки раскряжевочной установки
- •Исходные данные для определения процента годной продукции и требуемой точности настройки раскряжевочной установки.
- •Данные для построения гистограммы и проверки степени согласования экспериментальных и теоретических законов.
- •5. Определение зависимости шероховатости выпиливаемых досок от времени работы рамных пил после заточки
- •6. Обработка результатов полнофакторного плана и построение регрессионной зависимости производительности трелевочных машин
- •7. Оптимальный раскрой хлыста
- •8. Список использованной литературы
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Санкт-Петербургский государственный лесотехнический университет имени С.М. Кирова
Кафедра технологии лесозаготовительных производств
КУРСОВОЙ ПРОЕКТ
на тему: «Планирование и организация эксперимента».
Выполнил:
Студент ЛИФ IV курс 3 группа
Бачериков И.В
№ зач.кн.: 108033
Проверил:
_________________________
дата _________________________
Санкт-Петербург
2012
1. СОДЕРЖАНИЕ
Содержание. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
ВВЕДЕНИЕ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
ОПРЕДЕЛЕНИЕ ПРОЦЕНТА ГОДНОЙ ПРОДУКЦИИ И ТРЕБУЕМОЙ ТОЧНОСТИ НАСТРОЙКИ РАСКРЯЖЕВОЧНОЙ УСТАНОВКИ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
АНАЛИЗ СТАТИСТИЧЕСКИХ СВОЙСТВ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ ПИЛОМАТЕРИАЛОВ. . . . . . . . . . . . . . . . . . . . 8
ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ ШЕРОХОВАТОСТИ ВЫПИЛИВАЕМЫХ ДОСОК ОТ ВРЕМЕНИ РАБОТЫ РАМНЫХ ПИЛ ПОСЛЕ ЗАТОЧКИ. . . . . . . . . . . . . . . . . . . . 12
ОБРАБОТКА РЕЗУЛЬТАТОВ ПОЛНОФАКТОРНОГО ПЛАНА И ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ ПРОИЗВОДИТЕЛЬНОСТИ ТРЕЛЕВОЧНЫХ МАШИН. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
ОПТИМАЛЬНЫЙ РАСКРОЙ ХЛЫСТА. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2. Введение
Высокие темпы развития теоретических наук на основе проработанного математического аппарата и необходимостью их экспериментального подтверждения требует из-за медленного развития технологий все более дорогостоящих экспериментов. При любом эксперименте невозможно избежать воздействия некоторых неучтенных помех, несмотря на стремление исследователя свести их к минимуму. Большинство из этих воздействий имеет случайную природу. Для возможности их частично компенсировать было разработано целое поднаправление математики — математическая статистика, которая позволяет оценивать параметры с частичным исключением помех.
3. Определение процента годной продукции и требуемой точности настройки раскряжевочной установки
Исходные данные:
n — количество наблюдений;
 — наблюдаемые
длины сортиментов после раскряжевки,
заданные в виде простого статистического
ряда.
— наблюдаемые
длины сортиментов после раскряжевки,
заданные в виде простого статистического
ряда.
Исходные данные для определения процента годной продукции и требуемой точности настройки раскряжевочной установки.
Таблица 3.1
Номер наблюдения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Длины сортиментов, см |
714 |
690 |
712 |
711 |
710 |
707 |
701 |
709 |
681 |
701 |
Номер наблюдения |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Длины сортиментов, см |
687 |
704 |
701 |
708 |
699 |
688 |
686 |
702 |
703 |
693 |
Номер наблюдения |
21 |
22 |
23 |
24 |
25 |
|
|
|
|
|
Длины сортиментов, см |
675 |
709 |
704 |
688 |
707 |
|
|
|
|
|
Заданные в виде простого статистического ряда длины сортиментов распологаем в виде неубывающей последовательности, т.е. строим вариационный ряд.
Таблица 3.2
Номер наблюдения |
|
|
|
Номер наблюдения |
|
|
|
1 |
675 |
-24,1 |
605,16 |
14 |
703 |
3,4 |
11,56 |
2 |
681 |
-18,6 |
345,96 |
15 |
704 |
4,4 |
19,36 |
3 |
686 |
-13,6 |
184,96 |
16 |
704 |
4,4 |
19,36 |
4 |
687 |
-12,6 |
158,76 |
17 |
707 |
7,4 |
54,76 |
5 |
688 |
-11,6 |
134,56 |
18 |
707 |
7,4 |
54,76 |
6 |
688 |
-11,6 |
134,56 |
19 |
708 |
8,4 |
70,56 |
7 |
690 |
-9,6 |
92,16 |
20 |
709 |
9,4 |
88,36 |
8 |
693 |
-6,6 |
4,56 |
21 |
709 |
9,4 |
88,36 |
9 |
699 |
-0,6 |
0,36 |
22 |
710 |
10,4 |
108,36 |
10 |
701 |
1,4 |
1,96 |
23 |
711 |
11,4 |
129,96 |
11 |
701 |
1,4 |
1,96 |
24 |
712 |
12,4 |
153,96 |
12 |
701 |
1,4 |
1,96 |
25 |
714 |
14,4 |
207,36 |
13 |
702 |
2,4 |
5,76 |
Итого |
17490 |
— |
2718 |
С помощью t-критерия Стьюдента исключаем из вариационного ряда анормальные результаты наблюдений. Для этого вычисляем:
Выборочное
среднее:
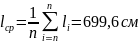 ;
;
Выборочную
дисперсию:
 ;
;
Выборочное
среднеквадратическое отклонение:
 ;
;
Расчетный t-критерий:
 ;
;
 .
.
По
числу степеней свободы
 ,
принятому уровню значимости
,
принятому уровню значимости
 определяем t-критерий
Стьюдента. Если
определяем t-критерий
Стьюдента. Если
 и
и
 ,
то гипотеза отвергается, значения
,
то гипотеза отвергается, значения
 и
и
 признаются анормальными и исключаются
из выборки. Проверку такого рода
необходимо производить до тех пор, пока
не выполнится условие:
признаются анормальными и исключаются
из выборки. Проверку такого рода
необходимо производить до тех пор, пока
не выполнится условие:
 и
и
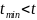 .
.
 — условие
выполняется.
— условие
выполняется.
 — условие
не выполняется.
— условие
не выполняется.
Располагаем результаты в виде вариационного ряда.
Таблица 3.3
Номер наблюдения |
|
|
|
Номер наблюдения |
|
|
|
1 |
681 |
-19,63 |
385,3369 |
14 |
704 |
3,37 |
11,3569 |
2 |
686 |
-14,63 |
214,0369 |
15 |
704 |
3,37 |
11,3569 |
3 |
687 |
-13,63 |
185,7769 |
16 |
707 |
6,37 |
40,5769 |
4 |
688 |
-12,63 |
159,5169 |
17 |
707 |
6,37 |
40,5769 |
5 |
688 |
-12,63 |
159,5169 |
18 |
708 |
7,37 |
54,3169 |
6 |
690 |
-10,63 |
112,9969 |
19 |
709 |
8,37 |
70,0569 |
7 |
693 |
-7,63 |
58,2169 |
20 |
709 |
8,37 |
70,0569 |
8 |
699 |
-1,63 |
2,6569 |
21 |
710 |
9,37 |
87,7969 |
9 |
701 |
0,37 |
0,1369 |
22 |
711 |
10,37 |
107,5369 |
10 |
701 |
0,37 |
0,1369 |
23 |
712 |
11,37 |
129,2769 |
11 |
701 |
0,37 |
0,1369 |
24 |
714 |
13,37 |
178,7569 |
12 |
702 |
1,37 |
1,8769 |
Итого |
16815 |
— |
2087,626 |
13 |
703 |
2,37 |
5,6169 |
|
|
|
|
С помощью t-критерия Стьюдента исключаем из вариационного ряда анормальные результаты наблюдений. Для этого вычисляем:
Выборочное среднее:
 ;
;
Выборочную дисперсию:
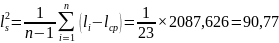 ;
;
Выборочное среднеквадратическое отклонение:
 ;
;
Расчетный t-критерий:
 ;
;
 .
.
По числу степеней свободы , принятому уровню значимости определяем t-критерий Стьюдента. Если и , то гипотеза отвергается, значения и признаются анормальными и исключаются из выборки. Проверку такого рода необходимо производить до тех пор, пока не выполнится условие: и .
 — условие
выполняется.
— условие
выполняется.
 — условие
выполняется.
— условие
выполняется.
Для построения гистограммы, определяем числа разрядов (интервалов), для которых вычислим относительные или абсолютные частоты (количество попаданий той или иной случайной величины в интервал).
Определяем
число интервалов по формуле:

Шаг
интервала определяем по формуле:

Полученные данные сводим в таблицу.