8. Механической характеристик асинхронного двигателя

Холостого хода

М=0

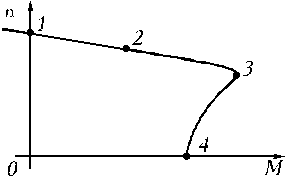ω=ω₀=104,5 рад/с

Номинальная

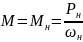
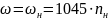
Критическая

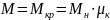
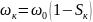
Минимальная

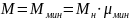
Пусковая

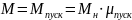
9. Кинематическая схема электропривода

  Непосредственное представление о механических связях даёт кинематическая схема электропривода (рис. 2.2):

Рис. 2.2. Кинематическая схема электропривода

  Здесь двигатель Д через соединительную муфту СМ1, клиноременную передачу (КРП), ряд зубчатых передач ЗПi и соединительную муфту СМ2 приводит во вращение барабан (Б), преобразующий вращательное движение в поступательное движение ряда связанных масс. При нагружении элементы системы (валы, опоры, клиноременные передачи, зубчатые зацепления и т.п.) деформируются, т. к. механические связи не являются абсолютно жёсткими. При изменении нагрузки массы имеют возможность взаимного перемещения, которое определяется жёсткостью связи.

  Каждый вращательно движущийся элемент обладает моментом инерции Ji и связан с (i+1) - элементом механической связью, обладающей жёсткостью Ci. Соответственно каждый поступательно движущийся элемент имеет массу mj и связан со следующим связью с жёсткостью Сj. В пределах механических связей, для которых выполняется закон Гука, жёсткости можно определить с помощью соотношений

      (2.1)

где

    - нагрузка упругой механической связи;

     - деформация упругого элемента при вращательном и поступательном движении.

  В связи с наличием передач различные элементы системы движутся с различными скоростями. Поэтому для составления расчетных схем необходимо приведение всех параметров элементов кинематической цепи к одной расчётной скорости, обычно к скорости вала двигателя.

  Условием соответствия расчётной схемы реальной механической системе является выполнение закона сохранения энергии. При приведении необходимо обеспечить сохранение кинетической и потенциальной энергий системы, а также элементарной работы всех действующих в системе сил и моментов на возможных перемещениях. Следовательно,

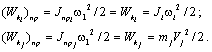      (2.2)

  Отсюда получаем формулы приведения:

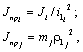      (2.3)

где

     - передаточное число от вала приведения до i-го вала;

     - радиус приведения к валу со скоростью ω 1 .

  При приведении вращательных φi и поступательных Sj перемещений необходимо учитывать, что передаточное число и радиус приведения определяются соотношением скоростей. Тогда перемещения связаны зависимостями:

  При линейных кинематических связях   . В этом случае формулы приведения перемещений имеют вид:

  При приведении жёсткостей механических связей должно выполняться условие равенства запаса потенциальной энергии деформации.

  Потенциальная энергия Wn равна работе, совершаемой моментом М на участке изменения угла Δφ. Так как величина момента скручивания изменяется от 0 до Mmax, то, с учетом (2.1), работа равна:

  Тогда

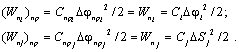
  Формулы приведения:

      (2.4)

  Приведение моментов и сил нагрузки элементов кинематической цепи должно осуществляться при условии равенства элементарной работы на возможных перемещениях:

  Следовательно,

      (2.5)

  Для большей наглядности сопоставления по результатам приведения можно построить исходную приведённую расчётную схему, представив в ней массы в виде прямоугольников, площадь которых пропорциональна приведенным моментам инерции, а жёсткости связей между ними в виде соединений, длина которых обратно пропорциональна жёсткости.