3. Введение в математический анализ

3.1. Основные понятия функции одной переменной

Зависимость переменной у от переменной х называется функцией, если каждому значению х по некоторому правилу f поставлено в соответствие единственное значение у. Переменную х называют независимой переменной или аргументом, а переменную y – зависимой переменной. Значение у, соответствующее заданному значению х, называют значением функции. Записывают: у=f(х) (читается: «игрик равен эф от икс»). Буквой f обозначается функциональная зависимость между переменными х и у. Говорят также, что f(х) есть значение функции в точке х.

Все значения независимой переменной х, при которых функция f(х) имеет смысл, образуют область определения функции D(y).

Все значения, которые принимает функция f(х) на области ее определения, образуют область значений функции Е(у).

Например, функция у=sin(x) определена для любого значения аргумента х, т.е. область определения функции D(y): x(–; ). При этом значения этой функции размещаются на отрезке от –1 до 1. Говорят, что область значений функции Е(у): y[–1; 1].

Графиком функции называется множество всех точек плоскости, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции.

Значение функции при называется частным значением функции в точке и обозначается .

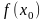Пример 1. Вычислить значение функции при .

Решение. Частное значение данной функции в точке равно .

Пример 2. Вычислить значение функции

при а) х= –3; б) х=2; в) х=4.

Решение. а) Так как , то . Поэтому частное значение функции равно .

б) . Поэтому 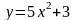и частное значение функции равно .

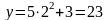в) В данном случае 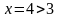. Следовательно, у=1.

Можно выделить случаи, когда область определения функции не совпадает со всей числовой прямой:

1) если , то D(y): определяется неравенством f(x)0;

2) если 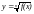(n– чётное), то D(y): определяется неравенством f(x)0;

3) если (а>0, a1), то D(y): определяется нера­венством f(x)>0;

4) если 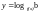(b>0), то D(y): определяется системой неравенств ;

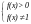5) если , то то D(y): определяется неравенством |f(x)|≤1;

если 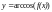, то то D(y): определяется неравенством |f(x)|≤1.

Пример 3. Найти область определения следующих функций:

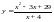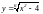a) ; б) ; в) .

a) Функция определена в том случае, если знаменатель х+4 не обращается в 0, т.е х+40. Решая это неравенство, получим х – 4.

Этому неравенству удовлетворяют все значения переменной х числовой оси Ох, кроме точки – 4.

Поэтому D(y): x(–; –4) U(–4; ).

б) Функция определена в том случае, если подкоренное выражение неотрицательно, т.е. . Для решения этого неравенства найдем точки пересечения графика функции у=х²–4 с осью Ох, для чего приравняем левую и правую части неравенства и получим уравнение 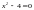. Решением этого уравнения являются точки х₁= –2 и х₂= 2. Тогда, решая исходное неравенство методом парабол, получим

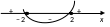
D(y): x(–; –2] U[2; ).

в) Функция определена только для тех значений переменной х, которые удовлетворяют неравенству 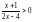, которое можно переписать в виде

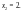Найдём точки пересечения графика функции с осью Ох из уравнения . Произведение двух сомножителей равно 0, если хотя бы один из них обращается в 0, т.е. уравнение разобьется на два простейших или , решениями которых являться точки и Тогда, применив для исходного неравенства методом интервалов, получим:

D(y): x(–; –1) U(2; ).