1.6. Еквівалентність процентних ставок

Для банку, який облікує вексель на суму грошей S, облікова вартість векселя є теперішньою вартістю суми грошей S, тобто це сума, яку банк виплатить пред’явнику векселя, а D – дисконт, сума, яку банк отримує з векселеотримувача в момент погашення, тобто через термін t, що залишився до погашення.

На відміну від звичайної ситуації, коли інвестується відома сума грошей, на яку за час t нараховуються проценти за процентною ставкою (і), що називається ставкою процентів, при обліку наперед відомо нарощену суму, а її поточну вартість знаходимо з урахуванням облікової ставки (d) і терміну, який залишився до погашення. Таким чином, дисконт та дисконтна (облікова) ставка є такими ж характеристиками кредитної угоди, як процент і процентна ставка. Вони відрізняються лише напрямком схеми розрахунку. При обчисленні процентів та ставки процентів основною (вихідною) величиною є початкова (поточна) вартість, а при обчисленні дисконту й облікової ставки - майбутня сума грошей.

Розглянемо схему:

Рис. 6.

Проценти за період t = t₂ – t₁

дорівнюватимуть I = S – P.

Процентна ставка за цей період i_t =

З іншого боку, дисконт за цей період D_t = S – P = I_t,

а облікова ставка за період:

d_t = .

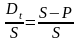Ми бачимо, що ставка процентів та облікова ставка пов’язують наступні суми P та S, які відносяться до початку та кінця періоду t.

З формули (1.7)

P = S ´ (1 – d_t),

маємо

S = .

З формули (1.3)

S = P ´ (1 + i_t).

Із отриманих рівностей випливає, що

(1 + i_t) ´ (1 – d_t) = 1,

або рівність множників нарощення та дисконтного

1 + i_t = .

З отриманої рівності отримуємо формули:

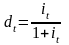(1.9)

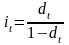(1.10)

Нехай i_t та d_t - прості (ставка процентів та облікова ставка) і відповідають річним обліковій та процентній ставкам i та d, тобто

i_t = i ´ t, d_t = d ´ t,

тоді для терміну 1 рік (t = 1) отримаємо співвідношення:

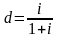(1.9')

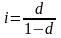(1.10')

Співвідношення (1.9') та (1.10') дають можливість такої інтерпретації дисконту. Нехай на початок року інвестується одинична сума грошей за ставкою процентів i. Тоді на кінець року проценти становитимуть суму i, а поточне значення цієї величини дорівнюватиме:

.

Із рівності (1.10') маємо:

(1 – d) i = d.

Отже, дисконт – це проценти, які виплачуються не наприкінці року (періоду), а на початку. Тому іноді дисконтну ставку називають авансованою процентною ставкою.

У фінансових розрахунках треба навчитися розрізняти ставку процентів та облікову ставку. Вони характеризують кредитну угоду по-різному. Різниця між ними - у виборі часової бази, а саме - моменту часу, щодо якого обчислюється вигідність кредитної угоди (фінансової операції). Для ставки процентів це - початок терміну угоди, а для облікової ставки - кінець терміну угоди. Вищезазначені формули дають змогу знайти для довільної із заданих величин другу величину для одного і того ж періоду часу.

Кажуть, що ці формули задають умови еквівалентності облікової та ставки процентів стосовно заданого періоду часу.

ВИЗНАЧЕННЯ. Різні за видом процентні ставки називаються еквівалентними, якщо в однотипних фінансових операціях вони дають у розрахунках однакові остаточні результати.

З формули (1.7')

P = S ´ (1 – d ´ t)

випливає ще один метод обчислення теперішньої вартості, використовуючи облікову ставку. Якщо ж і - відповідна еквівалентна для періоду часу t ставка процентів, тоді формула (1.4)

P =

дає такий же результат. Отже, еквівалентність і та d означає, що

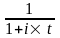= 1 – d ´ t.

ПРИКЛАД 14. Знайти теперішню вартість 200 грн., отриманих через два роки:

а) при ставці процентів 10,5 %; б) за обліковою ставкою 10,5 %.

Дано: S = 200 грн. d = 0,105 %. t = 2 p.	РОЗВ’ЯЗОК б) для облікової ставки 10,5 %: за формулою (1.7) P = S ´ (1 –– d ´ t) = 200 ´ 0,79 = 158 (грн.)
P - ?

Дуже важливо пам’ятати про те, що про еквівалентність або відповідність ставки процентів та облікової ставки можна говорити лише тоді, коли вказано термін, щодо якого стверджується еквівалентність. Ставки, які еквівалентні стосовно одного фіксованого періоду часу, не будуть еквівалентними щодо іншого періоду часу.

ПРИКЛАД 15. Нехай проста річна ставка становить 20 %. Знайти еквівалентні річні облікові ставки для термінів:

а) три місяці; б) півроку.

а)

Дано: i = 0,2 t =	РОЗВ’ЯЗОК якщо d - відповідна річна облікова ставка, тоді з рівняння еквівалентності: dt = отримаємо, що d = 19 %.
d - ?

б)

Дано: i = 0,2 t = 1/2	РОЗВ’ЯЗОК d = = 0,1818; d = 18 %.
d - ?

Побудуємо графіки залежностей

d = d (i) та i = i (d) для терміну один рік:

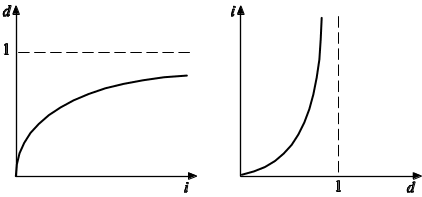
Рис. 7.