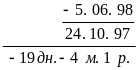1.2. Звичайні, точні та комерційні проценти
У попередніх розглянутих прикладах термін інвестування виражався в роках, місяцях. Іноді задають його також календарними датами першого та останнього днів інвестування. Тоді, щоб використовувати формулу простих процентів, спочатку треба визначити загальну кількість днів інвестування позики, а потім виразити термін як частину року, склавши відношення кількості днів користування грошима і кількості днів у році, тобто:
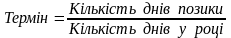
Це буде формула:
,
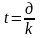де k - к-сть днів у році;
д - к-сть днів інвестування (позики);
t - термін інвестування у роках.
Існує два методи обчислення кількості днів позики - точний і наближений. При цьому виключається перший або останній день терміну.
І метод. Точна кількість днів обчислюється з використанням таблиці (Додаток 1 «Порядкові номери днів у році») або за допомогою календаря року.
Нехай:
дв - день початку терміну інвестування, або дата видачі позики,
дп - день закінчення терміну, або дата погашення позики.
Тоді:
д = дп – дв – для звичайного року,
та д = дп – дв + 1 – для високосного року, за умови, що 29 лютого входить у термін інвестування.
ПРИКЛАД 5.
Знайти точну кількість днів між 3 березня та 30 вересня.
РОЗВ’ЯЗОК.
У Таблиці 1 (Додаток 1) знаходимо, що 29 вересня - це 272-й день, а 3 березня 62-й день року.
Отже, точне число днів між датами: 272 – 62 = 210 (днів).
ІІ метод: Наближений метод вираховує наближене число днів, виходячи із повної кількості місяців у терміні та числа днів неповного місяця. При цьому вважають, що місяць має 30 днів. Від дати погашення віднімають дату видачі позики і переводять кількість місяців у дні, які отримані при відніманні дат (якщо отримано від’ємну кількість днів – їх віднімають).
ПРИКЛАД 6.
Знайти наближене число днів між 3 березня та 30 вересня.
Дано: дв = 3.03 дп = 30.09
|
РОЗВ’ЯЗОК
Між датами – повних 6 місяців (від 3 березня до 3 вересня) та залишається ще 27 днів (від 3 березня до 30 вересня). Отже, число днів між заданими датами: (6 ´ 30) + 27 = 207 (ддніів). |
д - ? |
|
Якщо дата початку інвестування (дата видачі позики) та його завершення (дата погашення) - у різних роках, тоді методика обчислення наближеної кількості днів не змінюється (рік при цьому перетворюють у дні, з розрахунку, що у ньому - 360 днів), а методика точного нарахування днів інвестування трохи видозмінюється, проілюструємо це на прикладі 7.
ПРИКЛАД 7.
Знайти наближену та точну кількість днів, якщо дата видачі - 24 жовтня 1997 року, а дата погашення - 5 червня 1998-го.
Дано: дв = 24.10.1997 рр. дп = 5.06.1998 рр. |
РОЗВ’ЯЗОК а) наближена кількість днів:
днааблл. = 360 –– (4 ´ 30) –– 19 = 221 (день); |
дтоочнн. - ? днааблл. - ? |
|
Наведені вище методики наближеного та точного обчислення кількості днів інвестування дозволяють розглянути кілька способів обчислення простих процентів за формулою:
(1.1¢)
Якщо термін інвестування менший року, тобто , тоді при різних значеннях д і k можна отримати такі результати:
Якщо д - наближена кількість днів інвестування, k = 360, то обчислені за формулою (1.1') прості проценти називають звичайними.
У світовій фінансовій практиці цей метод обчислення простих процентів називають німецьким.
Якщо д - точна кількість днів інвестування, k = 360, то обчислені проценти за формулою (1.1') називаються комерційними, а метод обчислення - французьким.
Якщо д - точна кількість днів інвестування, k = 365 (366), то обчислені проценти називають точними, а метод - англійським.
Найпоширеніший у фінансовій практиці - комерційний метод нарахування простих процентів. Він вигідний інвестору. Для боржника вигідний точний метод нарахування простих процентів. Його використовують при міжнародних валютних операціях.