3.5. Рівняння еквівалентності з невідомою кількістю виплат
Ми бачимо, що рівняння еквівалентності включає такі фактори: величину виплати, термін виплати, еквівалентне значення для множини виплат на термін, який відповідає цьому значенню, процентна ставка. У попередніх прикладах у рівнянні еквівалентності невідомим параметром було еквівалентне значення. У багатьох випадках виникає необхідність знаходження терміну виплати чи процентної ставки, або іншого параметра, який входить у рівняння еквівалентності.
Для обґрунтування вищесказаного розглянемо приклади:
ПРИКЛАД 6.
Борг необхідно погасити двома платежами - 70 тис. гривень через два роки та 230 тис. гривень - через чотири роки. Знайти термін, коли заміна обох виплат однією виплатою розміром 250 тис. гривень буде еквівалентною, за річною процентною ставкою 15 %.
Розв’язок.
Часова схема виплат для нашого випадку є такою (рис. 20):
Рис. 20.
Нехай n - шуканий термін виплати 250 тис. гривень. Запишемо рівняння еквівалентності для сьогоднішнього моменту часу t = 0.
250 000 ´ (1,15)-n = 70 000 ´ (1,15)-2 + 230 000 ´ (1,15)-4.
Звідси ми маємо
n
=
(року).
У разі, коли потік платежів замінюють однією виплатою, яка дорівнює сумі цих платежів, тоді дата, яка відповідає вказаній виплаті, що є еквівалентна множині платежів, називається середнім терміном.
ПРИКЛАД 7.
Для послідовності із трьох виплат 30 тис. гривень сьогодні, 60 тис. гривень через три роки, 100 тис. гривень через шість років знайти середній термін (дату), коли ця послідовність виплат буде еквівалентною 200 тис. гривень. Проценти нараховуються за ставкою 10 % річних.
Розв’язок.
Часова діаграма виплат буде такою:
Рис. 21.
де n - середній час виплати.
Випишемо рівняння еквівалентності для сьогоднішнього моменту часу t = 0:
200 000 ´ (1,1)-n = 30 000 + 60 000 ´ (1,1)-3 + 100 000 ´ (1,1)-6.
З останнього рівняння отримаємо:
n
=
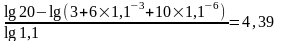(року).
Слід зауважити, що розв’язок рівняння еквівалентності щодо середнього терміну, з математичного погляду, не є важким. Однак якщо вимагається отримати лише грубе наближення, тоді можна скористатися такою формулою:
n
=
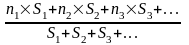(3.2)
У цій формулі Sk означає виплати, які відповідають періодам nk нарахування процентів, k = 1, 2, .......
ПРИКЛАД 8.
Для послідовності із шести виплат (50 грн. сьогодні, 90 грн. - через три місяці, 190 грн. - через п’ять місяців, 110 грн. - через сім місяців, 150 грн. - через вісім місяців та 120 грн. - через рік) оцінити середній термін, за умови, що проценти становлять 3 % місячних.
Розв’язок
Нехай n - середній час виплати. Тоді за формулою (3.2) наближеного обчислення виплати
n
=
.
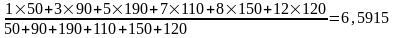Середній час виплати - 6,59 місяця, або 198 днів.
Завдання для самоконтролю по III розділу
Знайти еквівалентне за ставкою 11 % річних значення суми 21000 гривень, яку слід сплатити через рік для таких моментів часу: а) сьогодні; б) через три роки; в) через сім років; г) через десять років.
Знайти еквівалентне через три роки значення для боргу, який дорівнює 400 гривень сьогодні при щоквартальному нарахуванні процентів за ставкою 24 % річних.
Для послідовності з п’яти виплат розміром 50 гривень кожна з очікуваних через місяць, два місяці, чотири місяці, півроку та дев’ять місяців знайти еквівалентне значення за ставкою 15 % річних: а) через рік; б) через 1,5 року; в) через 3 роки.
Борг треба виплатити двома платежами: 60 гривень у кінці другого року та 300 гривень у кінці п’ятого року. Знайти еквівалентну цим виплатам суму одноразового платежу при нарахуванні процентів за ставкою 8% річних: а) сьогодні; б) наприкінці другого року; в) наприкінці четвертого року;
Порівняти два боргових зобов’язання:
1) борг становить 300 гривень плюс складні проценти за ставкою 15 % річних. Термін погашення - 3 роки;
2) борг становить 180 гривень плюс складні проценти за ставкою 9 % річних при нарахуванні два рази на рік. Термін погашення - 3 роки.
Замінити такий потік платежів: 80 гривень - через рік, 100 гривень - через два роки, 90 гривень - через три роки, 150 гривень - через п’ять років, еквівалентним потоком із двох рівних за величиною виплат: перша - через півтора року; друга - через п’ять років. Проценти нараховують за ставкою 6 % річних кожних півроку.
Борг треба погасити двома платежами: 100 гривень - через рік та 400 гривень через три роки. За процентною ставкою 14 % річних знайти час, коли заміна обох виплат однією виплатою розміром 510 гривень буде еквівалентною (рівнозначною).
Для потоку платежів із трьох виплат (150 гривень - сьогодні; 300 гривень - через два роки; 450 гривень - через п’ять років) знайти середній термін, користуючись точним і наближеним методами. Проценти становлять 16 % річних.