
- •Передмова
- •I. Прості проценти та їх застосування у фінансовій практиці
- •1.1. Обчислення простих процентів
- •1.2. Звичайні, точні та комерційні проценти
- •1.3. Теперішня вартість
- •1.4. Короткострокові боргові зобов’язання
- •1.5. Облікова ставка і дисконт
- •1.6. Еквівалентність процентних ставок
- •1.7. Врахування інфляції у короткострокових фінансових операціях
- •1.8. Застосування простих процентів у споживчому кредиті
- •Завдання для самоконтролю по I розділу
- •II. Фінансові обчислення на основі складних процентів
- •2.1. Капіталізація складних процентів
- •2.2. Номінальна та ефективна ставки процентів
- •Приклад 3.
- •2.3. Неперервні проценти
- •2.4. Дисконтування за складними процентними ставками
- •Визначення теперішньої та майбутньої вартості грошей для довільного терміну
- •2.6. Обчислення термінів інвестування та процентних ставок
- •2.7. Вимірювання ефективності позикових та облікових операцій
- •Приклад 16.
- •2.8. Врахування інфляції у довгострокових фінансових операціях
- •Завдання для самоконтролю по II розділу
- •III. Фінансова еквівалентність Рівняння еквівалентності
- •3.1. Еквівалентність платежів
- •3.2. Рівняння еквівалентності
- •3.3. Нееквівалентні платежі
- •3.4. Еквівалентність потоків платежів
- •3.5. Рівняння еквівалентності з невідомою кількістю виплат
- •Завдання для самоконтролю по III розділу
Визначення теперішньої та майбутньої вартості грошей для довільного терміну
У практичних задачах термін інвестування не завжди є цілим числом періодів нарахувань процентів. Для обчислення нарощеної (майбутньої) або теперішньої вартості грошей у такому разі цілком логічно знайти процентну ставку, еквівалентну вихідній ставці, при якій термін дорівнюватиме цілому числові періодів нарахувань.
ПРИКЛАД 11
16 тис. грн. інвестовано на 1 рік та 5 місяців під складні проценти за ставкою 15 % річних. Знайти нарощену суму грошей на кінець терміну.
Дано: P = 16 тис. грн. n = 1 р. 5 міс. іc = 15 % |
Розв’язок Знайдемо процентну ставку j12, яка відповідає нарахуванню процентів щомісяця і при цьому еквівалентна 15 % річних. За формулою (2.5) обчислюємо: (1 + j12)12 = (1 + 0,15). Звідси місячна ставка процентів:
j12
=
|
S = ? |
j12 = 11,7 %. |
Отож, нарощена сума за формулою (2.1) дорівнюватиме:
S = 16 000 ´ (1 + 0,0117)17 = 16 187,43 (грн.)
Зауважте, що в наведеному прикладі
(1 + 0,0117)17 = (1 + 0,15)17/12.
Ця рівність справедлива й у загальному випадку. Таким чином, обчислена за формулою складних процентів нарощена або теперішня вартість не залежить від того, чи термін інвестування є цілим числом періодів, чи не є. Результат такий же, як і при обчисленні з використанням еквівалентної ставки.
У зв’язку із трудомісткими обчисленнями, які виникають при ірраціональному терміні, здебільшого використовують наближені методи, які цілком задовольняють необхідну точність обчислень. Одним із найпоширеніших методів є так званий банківський метод, при якому на повне число періодів нараховують складні проценти, а на залишок часу - прості проценти.
Позначимо na - повне число років;
nb - дробову частину року,
тоді n = na + nb.
У цьому разі множник нарощення складних процентів дорівнює:
(1
+ i)n
= (1 + i)na
+ nb
= (1 + i)na
´
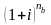 .
.
На практиці множник заміняють наближеним його значенням (1 + i ´ nb). Тоді формула (2.1) набуде вигляду:
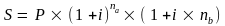 (2.11)
(2.11)
ПРИКЛАД 12.
Борг у розмірі 160 тис. грн. треба виплатити через 2 роки і 5 місяців. Знайти теперішню вартість боргу за умови, що проценти за кредит нараховуються за ставкою 15 % річних.
Дано: Р = 160 тис. грн. n = 2 роки і 5 місяців і = 15 % |
РОЗВ’ЯЗОК З формул (2.7) та (2.11) маємо
Р
= |
S = ? |
|
2.6. Обчислення термінів інвестування та процентних ставок
Будемо вважати, що суму грошей Р виплачують у момент часу n, а суму грошей S виплатять у момент часу t + n. У даному разі n - термін між виплатами. Він виражається у фіксованих періодах, а саме - роках, місяцях, днях. Постає проблема знаходження ефективної процентної ставки за період, упродовж якого ці суми еквівалентні.
Розв’язавши рівняння (2.1) S = P ´ (1 + i)n, знайдемо складну ставку:
 (2.12)
(2.12)
Якщо n - термін між виплатами P i S у роках, тоді для номінальної річної ставки, яка відповідає m-кратному нарахуванню процентів у році, з формули (2.2) S = P ´ , замінивши t на n, отримаємо
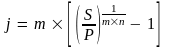 (2.13)
(2.13)
Неперервну процентну ставку знаходимо з формули (2.8):
 ,
,
замінивши t на n:
j
=
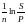 (2.14)
(2.14)
ПРИКЛАД 13
Знайти процентну ставку для кредиту в 200 тис. грн. Сума при погашенні становить 350 тис. грн. Кредит видано на 3 роки. Вважаємо, що процентна ставка є:
1) річною; 2) неперервною.
Дано: P = 200 тис. грн. S = 350 тис. грн. n = 3 |
РОЗВ’’ЯЗОК 1) ЗЗа ффоррмуулоою (2.12) рріччнаа сстаавкка:
i
= |
i1 - ? i2 - ? |
2) За формулою (2.14) неперервна ставка: j
=
|
Найпоширенішим методом наближених обчислень процентних ставок є метод лінійної інтерполяції. При цьому рівняння S = P ´ (1+i)n розв’язується стосовно множника нарощення:
а
=
(1 + і)n;
a
=
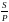 .
.
Пізніше
у Таблиці
2 (Додаток
2)
знаходимо для згаданого терміну дві
процентні ставки
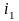 та
та
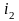 ,
які відповідали б виразові:
,
які відповідали б виразові:
а1
=
(1 +
)n
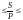 (1+
)n
=
а2.
(1+
)n
=
а2.
При цьому а1 та а2 є наближчими верхнім та нижнім значеннями а. Наближене значення шуканої процентної ставки і випливає з лінійного рівняння:
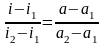 (2.15)
(2.15)
ПРИКЛАД 14
Обчислити прибутковість інвестиції, яка характеризується місячною процентною ставкою. Початкова сума інвестиції становить 200 тис. грн., а нарощена сума становитиме 250 тис. грн. Термін інвестування - 5 місяців.
Дано: P = 200 тис. грн. S = 250 тис. грн. n = 5 міс. |
РОЗВ’ЯЗОК Нехай і - шукана місячна процентна ставка.
Тоді
а
=
a
|
i - ? |
|
За Таблицею 2 (Додаток 2) знайдемо нижню та верхню границі для заданого значення а = 1,25 при 5-місячному терміні інвестування та відповідні їх процентні ставки.
= 4 % а1 = 1,2167
= 5 % а2 = 1,2763
1,2167
< 1,25
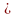 1,2763
1,2763
Підставимо отримані значення у формулу (2.15):
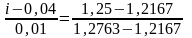
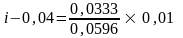 .
.
Звідси
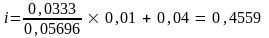 .
.
Отож, прибутковість інвестицій становитиме 4,56 %.
Для визначення терміну, на який інвестовано грошову суму Р під складні проценти за ставкою і та на фіксований період часу n з метою нагромадження суми грошей S до кінця згаданого періоду, скористаємося формулою S = P ´ (1 + i)n. З неї випливає, що термін n виражається формулою:
n
=
 (2.16)
(2.16)
Слід пам’ятати, що період n виражається узгоджено із відповідним періодом процентної ставки. Скориставшись аналогічним міркуванням, можна отримати термін інвестування для неперервного нарахування процентів:
n
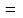
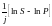 (2.17)
(2.17)
ПРИКЛАД 15.
На який термін часу треба покласти 120 тис. грн. під:
а) складні проценти за ставкою 16 % річних;
б) неперервні проценти за ставкою 6 %,
щоб наростити до кінця терміну 360 тис. грн.?
Розв’язок
а) за формулою (2.16)
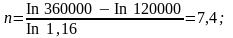
б) за формулою (2.17)
n
=
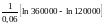 =
18,31.
=
18,31.

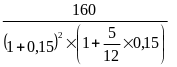 =113,86635
(тис. грн.).
=113,86635
(тис. грн.).