3. Пример 1

Вычислим с помощью метода хорд корень уравнения с точностью . Под точностью будем понимать отклонение модуля функции от нулевого значения.

Выберем в качестве левой границы отрезка . При этом . В качестве правой границы можно взять . При этом . Выполняется необходимое условие .

Найдем первое приближение корня

Найдем значение функции в этой точке

Проверим, не надо ли прекратить вычисления:

, значит, точность еще не достигнута.

Т.к. , следующим отрезком будет .

Найдем второе приближение корня

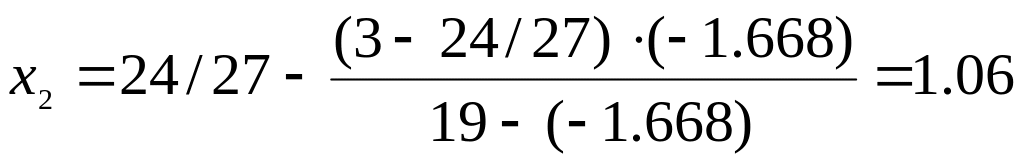
Найдем значение функции в этой точке

.

, поэтому продолжаем вычисления.

Т.к. , следующим отрезком будет

. И т.д. до достижения заданной точности.

4. Пример 2

Вычислим с помощью метода Ньютона корень уравнения с точностью .

Под точностью будем понимать отклонение модуля функции от нулевого значения.

Выберем в качестве левой границы отрезка . Значение функции в этой точке равно . В качестве правой границы можно взять . Значение функции в этой точке равно . А значит, выполняется необходимое условие применения метода .

Кроме этого выполняется требование непрерывности второй производной функции: – непрерывная функция.

А также на выбранном отрезке вторая производная функции не меняет знак. Действительно, больше нуля на всем отрезке .

Выберем в качестве первого приближения , т.к. .

Найдем второе приближение корня

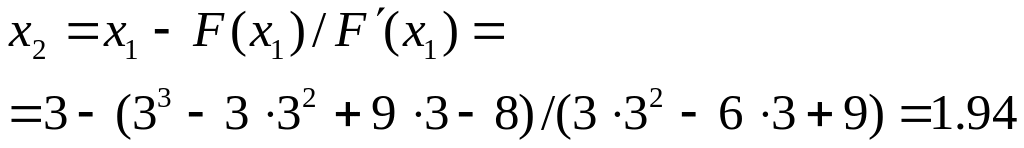
Значение функции в этой точке равно

поэтому продолжаем и ищем третье приближение корня

Значение функции в этой точке равно

поэтому продолжаем и ищем четвертое приближение корня

Значение функции в этой точке равно

.И так далее до достижения точности.

2.2. Лабораторная работа №2

Решение нелинейного уравнения методом хорд

2.2.1. Задача №1

Воспользовавшись методом хорд для нахождения корня нелинейного уравнения, вычислить коэффициент гидравлического сопротивления при течении жидкости в трубопроводе с относительной шероховатостью внутренней стенки для заданного числа Рейнольдса Re.

Универсальный закон сопротивления для развитого турбулентного течения имеет вид:

Данные по вариантам:

№ варианта	шероховатость	число Рейнольдса Re
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

2.2.2. Задача №2

Воспользовавшись методом хорд для нахождения корня нелинейного уравнения, вычислить расход дизельного топлива Q( ) плотностью и кинематической вязкостью при перекачке по участку трубопровода длиной L= 125 км, диаметром d = 514 мм и с шероховатостью внутренней стенки = 0.0005, если насосная станция работает с двумя последовательно включенными насосными агрегатами.

Уравнение баланса напоров для участка трубопровода имеет вид:

,

где и – подпор перед станцией и напор в конце участка соответственно;

a и b – коэффициенты, определяемые типом и количеством насосов;

и – высотные отметки сечений трубопровода в начале и в конце участка.

Данные по вариантам:

№ вар.	, м	, м	a, м	b,	, м	, м
1	50	30	662		100	200
2	30	50	630		200	100
3	70	30	580		50	150
4	40	60	600		120	180
5	60	40	550		180	120
6	60	30	570		80	150
7	30	50	662		120	190
8	70	30	630		50	170
9	60	40	580		180	110
10	60	30	550		50	160

2.2.3. Задача №3

Состояние реального газа может быть описано уравнением Ван-дер-Ваальса:

, где

,

,

R – универсальная газовая постоянная,

T – температура газа,

P_c – критическое давление,

T_c – критическая температура,

V – молярный объем газа.

Воспользовавшись методом деления пополам для нахождения корня нелинейного уравнения, найти молярный объем данного газа V при заданных значениях давления P и температуры T.

Величины критических параметров P_c и T_c отдельных газов приведены с следующей таблице:

газ	метан	этан	пропан	n-бутан	i-бутан	n-пентан
	190,55	305,43	369,82	408,13	425,16	469,65
	4,695	4,976	4,333	3,871	3,719	3,435

Газ	i-пентан	n-гексан
	460,39	507,35
	3,448	3,072

Задания по вариантам:

№ вар.	1	2		3		4		5	6
Газ	Метан	этан		пропан		n-бутан		i-бутан	n-пентан
Т, К	305	508		490		760		530	600
Р, МПа	2,200	3,700		1,570		1,800		1,250	2,400
№ вар.	7		8		9		10	11		12
газ	i-пентан		n-гексан		метан		этан	n-бутан		пропан
Т, К	560		720		311		620	560		540
Р, МПа	2,250		2,500		1,750		2,370	1,600		1,590

2.3. Лабораторная работа №3