
- •Надежность технических систем и ее прогнозирование
- •Лекция 1. Общие сведения
- •1.1. Основные термины и определения
- •1.1. Случайные величины и их характеристики
- •1.2. Законы распределения вероятностей
- •1.3. Классический метод обработки статистических данных и нахождения закона распределения
- •1.4. Область применения и виды методов малых выборок
- •1.5. Метод прямоугольных вкладов
- •1.6. Метод уменьшения неопределенности
- •1.7. Использование бутстреп-метода
- •1.8. Характеристики эмпирических законов распределения
- •1.9. Нахождение доверительного интервала
- •2.2. Временные понятия
- •2.3. Показатели надежности
- •2.4. Показатели безотказности
- •2.9. Надежность систем при последовательном и параллельном соединении элементов
- •2.10. Понятие резервирования
- •2.11. Нагруженный резерв
- •2.12. Раздельное резервирование
- •2.13. Отказы
- •2.14. Зависимость интенсивности отказов от времени
- •2.15. Влияние дефектных элементов и их замены на надежность
- •2.16. Вероятность безотказной работы с учетом нагрузки и несущей способности
- •Лекция 3. Прогнозирование показателей надежности
- •3.1. Общие принципы прогнозирования
- •3.2. Особенности методов оценки показателей надежности изделий на основе форсированных испытаний
- •3.3. Особенности методов оценки показателей надежности изделий на основе прогнозирования
- •3.4. Прямой экспертный метод
- •3.5. Косвенный экспертный метод
- •3.6. Прогнозирование показателей надежности
- •3.7. Оценка достоверности прогноза
- •3.8. Правило цензурирования испытаний
- •Лекция 4. Учет вопросов надежности при конструировании
- •4.1. Учет надежности при конструировании
- •4.2. Закон взаимной связи сроков службы деталей
- •4.3. Закон рационального числа сроков службы деталей
- •4.4. Закон рационального стоимостного распределения деталей по группам их сроков службы
- •4.5. Требования к срокам службы деталей
1.3. Классический метод обработки статистических данных и нахождения закона распределения
Пусть в результате
испытаний объекта получена выборка
![]() .
Требуется определить функцию распределения
вероятностей. При объеме выборки
несколько десятков и выше (
.
Требуется определить функцию распределения
вероятностей. При объеме выборки
несколько десятков и выше (![]() )
эффективным является классический
метод:
)
эффективным является классический
метод:
совокупность значений представляют в виде вариационного ряда
 ,
где
,
где
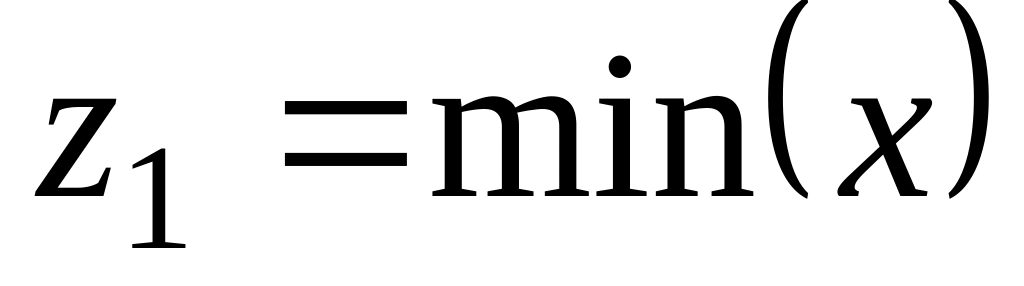 ,
,
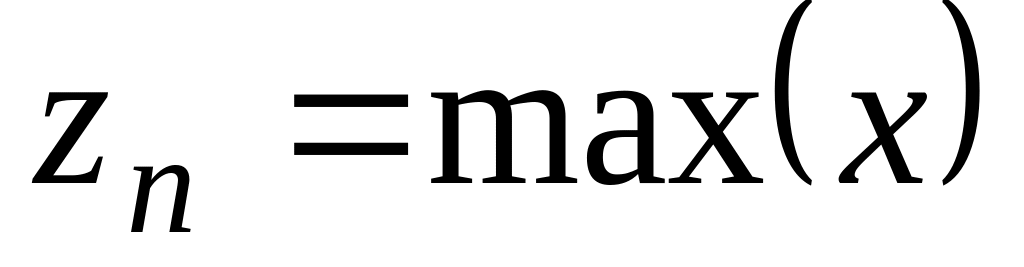 ,
т.е.
,
т.е.
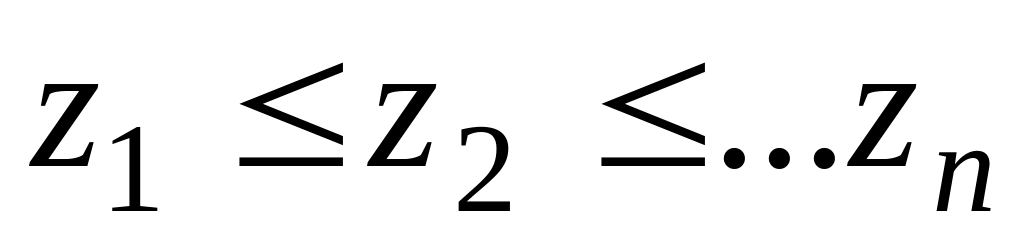 ;
;диапазон значений
 разбивают на
разбивают на
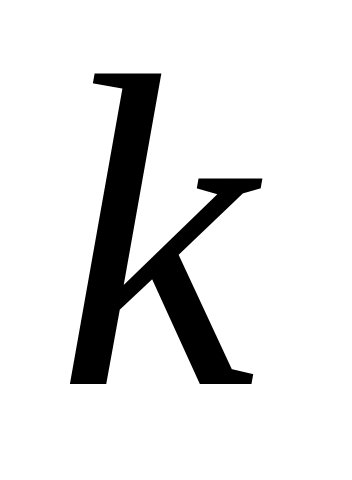 поддиапазонов. Число поддиапазонов
рекомендуется брать
поддиапазонов. Число поддиапазонов
рекомендуется брать
 .
Длина поддиапазона
.
Длина поддиапазона
![]() ;
;
вариационный ряд разбивают по поддиапазонам. В первом поддиапазоне
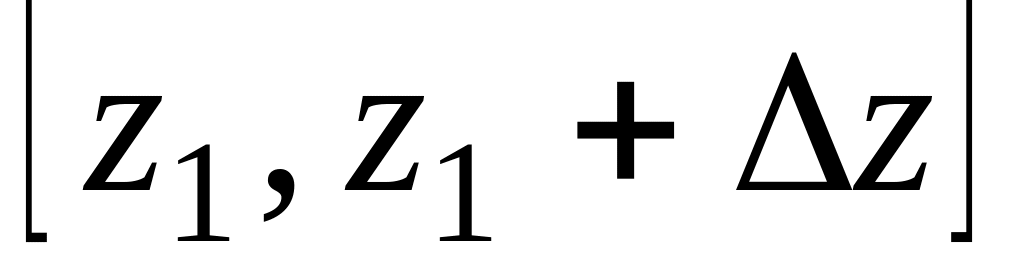 окажется
окажется
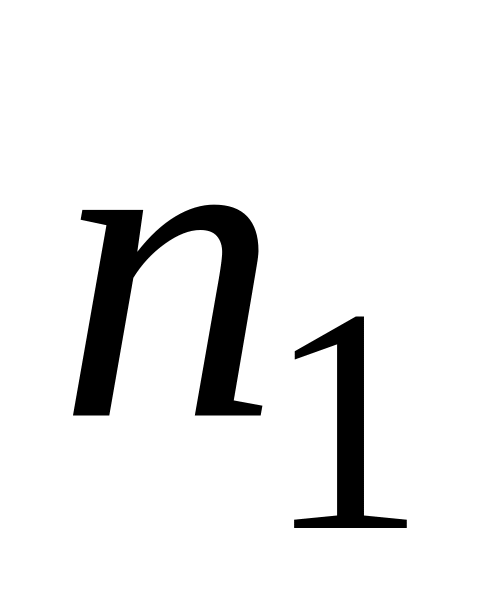 ,
во втором
,
во втором
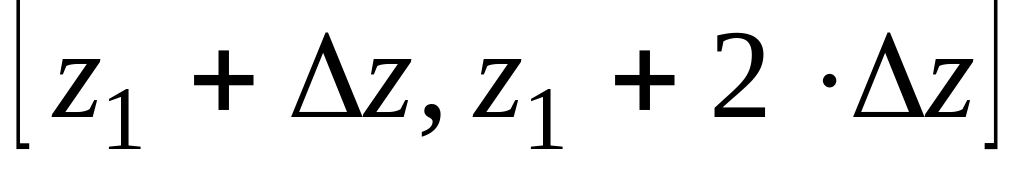 -
-
 ,
в
-м
поддиапазоне
,
в
-м
поддиапазоне
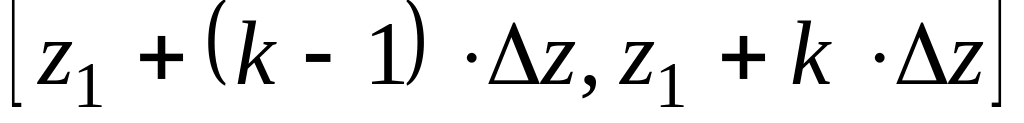 -
-
 .
Соблюдается
.
Соблюдается
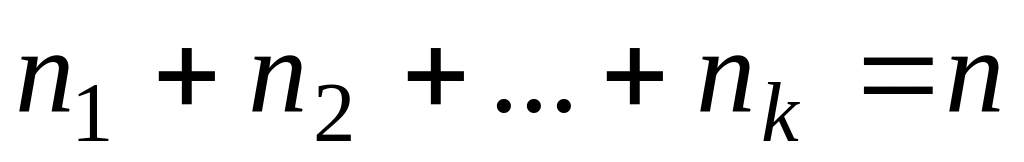 ;
;определяются частоты появления результатов в каждом поддиапазоне
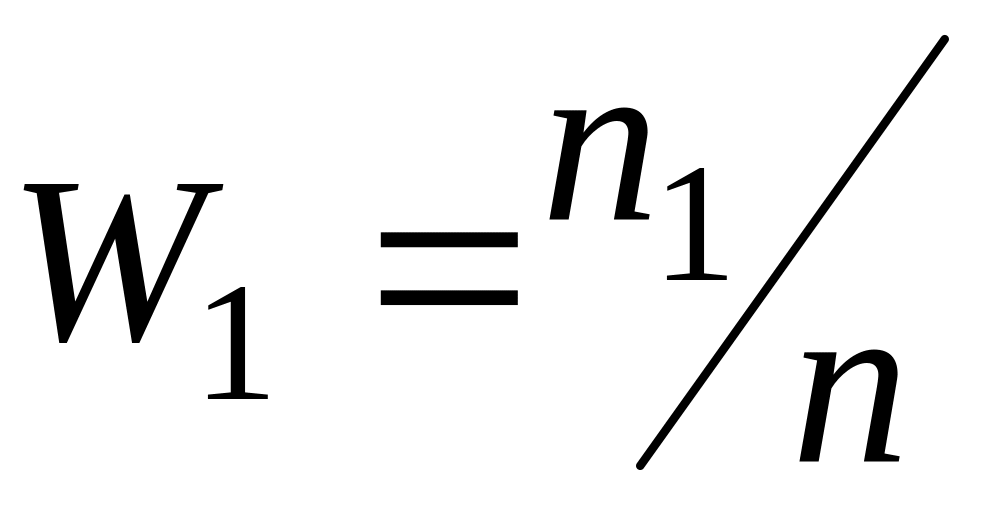 ,
,
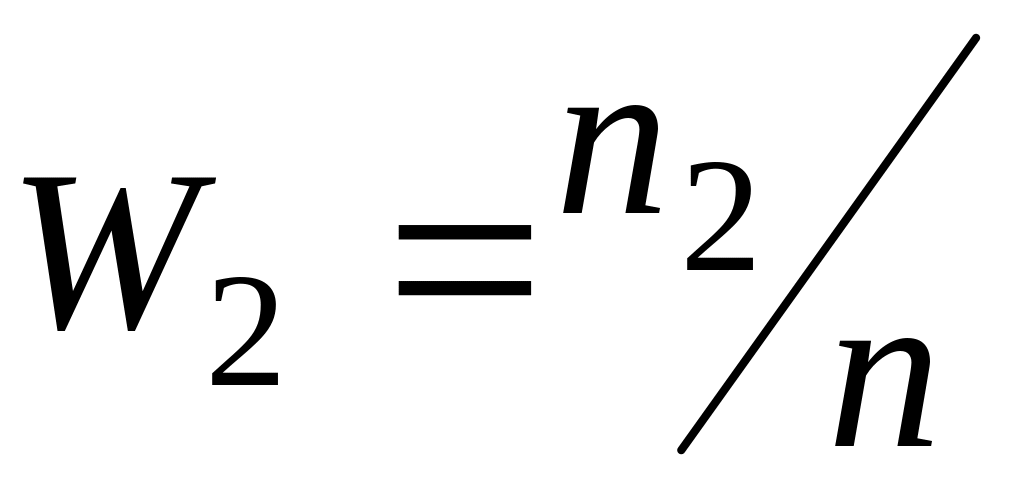 ,…
,…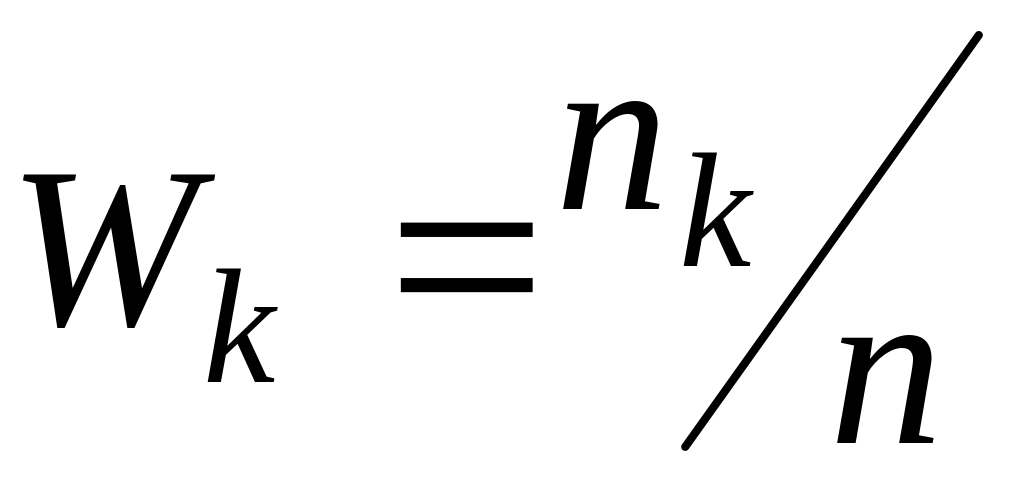 ;
;находятся плотности распределения вероятностей
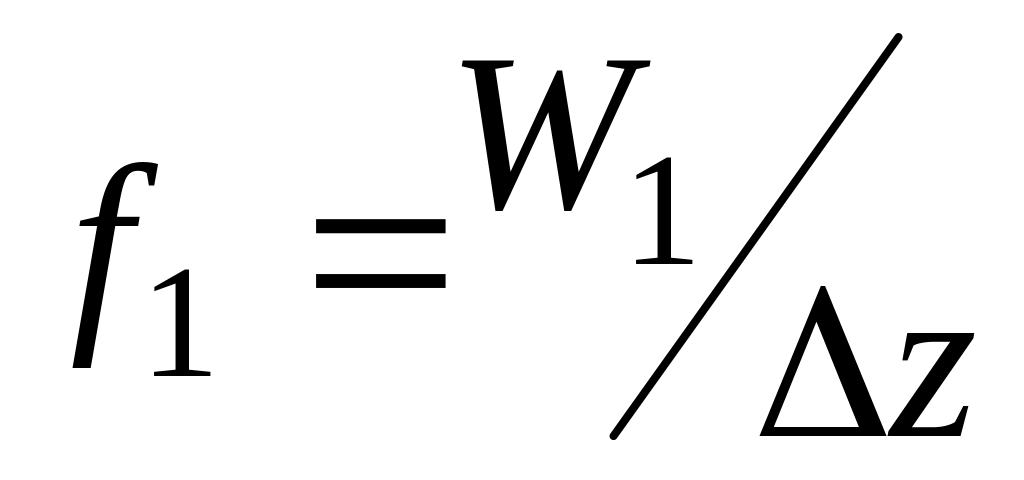 ,
,
 ,…
,…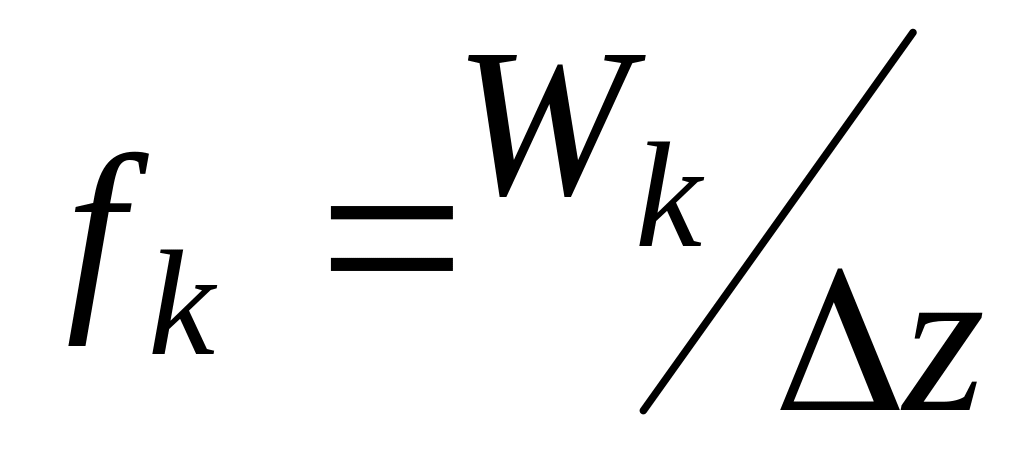 ;
;накопленную вероятность определяют как
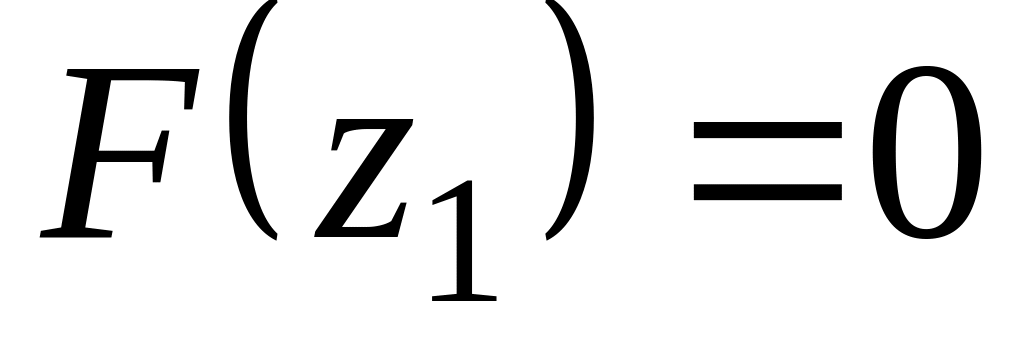 ,
,
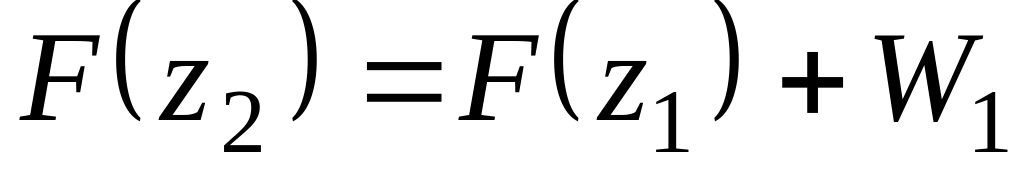 ,…
,…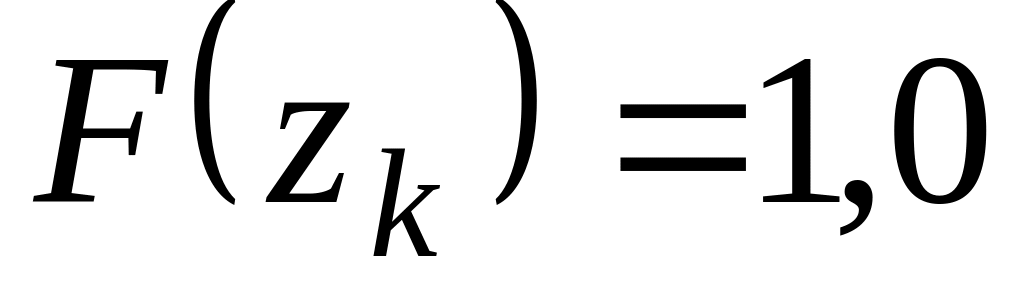 ;
;строят графики функции плотности распределения вероятности и функции распределения вероятности. График функции плотности распределения вероятности, построенный по статистическим данным, называется гистограммой.
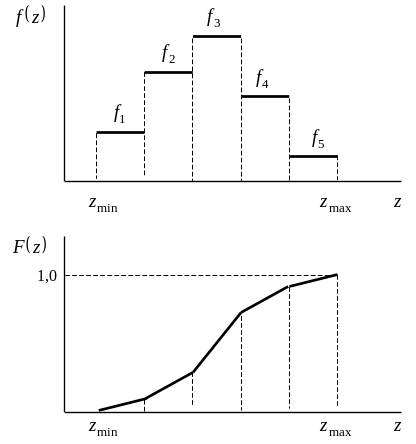
находят характеристики эмпирического распределения – его ассиметрию и вершинность;
подбирают аналитическую зависимость, соответствующую теоретической кривой распределения (закон Вейбулла – Гнеденко, нормальный закон, закон равномерной плотности и т.д.), которая наилучшим образом описывает данное статистическое распределение;
проверяют правильность выбора теоретического закона распределения с использованием критериев согласия. При этом получают ответ на вопрос, являются ли расхождения между статистическим распределением и теоретической кривой случайными, обусловленными малым количеством опытов, или они являются существенными по той причине, что подобранная кривая плохо соответствует данному статистическому распределению.

При использовании критерия Пирсона находят меру расхождения
![]() ,
,
где
![]() - вероятности попадания в разряды,
вычисленные теоретически. При использовании
данного критерия также необходимо
подсчитать число степеней свободы
- вероятности попадания в разряды,
вычисленные теоретически. При использовании
данного критерия также необходимо
подсчитать число степеней свободы
![]() ,
,
где
![]() - число наложенных связей. Примерами
таких условий могут быть
- число наложенных связей. Примерами
таких условий могут быть
![]()
- требование накладывается всегда;
![]()
- совпадение теоретических и статистических средних значений;
![]()
- совпадение
теоретических и статистических дисперсий.
Таким образом, можно принять
![]() .
По мере расхождения и числу степеней
свободы с использованием табличных
данных или аналитически находят
вероятность того, что выбор теоретической
кривой не противоречит опытным данным.
.
По мере расхождения и числу степеней
свободы с использованием табличных
данных или аналитически находят
вероятность того, что выбор теоретической
кривой не противоречит опытным данным.
Если apriori
известен и вид функции
![]() ,
и все входящие в нее параметры (что
случается относительно редко), то можно
использовать критерий
Колмогорова.
При этом определяют величину
,
и все входящие в нее параметры (что
случается относительно редко), то можно
использовать критерий
Колмогорова.
При этом определяют величину
![]() ,
,
где
![]() - максимум модуля разности между
статистической и теоретической функцией
распределения
.
Далее вычисляют вероятность того, что
расхождение между обеими функциями
обусловлено чисто случайными причинами
- максимум модуля разности между
статистической и теоретической функцией
распределения
.
Далее вычисляют вероятность того, что
расхождение между обеими функциями
обусловлено чисто случайными причинами
![]() .
.
По критерию Ястремского вероятность того, что теоретическое распределение не противоречит опытной статистике является существенной, если
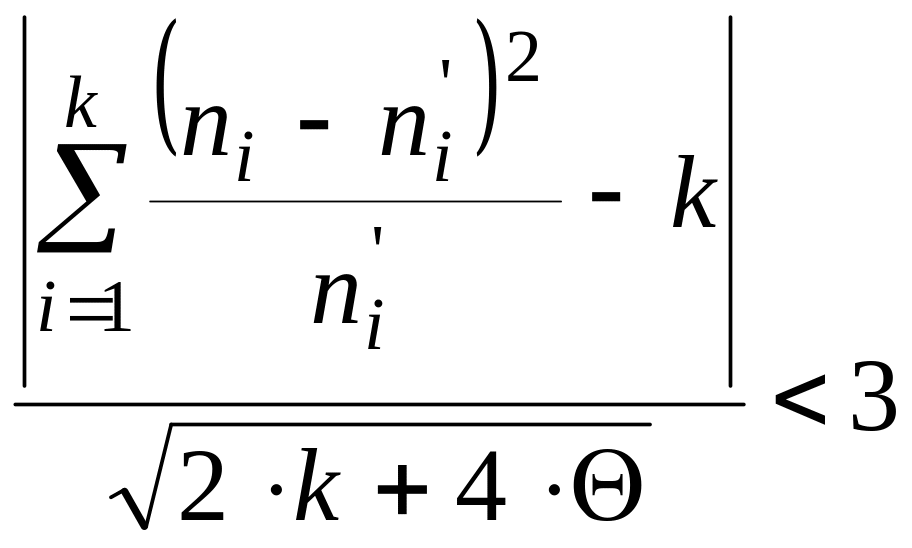 ,
,
где
и
![]() - эмпирическое и теоретическое число
наблюдений в
- эмпирическое и теоретическое число
наблюдений в
![]() разряде. Коэффициент
разряде. Коэффициент
![]() при
при
![]() .
.
