Лаба 1-8 Лабы и ПЗ [Вариант 1] / 5 / ТЧП отчет
.docx1) Цель работы:
1. Изучить алгоритмы цифровой обработки сигналов на основе теоретико-числовых преобразований в конечном поле или кольце целых чисел по модулю чисел Ферма и по модулю чисел Мерсенна.
2. Получение навыков моделирования теоретико-числовых преобразований в среде Matlab.
2) Предварительное задание:
1. а)N=5, ε=2;
M=2q-1, q=5; M=25-1=31;
2 и 31 взаимно простые. Числа 5 и 31 не имеют общих сомножителей.
б) N=7, ε=2;
M=2q-1, q=7; M=27-1=127;
127 и 7 не имеют общих сомножителей. 2 и 127 взаимно простые.
2. Пусть ε=2, M=31, N=5;
n=0:4;
k=0:4;
Q=[1 0 0 0 0; 0 0 0 0 1; 0 0 0 1 0; 0 0 1 0 0; 0 1 0 0 0]
T=mod(2.^(n'*k),31)
T1=Q*T
T =
1 1 1 1 1
1 2 4 8 16
1 4 16 2 8
1 8 2 16 4
1 16 8 4 2
T1 =
1 1 1 1 1
1 16 8 4 2
1 8 2 16 4
1 4 16 2 8
1 2 4 8 16
3. а) ε=2, M=31, N=5;
s=[-1 2 -1 -1 2];
A=mod(s*T,31)
S=mod(A*T1*25,31)
A =1 23 5 5 23
S =30 2 30 30 2
б) ε=2, M=127, N=7;
n=0:6;
k=0:6;
Q=[1 0 0 0 0 0 0; 0 0 0 0 0 0 1; 0 0 0 0 0 1 0; 0 0 0 0 1 0 0; 0 0 0 1 0 0 0; 0 0 1 0 0 0 0; 0 1 0 0 0 0 0];
s=[-2 1 -1 -1 1 1 2];
T=mod(2.^(n'*k),127);
T1=T*Q;
A=mod(s*T,127)
S=mod(A*T1*109,127)
A =1 37 123 4 64 108 30
S =125 1 126 126 1 1 2
3) Лабораторное задание:
1. а)
ТЧП Мерсенна
- Модуль
и длина сигнала
не имеют общих сомножителей.
- Функция Эйлера
Число
является делителем
.
- Сравнение
- Корень
и
являются взаимно простыми.
б)
1.
ТЧП Ферма
где
неотрицательное целое число.
Если
-Модуль
и длина сигнала
не имеют общих сомножителей.
-Функция Эйлера
Число
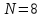является делителем
.
-Сравнение
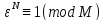
- Корень
и
являются взаимно простыми.
2. а)
n=0:6;
k=0:6;
Q=[1 0 0 0 0 0 0; 0 0 0 0 0 0 1; 0 0 0 0 0 1 0; 0 0 0 0 1 0 0; 0 0 0 1 0 0 0; 0 0 1 0 0 0 0; 0 1 0 0 0 0 0];
s=floor(rand(1,7)*7)
T=mod(2.^(n'*k),127);
T1=T*Q;
A=mod(s*T,127);
a=mod(A.*A,127);
sv1=ifft(fft(s).*fft(s))
sv=mod(109*a*T1,127)
s =3 3 4 0 6 5 5
sv1 =79 94 93 109 102 91 108
sv = 79 94 93 109 102 91 108
б)
1.
n=0:7;
k=0:7;
s=[1 1 0 1 0 1 1 0];
Q=[1 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 1; 0 0 0 0 0 0 1 0; 0 0 0 0 0 1 0 0; 0 0 0 0 1 0 0 0; 0 0 0 1 0 0 0 0; 0 0 1 0 0 0 0 0; 0 1 0 0 0 0 0 0];
T=mod(2.^(n'*k),17);
T1=T*Q;
A=mod(s*T,17);
a=A.*A;
sv1=cconv(s,s,8)
sv=mod(15*a*T1,17)
sv1 =3 4 2 4 3 2 5 2
sv = 3 4 2 4 3 2 5 2
3. а) Ортогональность
n=0:6;
k=0:6;
Q=[1 0 0 0 0 0 0; 0 0 0 0 0 0 1; 0 0 0 0 0 1 0; 0 0 0 0 1 0 0; 0 0 0 1 0 0 0; 0 0 1 0 0 0 0; 0 1 0 0 0 0 0];
T=mod(2.^(n'*k),127);
T1=T*Q;
M=127;
s1 = T(3,:);
s2 = T1(3,:);
s3 = T1(4,:);
p1 = mod(sum(s1.*s2),M)
p2 = mod(sum(s1.*s3),M)
p1 =7
p2 =0
б) Периодичность.
n=0:6;
k=0:6;
T=mod(2.^(n'*k),127);
M=127;
N=7;
s=floor(rand(N,1)*10);
S=mod(T*s,M);
mod(s(5),M)
s(mod((5+N),N))
mod(S(6),M)
S(mod((6+N),N))
ans = 8
ans = 8
ans = 7
ans = 7
в) Симметрия.
n=0:6;
k=0:6;
T=mod(2.^(n'*k),127);
M=127;
N=7;
s=[0 1 2 3 3 2 1];
s*T
ans = 12 210 282 264 264 282 210
г) Симметрия двойного преобразования.
Q=[1 0 0 0 0 0 0; 0 0 0 0 0 0 1; 0 0 0 0 0 1 0; 0 0 0 0 1 0 0; 0 0 0 1 0 0 0; 0 0 1 0 0 0 0; 0 1 0 0 0 0 0];
s=floor(rand(1,7)*7)
T=mod(2.^(n'*k),127);
s1 = mod(T*T*s',M)'
s2= mod(N*Q*s',M)'
s1 = 0 35 42 35 28 21 35
s2 = 0 35 42 35 28 21 35
д) Свойство сдвига.
s1 = [1 2 3 4 5 6 7];
s2 = [4 5 6 7 1 2 3];
A1=mod(T*s1',M)'
A2=mod(T*s2',M)'
e=mod(2.^(4*k),M);
A3=mod(S1.*e',M)'
A1 = 28 7 87 1 119 33 113
A2 = 28 112 47 32 95 80 15
A3 = 28 112 47 32 95 80 15
4. Граф быстрого ТЧП
, N-1=4
Взяв все значения по модулю, получаем Y=[7 13 13 9]
4) Вывод:
В ходе выполнения данной лабораторной работы мы изучили алгоритмы цифровой обработки сигналов на основе теоретико-числовых преобразований в конечном поле или кольце целых чисел по модулю чисел Ферма и по модулю чисел Мерсенна. Так как ТЧПФ имеет длины преобразований, которые выражаются составными числами, то это позволяет для их вычисления использовать алгоритмы типа БПФ. Основное применение ТЧП – это вычисление точных значений свертки.