1.5. Выполните свертки

Пусть даны две апериодические последовательности {S(n)} и {h(n)} одинаковой длины N. Линейная свертка этих последовательностей имеет длину 2N – 1. Каждая из последовательностей дополняется нулями до длины 2N – 1. Линейную свертку выполня­ем на основе свойства (теоремы) циклической свертки с помощью ТЧП. Для этого не­обходимо выполнять следующие последовательности операций:

I. Вычисление ТЧП последовательности {S(n)}:

, ,

где

2. Вычисление ТЧП последовательности {h(n)}:

,

где .

3 . Перемножение полученных ТЧП:

,

4. Находим обратное ТЧП последовательности:

, ,

где, а величина определяется из решения сравнения .

2.6. Быстрое вычисление свертки с помощью теоретико-числового преобразования Ферма

Для вычисления может быть использован алгоритм быстрого ТЧПФ, подученный как разложение по основанию 2 на ступени (итерации) с постоянной структурой путем прореживания по частоте или прореживания по времени. Основным вычислительный для алгоритма быстрого ТЧПФ по основанию 2 является устройство выполнения базовой операции "бабочка". Структура быстрого поточного ТЧПФ процессора идентична структуре поточного БПФ процессора, за исключением блока выполне­ния операции "бабочка", в котором вместо умножения на (в случае БПФ) осуществляется умножение на 2^k. На рис .1 показана базовая операция "бабочка" для

алгоритма быстрого ТЧПФ с прореживанием по времени.

Рис. 1

На рис. 2 изображен направленный граф четырехтомного алгоритма ТЧПФ с прореживанием по частоте.

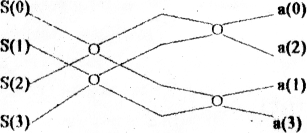
Рис.2

0. Теоретико-числовое преобразование Мерсенна

Пусть q — простое число, положим . Числа Мерсенна являются простыми при q = 2, 3, 5, 7, 13, 17, 19, 31, 61 .

Преобразование Мерсенна q точной последовательности определяются следую­щим образом:

,

Обратное преобразование Мерсенна определяется как

,

При этом ((q*q – 1)) = 1, все показатели степени берутся по модулю q и все опера­ции пополняются по модулю P.

Основным преимуществом преобразования является возможность выполнения умножения по степени 2 просто как поразрядных циклических сдвигов.

3 . ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ

Программа работает в диалоговом режиме как система открывающихся окон. В каждом разделе существует разветвленная система подсказок, что позволяет упростить работу с ней.

Лабораторная работа на основе данной программы состоит из двух основных частей: вычисление прямого и обратного ТЧП, вычисление свертки и корреляционной функции.

После прохождения заставки, прерывающейся при нажатии любой из клавиш, появляется славное меню, выбор пунктов в котором осуществляется клавишами вверх и вниз я нажатием клавиши "ввод". Меню состоит из четырех пунктов: введение, вы­числение прямого и обратного ТЧП, вычисление свертки и корреляционной функции и выхода из программы в среду ДОС.

Во введении даются основные теоретические сведения о ТЧП и описание работы с программой.

Второй пункт меню является первой частью лабораторной работы. При его выборе появляется окно, в котором необходимо выбрать параметры теоретико-числового преобразования. Один или два параметра могут быть заданы преподавателем, остальные студент должен ввести самостоятельно, используя материал, данный во введении, и в "помощи" они появляются при нажатии соответствующей клавиши.

При правильно введенных параметрах ТЧП появится запрос на введение элементов входной последовательности. После введения и корректировки этих элементов, необходимо будет построить матрицу преобразования. Затем будет вычислено прямое ТЧП. Далее студент должен будет преобразовать матрицу для обратного ТЧП, после чего будет вычислено обратное теоретико-числовое преобразование. На этом данный раздел программы будет закончен.

Третий пункт меню является второй частью лабораторной работы. Так же, как и при выборе второго пункта меню, появляется окно, в котором необходимо выбрать параметры ТЧП. После их ввода, необходимо будет ввести две входные последова­тельности. После этого студент должен вычислить свертку или корреляционную функ­цию, фиксируя на каждом шаге результаты и делая выводы (вычисления прямого ТЧП заданных последовательностей, перемножение сигналов и вычисления обратного ТЧП ПЭВМ будет производить сама).

4. ПРЕДВАРИТЕЛЬНОЕ ЗАДАНИЕ

4.1. Задаваясь числом отсчетом N = {5,7} и основанием а = 2, определить модуль, с которым будет выполняться прямое и обратное теоретико-числовые преобразования.

4.2. Построить прямую и обратную матрицу ТЧП для заданных параметров.

4.3. Вычислить прямое и обратное ТЧП для последовательностей : S(n) = {-1,1,-1, -1,1} (при N = 5), S(n) = {-1,1,-1,-1,1,1,1} (при N = 7).

4.4. Найти четырехточечную циклическую свертку последовательности (1, 2, 0, 0) саму с собой с помощью графа быстрого ТЧН.

5. ЛАБОРАТОРНОЕ ЗАДАНИЕ

5.1. Получить у преподавателя два из трех параметров ТЧП (N, М, а). Опреде­лить один из оставшихся параметров.

5.2. Построить матрицу прямого ТЧП.

5.3. Задаться входной цифровой последовательностью и с помощью программы вычислить прямое ТЧП.

5.4. Построить матрицу обратного ТЧП.

5.5. Вычислить обратное ТЧП и сравнить результат с входной последовательностью. Сделать вывод.

56. Дня заданной преподавателем входной последовательности определить па­раметры ТЧП, выполнить быстрое ТЧП, построить графы быстрого ТЧП. Оценить вычислительную сложность алгоритма.

5.7. С помощью программы вычислить автосвертку, фиксируя все промежуточ­ные результаты и производя необходимые зарисовки графов, графиков свертки.

5.8. С помощью программы вычислить автокорреляционную функцию, фиксируя все промежуточные результаты и производя зарисовки графиков. Сделать выводы.

5.9. Построить структурную схему процессора ТЧП, вычисляющего свертку (корреляционную функцию).

6. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ

6.1. Показать, что правила умножения и сложения в поле Галуа (GFP^k) удовлетворяют аксиомах: кольца (р — простое число , k — целое положительное число).

6.2. Вычислить 9²/3, М = 64.

6.3. Найти решение в кольце целых чисел 8²/4 для М = 64.

64. При каких условиях возможно выполнение ТЧП в кольце целых чисел?

6.5. Какие системы базисных функций используются в ТЧП?

6.6. Перечислите и поясните основные свойства ТЧП.

6.7. Поясните, из каких соображений выбираются параметры ТЧП.

6.8. Вычислите спектр последовательности (1, 1, -1, -1) на основе ТЧП Мерсенна.

6.9. В чем заключаются преимущества и недостатки ТЧП в сравнении с ДПФ?

6.10. Построить графы быстрого ТЧП (N = 4, N = 8, n = 16).

6.11. Как использовать матрицы прямого ТЧП для вычисления обратного ТЧН?

6.12. Вычислите обратное ТЧП для спектра, найденною в п. 6.8.

6.13. Вычислите свертку последовательности (1, 1, 1, -1) прямым методом с по­мощью ТЧП.

6.14. Вычислите корреляционную функцию последовательности (1, 1, 1,-1 ) прямым методом и с помощью ТЧП.

6.15. Составьте вычислительную ДПФ, БПФ, ТЧП.

6.16. Можно ли вычислить линейную свертку с помощью циклической свертки?

6.17. Вычислить числа, обратные числам 5, 7, 8 ( М = 31), (М = 23, L = 9), используя теорему Эйлера.

6.18. Найти обратный элемент (М = 31, L = 7), с применением алгоритма Евклида.

6.19. Объясните, что такое псевдоперевыполнение и когда оно возникает.

6.20. Поясните, при использовании, каких чисел в качестве модуля возможны быстрые алгоритмы вычисления ТЧП и почему.

Литература

1. Лосев В.В. Микропроцессорные устройства обработки информации. Алгоритмы цифровой обработки. - Мн.: Высш. шк., 1990.

2. Крот А.М., Минервина Е.Б. Быстрые алгоритмы и программы цифровой спектральной обработки сигналов и изображений. - Мн.: Навука i тэхнiка, 1995.

3. Макклеллан Дж., Рейдер Ч.М. Применение теории чисел в цифровой обработ­ке сигналов. - М.: Радио и связь, 1983.

4. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. - М.: Мир 1989.

5. Залманзон Л.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях. - М.: Науки, 1989.

Св. план 1997, поз. 95

Учебное издание

ТЕОРЕТИКО-ЧИСЛОВЫЕ ПРЕОБРАЗОВАНИЯ

Методические указания к лабораторной работе по курсам

"Прикладная теория кодирования",

"Цифровая обработка сигналов",

"Зашита информации"

душ студентов радиотехнических специальностей

Составитель Митюкин Анатолий Иванович

Редактор Т.М. Лейко

Корректор Е.Н. Багурчик

Подписано в печать 14.06.97. Формат 60 х 84 1/16

Объем 1,16 усл. печ. 1,0 уч. изд.л. Тираж 200 экз.

Заказ 340.

Белорусский государственный университет информатики и радиоэлектроники Министерства образования Республики Беларусь

Отпечатано на ротапринте БГУИР. 220027, Минск, И.Бровки.6.

19