3. Численное решение обыкновенных дифференциальных уравнений

3.1 Численное решение дифференциальных уравнений методами Эйлера, модифицированным методом Эйлера, Рунге-Кутты

Пусть на отрезке [a,b] требуется найти функцию y=y(x) , удовлетворяющую уравнению y’=f (x,y) и начальному условию .

Здесь f(x,y) - заданная непрерывная функция заданных аргументов. Решить приведенную задачу численно – это значит для заданной последовательности чисел , ,…, из отрезка [a,b] и числа , не находя самого решения y=y(x) , вычислить (приближенно) значения , ,…, этого решения в точках , ,…, .

В этом случае можно искомую интегральную функцию y=y(x) заменить ломаной, вершинами которой являются точки , ; при условии, что направление отрезка [ , ] совпадает с направлением интегральной кривой в точке . Иначе говоря, необходимо, чтобы

, , , (3.1.1)

Из (3.1.1) следует:

(3.1.2)

Формула (3.1.2), которую называют формулой Эйлера, позволяет вычислить значения , т.е построить ломаную, аппроксимирующую искомую интегральную кривую. Нетрудно показать, что погрешность формулы (3.1.1) равна .

Метод Рунге-Кутты

Метод Рунге-Кутты характеризуется повышенной точностью и принадлежит к многошаговым методам численного интегрирования задачи Коши: Пусть h – шаг интегрирования. Вычисление приближенного значения при решении задачи Коши в точке методом Рунге-Кутты заключается в выполнении операций, связанных с определением на каждом k-ом шаге коэффициентов

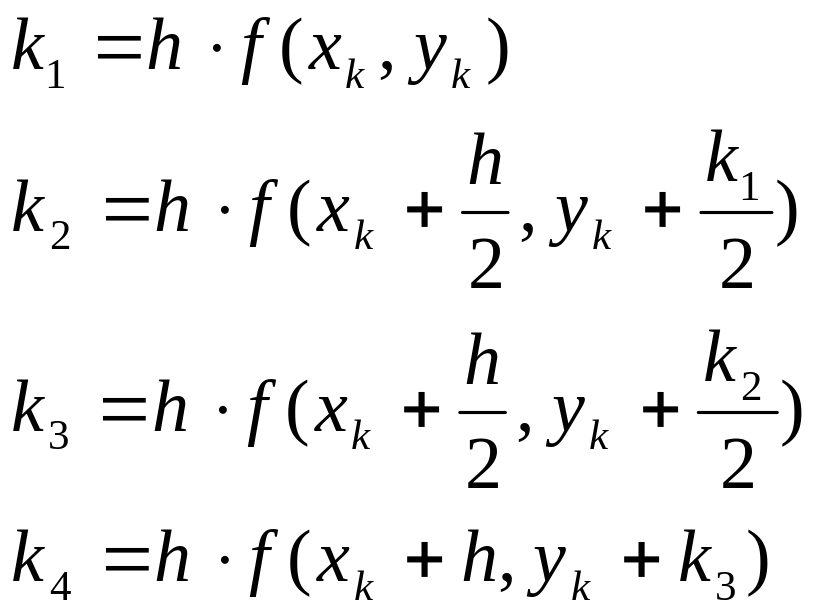
и далее значений

3.2 Решение заданного дифференциального уравнения методами Эйлера и модифицированным методом Эйлера

Решение было получено с помощью программы на языке Си. Текст программы приведён в приложении A.

Результаты вычислений:

Рисунок 3.1— Значения функции, вычисленные методом Эйлера

На рисунке 3.1 y_i — значения функции , x₁ — начальное значение аргумента, h — приращение аргумента

Рисунок 3.2— Значения функции, вычисленные модифицированным методом Эйлера

На рисунке 3.2 y_i — значения функции , x₁ — начальное значение аргумента, h — приращение аргумента

3.3 Решение заданного дифференциального уравнения методом

Рунге-Кутты

Решение было получено с помощью программы на языке Си. Текст программы приведён в приложении A.

Результаты вычислений:

Рисунок 3.3 — Вычисление значений функции методом Рунге-Кутты

На рисунке 3.2 y_i — значения функции , x₁ — начальное значение аргумента, h — приращение аргумента

Метод Рунге-Кутты является наиболее точным методом решения, т.к. его погрешность на порядок меньше погрешности, даваемой методом Эйлера. Также он обладает следующими достоинствами:

• этот метод является одноступенчатым и одношаговым;

• требует информацию только об одной точке;

• имеет небольшую погрешность;

• значение функции рассчитывается при каждом шаге.