Векторный и координатный метод решения задач геометрии

1.Декартовы координаты и векторы в пространстве

Векторы в пространстве

Определение 1

Величины, которые характеризуются численным значением и направлением называются векторными ( или векторами) .

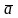Векторы задаются направленными отрезками, т.е. отрезками, у которых указано начало (точкой ) и конец (стрелкой) рис. 96. Обозначение , читается “вектор AB” или , читается “вектор a”. Один и тот же вектор может изображаться бесконечным числом направленных отрезков.

Определение 2

Модуль вектора – это длина отрезка AB, обозначается |AB|, модуль вектора называется так же длиной вектора.

Определение 3

Сонаправленными называются векторы, если они лежат на параллельных прямых в одной полуплоскости относительно прямой , соединяющей их начала).

Определение 4

Противоположно направленными называются векторы, если они лежат на параллельных прямых в разных полуплоскостях относительно прямой, соединяющих их начала.

Определение 5

Векторы называются равными, если их длины равны и они сонаправлены.

На рис.99 векторы AB = CD =NM.

Определение 6

Вектор называется нулевым, если его начало и конец совпадают: вектор

нулевой.

Определение 7

Противоположными векторами называют два вектора, если они противоположно направлены и длины их равны. Обозначают: a и –a .

Определение 8

Коллинеарными векторами называются векторы сонаправленные или противоположно направленные. Векторы a,b,c,d коллинеарные.

Определение 9

Компланарными векторами называются векторы, параллельные некоторой плоскости Векторы a,b,c,d компланарны.

Отложить от данной точки вектор, равный данному, - значит построить направленный отрезок с началом в данной точке, изображающий данный вектор.

Действия с векторами и их свойства=2

1.Сумма векторов (правило треугольника)

Чтобы найти сумму векторов a и b, надо:

1.Отложить от какой – либо точки A вектор AB равный вектору a;

2.От точки B отложить вектор BC, равный b;

3.Вектор AC будет суммой векторов a и b.

Неравенство треугольника |AB|+|BC| |AC|

2. Сумма векторов (правило параллелограмма)

Чтобы найти сумму векторов a и b, надо:

1.Отложить от какой – либо точки a вектор ab равный вектору a

2.Отложить от этой же точки вектор AD, равный b.

3.Построить на векторах AB и AD как на сторонах параллелограмм ABCD;

4. Суммой векторов a и b, будет вектор AC – диагональ параллелограмма.

3. Разность векторов.

Чтобы найти разность векторов a и b, надо:

1 Отложить от какой – либо точки a вектор ab равный вектору a .

2.Отложить от этой же точки вектор AC, равный b.

3. Разностью векторов a и b будет вектор CB.

=

4. Умножение вектора на число.

Чтобы умножить вектор a на число k 0, надо:

1.Найти длину вектора – произведения , она равна длине вектора a, умноженной на модуль числа k: |k||a|;

2.Определить направление вектора – произведения: если k > 0, то он сонаправлен с вектором a; если k < 0, то он противоположно направлен с вектором a.

5.Свойства сложения векторов

1.Переместительный закон: a + b = b + a;

2. Сочетательный закон (a + b)+ c = a +(b+c);

3.a +( -a) =0;

4. a + 0 =a.