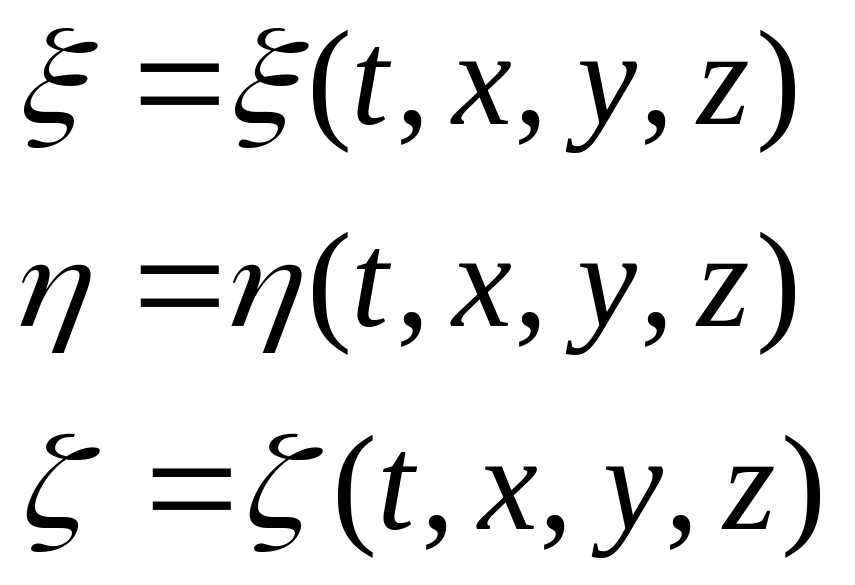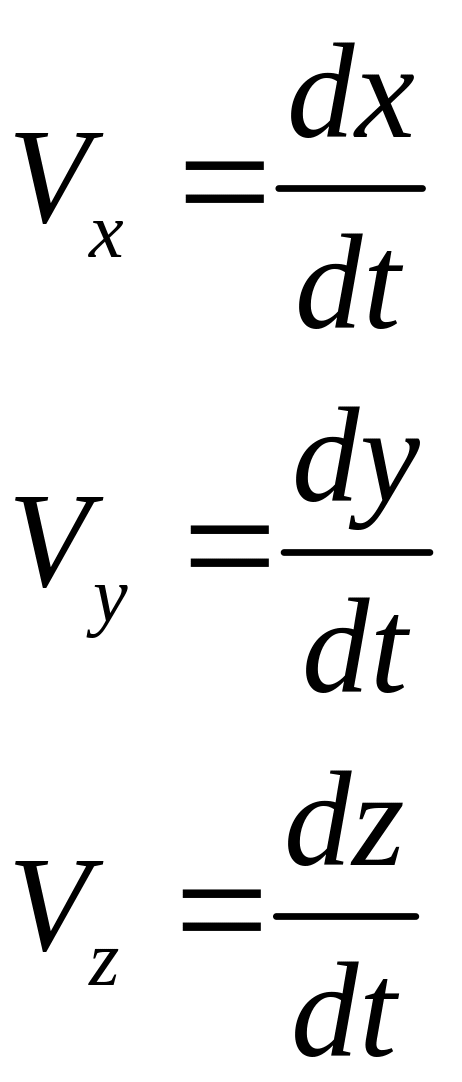- •Механика сплошных сред. Точечно-векторное аффинное пространство.
- •Векторное произведение.
- •Инварианты тензора второго ранга.
- •Тензор дивиатр и шаровой (сферический тензор).
- •Собственные значения и собственные вектора.
- •Разложение тензора по собственному базису.
- •Симметричные тензоры.
- •Тензорная поверхность.
- •Струя. Поверхность тока. Трубка тока.
- •Движение элементарного объёма как абсолютно твёрдого тела.
- •Аффинная деформация элементарного объёма.
- •Тензор поворота.
- •Компоненты вектора перемещения и компоненты тензора деформации.
- •Первая теорема Гейнгольца а перемещениях.
- •Совместность деформаций Коши.
- •Инвариант тензора деформации.
- •Задача о кручении стержня.
- •Кинематика микрополярной среды Коссера.
- •Кинематика микроморфной среды.
- •Истинные деформации.
- •Тензор скоростей деформации.
- •Кинематический смысл компонент тензора скоростей деформации.
- •Инварианты тензора скоростей деформации.
Собственные значения и собственные вектора.
Собственными значениями
![]() и соответствующими собственными
векторамми
и соответствующими собственными
векторамми
![]() и
и
![]() и тензора второго ранга
называют
числа и тройки векторов, удовлетворяющих
следующим значениям.
и тензора второго ранга
называют
числа и тройки векторов, удовлетворяющих
следующим значениям.
![]()
![]()
![]()
![]() запишем в индексном виде
запишем в индексном виде
![]()
![]()
![]()
Потребуем чтобы
![]() и
и
![]()
Тогда система имеет нетривиальное
решение:
![]()
Заключение:
![]()
![]()
Теорема Собственные вектора являются ортогональными векторами.
Доказательство:
![]()
![]() вычтем выражения, получим
вычтем выражения, получим
![]() вектора
ортогональны
вектора
ортогональны
![]()
Разложение тензора по собственному базису.
,
где
![]() и
и
![]() базисные
вектора некоторой системы координат.
базисные
вектора некоторой системы координат.
![]()
![]()
![]()
![]()
![]()
Все недиагональные вектора равны нулю.
Надо найти векторные значения.
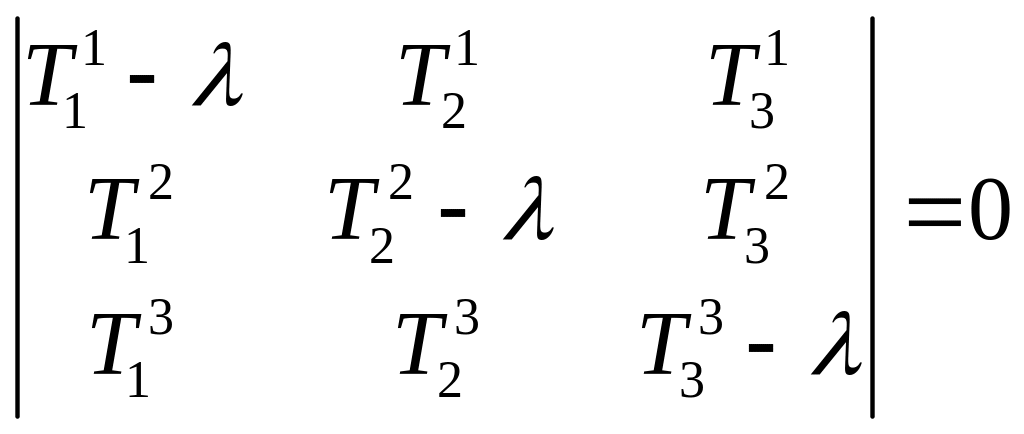
![]()
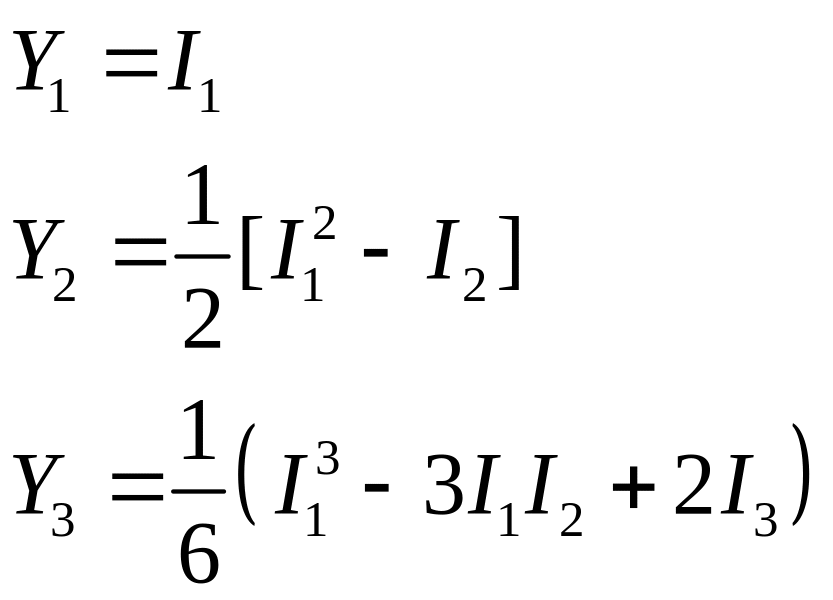
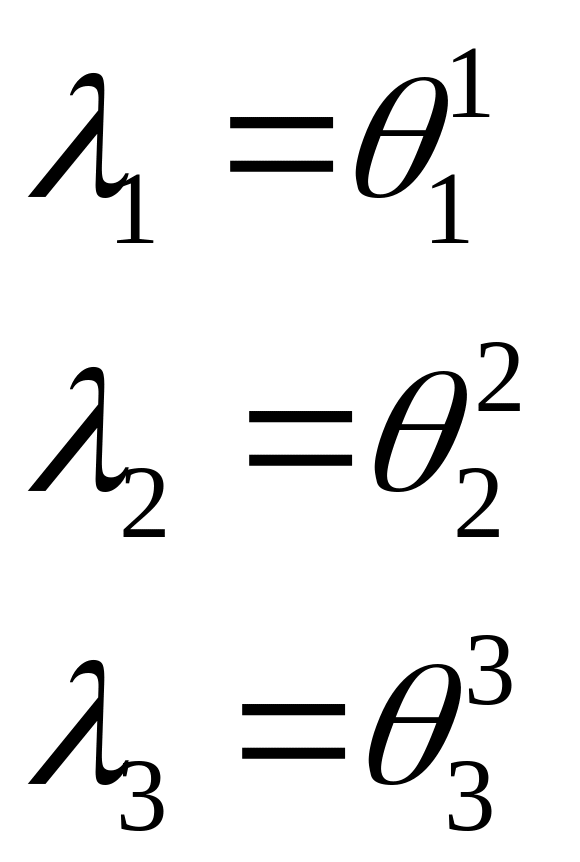 суммирование по j, а i
и k фиксированные индексы.
суммирование по j, а i
и k фиксированные индексы.
Симметричные тензоры.
![]()
![]() Два тензора второго ранга называются
коаксиальными, если их собственные
базисы совпадают, т.е. если один имеет
диагональный вид, то и другой должен
иметь диагональный вид. Положительно
определённым тензором второго ранга
является тензор, для которого выполняется
соотношение
Два тензора второго ранга называются
коаксиальными, если их собственные
базисы совпадают, т.е. если один имеет
диагональный вид, то и другой должен
иметь диагональный вид. Положительно
определённым тензором второго ранга
является тензор, для которого выполняется
соотношение
![]() ,
ненулевой
вектор.
,
ненулевой
вектор.
Теор.1 Собственные значения симметричного тензора второго ранга всегда вещественные.
Теор.2 Собственные значения симметричного положительно определённого тензора всегда положительны.
Тензорная поверхность.
Каждому симметричному тензору второго ранга можно поставить в соответствие некоторую поверхность, называемую тензорной поверхностью в соответствии со следоющими правилами:
![]()
![]() и
и
![]() некоторые координаты.
некоторые координаты.
![]()
![]()
![]()
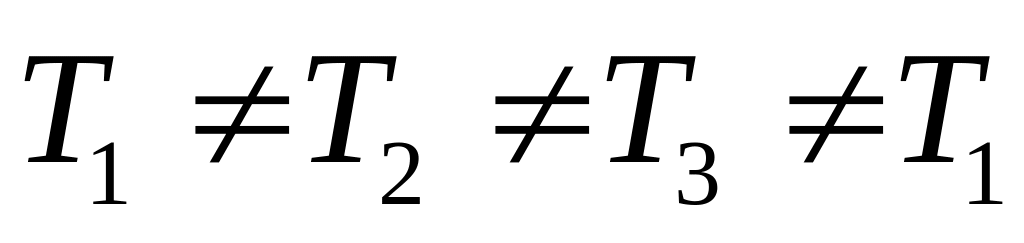
 существует и единственна система
координат, в которой она имеет диагональный
вид.
существует и единственна система
координат, в которой она имеет диагональный
вид.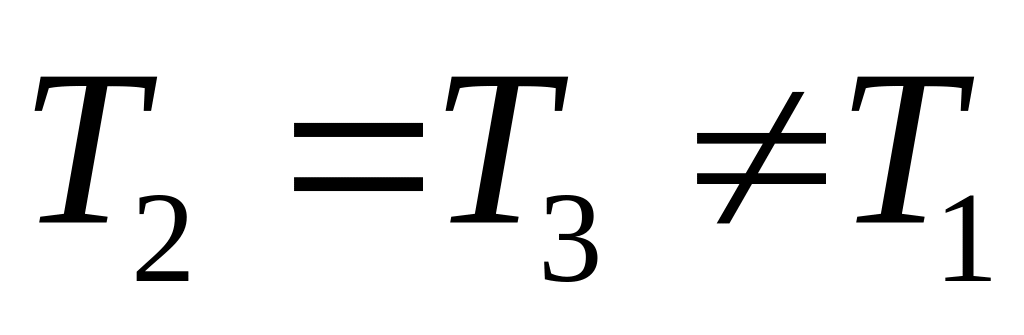
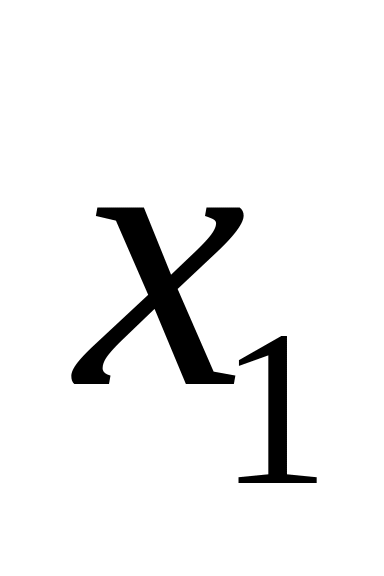 и
и
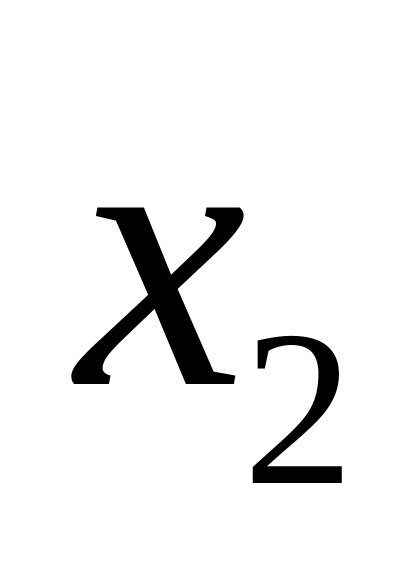 выбраны принципиально, а
выбраны принципиально, а
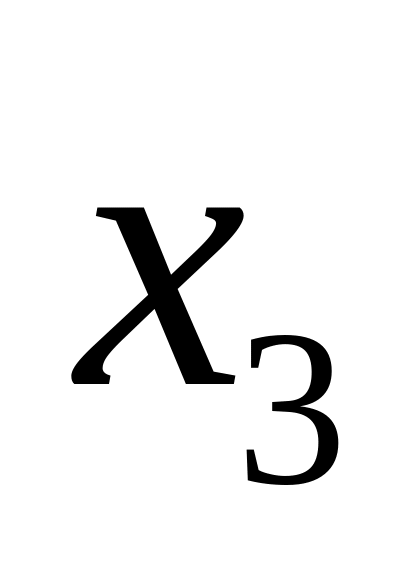 произвольно.
произвольно.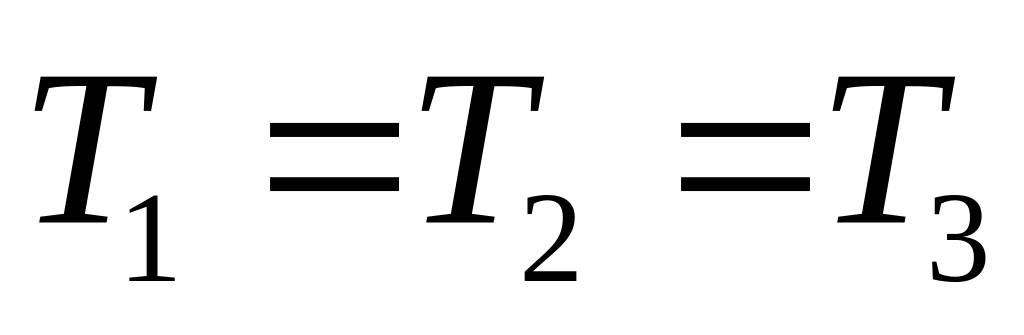 направление осей можно задавать
произвольно.
направление осей можно задавать
произвольно.
Физические компоненты вектора и тензора.
Ортогональный и иртонормированный базис.
![]()
![]()
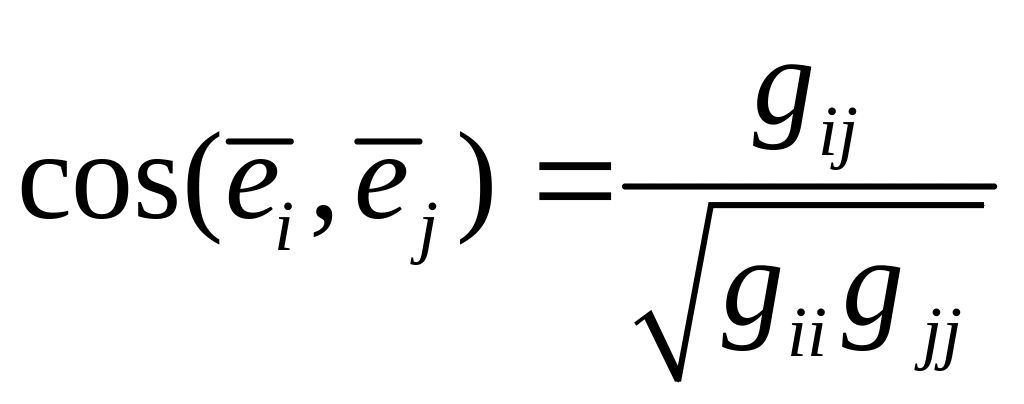
![]()
![]()
![]()
![]()
Введём нормированный базис.
![]()
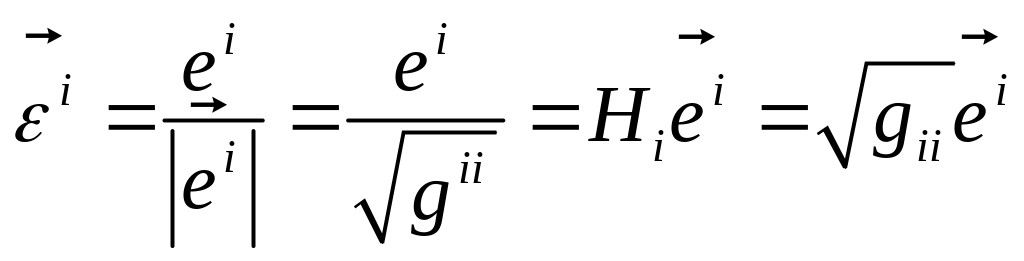
Покажем, что в ортонормированном базисе вектора основного и взаимного базиса совпадают.
![]()
![]()
![]()
Хотим показать, что
![]()
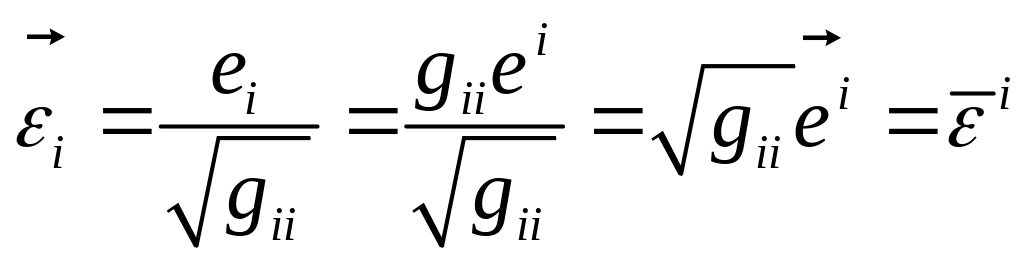
Компоненты вектора и тензора в ортонормированном базисе.
![]()
![]()
![]() - физические компоненты вектора.
- физические компоненты вектора.
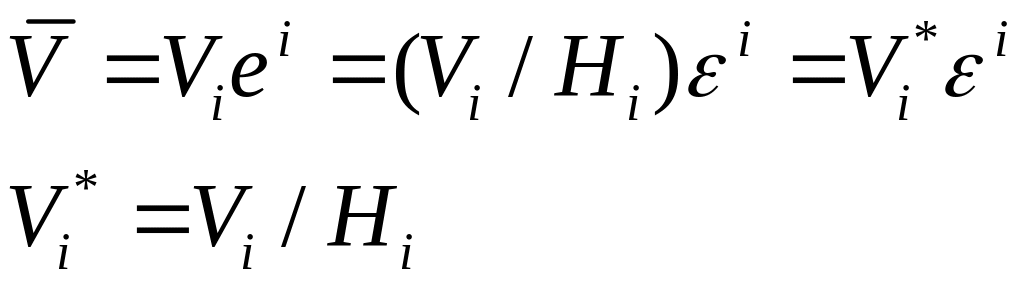
![]() - физические компоненты не зависят от
того с каким базисом мы имеем дело.
- физические компоненты не зависят от
того с каким базисом мы имеем дело.
![]()
![]()
![]()
Векторный и тензорный анализ.
Скалярное поле.
Пусть в каждой точке пространства задана
![]()
![]() ,
говорят что в этом случае определено
скалярное поле.
,
говорят что в этом случае определено
скалярное поле.
![]() - приращение функции вдоль координатной
поверхности.
- приращение функции вдоль координатной
поверхности.
Разделим это выражение на
![]() .
.
![]() координатная производная или ковариантная
производная .
координатная производная или ковариантная
производная .
![]()
![]()
![]()
Градиент скаляра.
Введём в рассмотрение вектор, направленный по нормали к поверхности постоянных значений функций, в сторону её возростания и имеющий величину, равную произведению функции на скаляр, назовём этот вектор градиентом скаляра.
![]() ковариантная производная.
ковариантная производная.
![]()
![]() контравариантная производная
контравариантная производная
![]()
![]()
![]()
Векторное поле.
Пусть в каждой точке пространства задана
некоторая функция
![]()
![]() ,
говорят, что в этом случае задано
векторное поле.
,
говорят, что в этом случае задано
векторное поле.
Символы Кристоффеля второго рода.
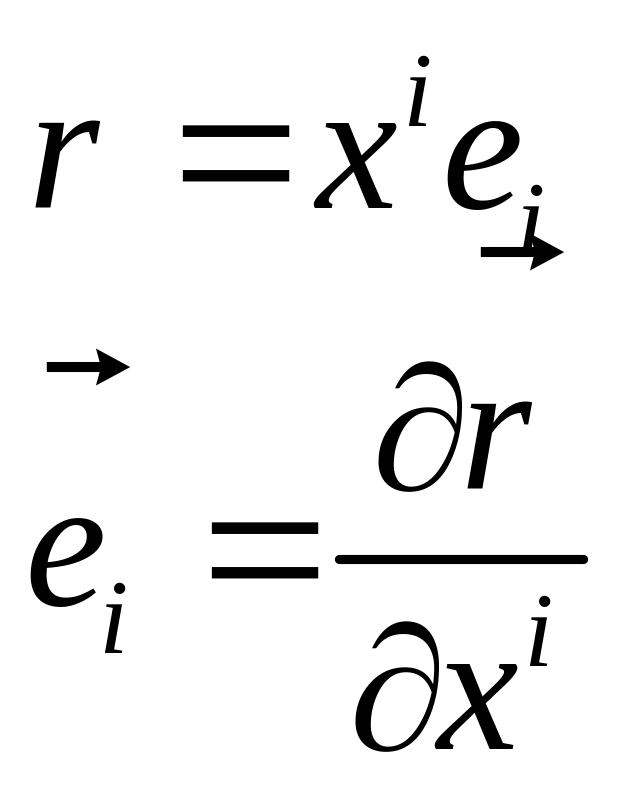
![]()
![]() - символы Кристоффеля второго рода.
- символы Кристоффеля второго рода.
Свойства:
Символы Кристоффеля не являются компонентами тензора третьего ранга.
Символы Кристоффеля второго рода являются симметричными по нижним индексам.
![]()
Определим производную по координатам от векторов взаимного базиса. Пойдём в обход.
![]()
![]()
![]()
Установим связь символов Кристоффеля с компонентами метрического тензора.
![]()
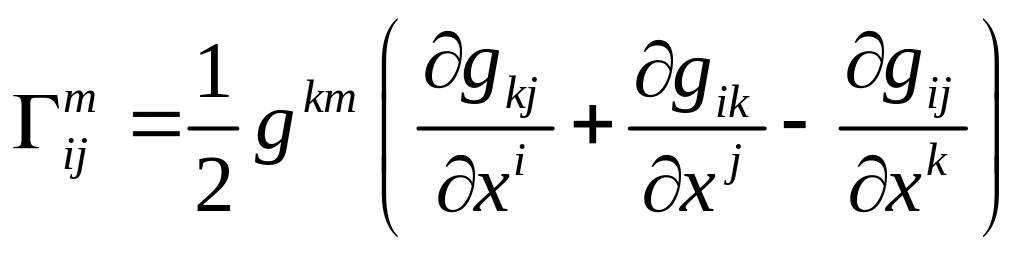
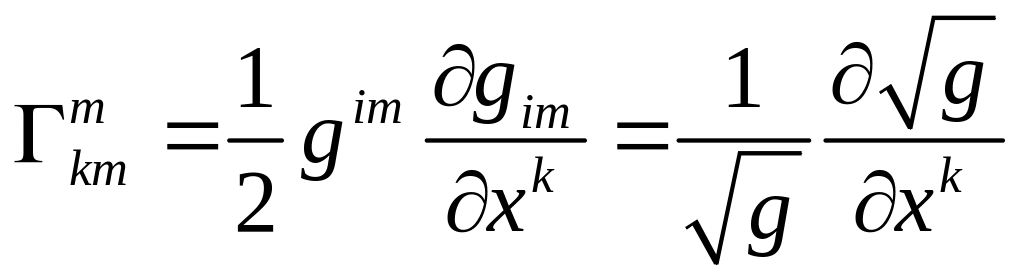
Введём в рассмотрение символы Кристоффеля первого рода:
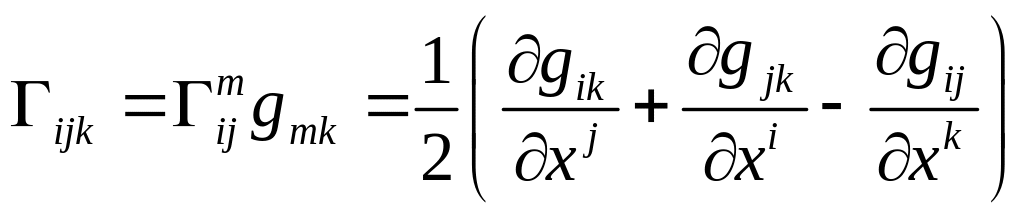
Дифференцирование вектора по координатам.
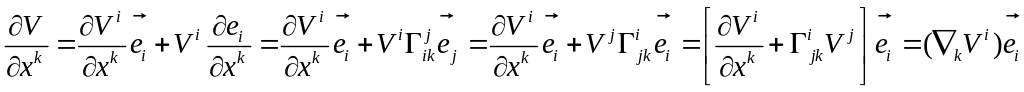
Ковариантная производная от контрвариантных компонент вектора.
![]()
Ковариантная производная от ковариантных компонент вектора.
![]() контравариантная производная от
ковариантных компонент вектора.
контравариантная производная от
ковариантных компонент вектора.
![]() контравариантная производная от
контрвариантных компонент вектора.
контравариантная производная от
контрвариантных компонент вектора.
Набла оператор.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дивергенция вектора.
![]()
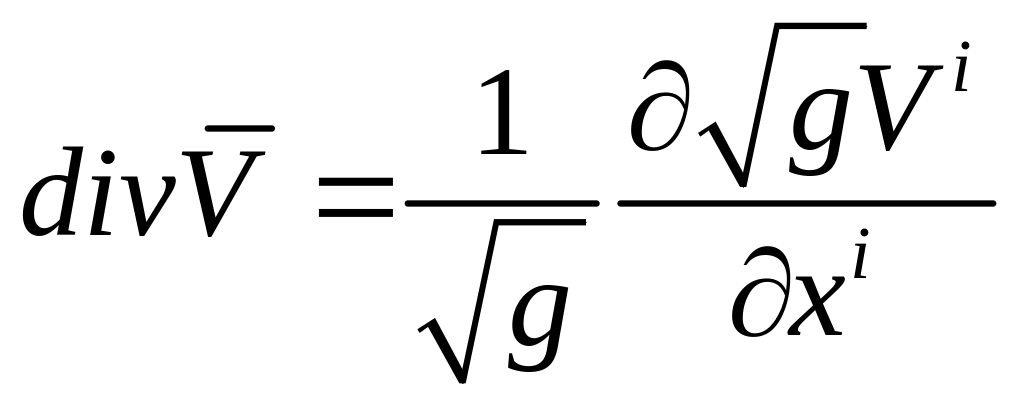
![]()
![]() - вектор вихря
- вектор вихря
![]() - тензор вихря.
- тензор вихря.
![]() - тензор второго ранга.
- тензор второго ранга.
![]() - дивергенция вектора.
- дивергенция вектора.
Левая деформация:
![]()
Правая деформация:
![]()
Тензорное поле.
Пусть в каждой точке пространства задано
![]()
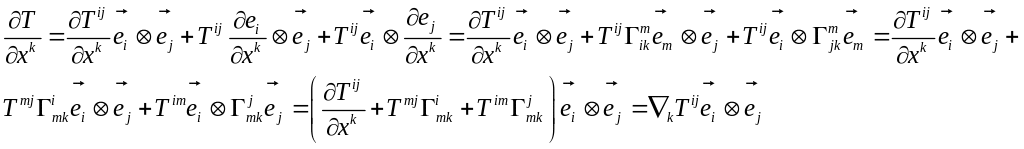
Ковариантная производная от ковариантной производной вектора.
Ковариантная производная от ковариантной компоненты.
![]()
![]()
Ковариантная производная от смешанных компонент.
![]()
![]()
Ковариантная производная метрической матрицы. Теорема Риччи.
Теор. Риччи: Ковариантная производная метрической матрицы и её определитель равны нулю.
Д-во:
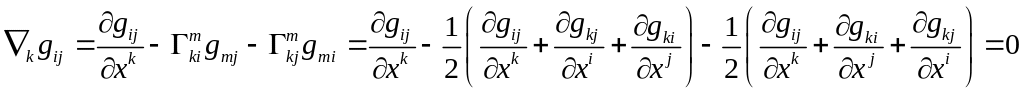 т.е.
т.е.
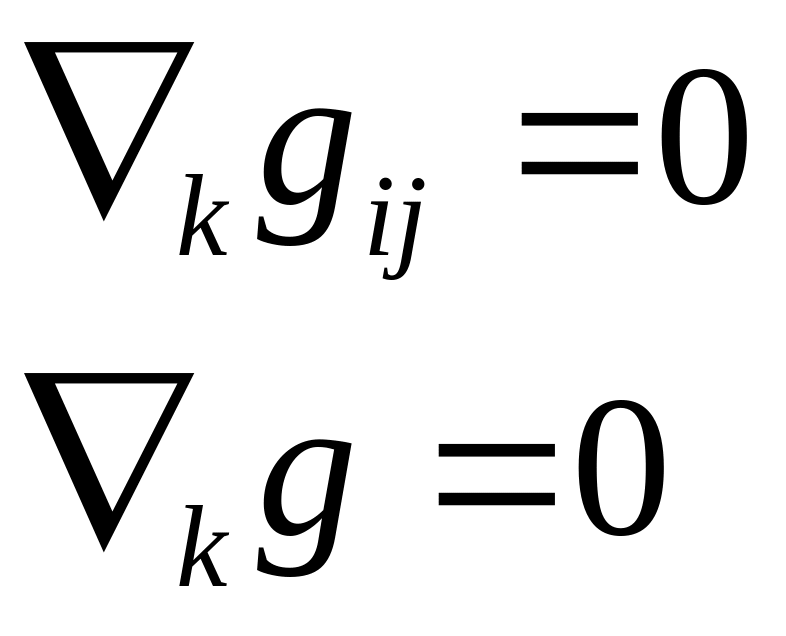
Дивергенция тензора.
![]()
![]()
![]()
Ковариантная производная второго порядка.
![]()
![]() - Лапласиан.
- Лапласиан.
![]() - Лапласиан вектора.
- Лапласиан вектора.
![]() - Лапласиан тензора.
- Лапласиан тензора.
Оператор несовместности
![]()
Дифференцирование в ортогональных криволинейных координатах.
![]()
Символы Кристоффеля второго рода в ортогональных координатах.
![]()
![]()
![]()
![]()
![]()
![]()
Производные от векторов ортонормированного базиса.
![]()
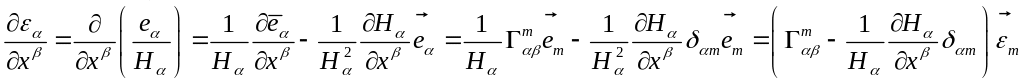
![]()
![]()
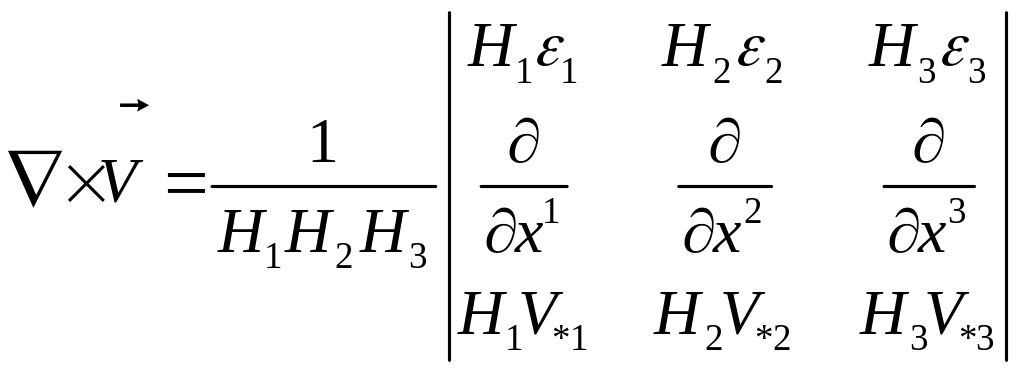
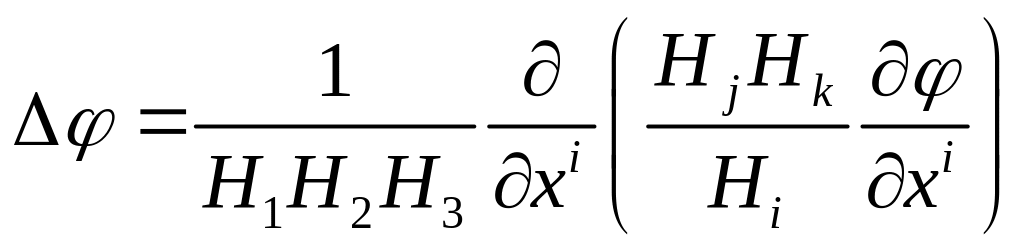
![]()
![]()
Суммируем по i, а i и k делаются так, что они не совпадают друг с другом.
Интегрирование векторных и тензорных величин.
![]()
![]()
![]()
Криволинейные интегралы. Криволинейные интегралы первого рода.
Пусть задана
![]()
![]()
![]()
тогда можно составить интегральную сумму.
![]()
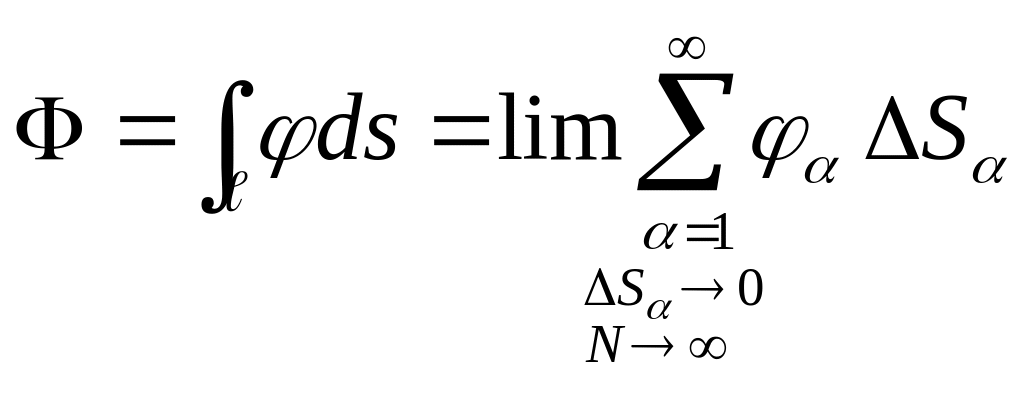
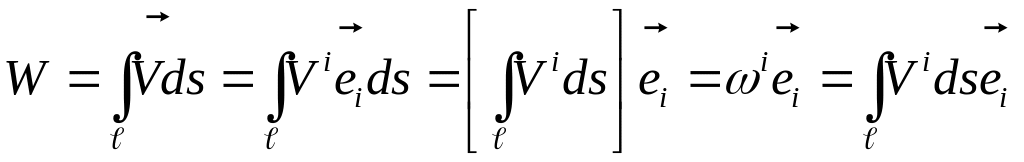
![]()
Криволинейный интеграл второго рода.
![]()
![]()
![]()
![]() осуществляем предельный переход
осуществляем предельный переход
![]() - скалярный криволинейный интеграл
второго рода.
- скалярный криволинейный интеграл
второго рода.
Второй криволинейный интеграл второго рода.
![]()
Тензорный криволинейный интеграл второго рода.
![]()
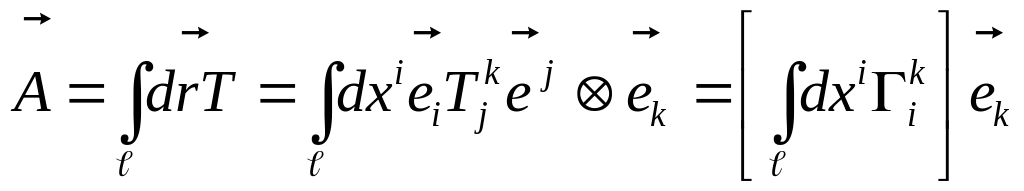
![]()
![]()
Потенциальный вектор и тензорное поле.
![]()
Говорят что векторное поле
-
потенциально, если существует
![]() что выполняется соотношение
что выполняется соотношение
![]()
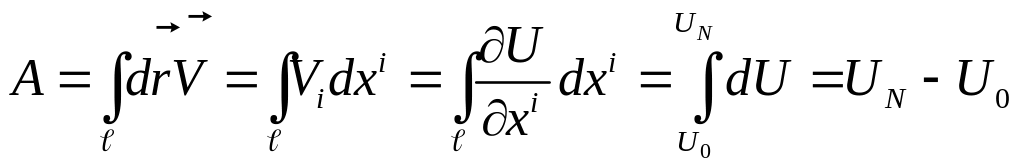
Говорят, что тензорное поле
![]() является потенциальным
является потенциальным
![]() ,
что
,
что
![]()
![]() - ковариантная производная по i-той
координате.
- ковариантная производная по i-той
координате.
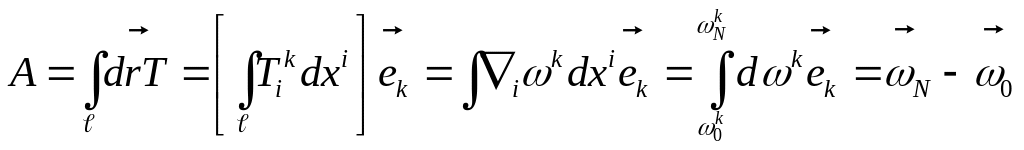
Если векторное или тензорное поле является потенциальным, то скалярный криволинейный интеграл второго рода не зависит от пути интегрирования, а определяется только разность конечной и начальной точки.
Циркуляцией вектора называется
![]()
![]()
Если векторное или тензорное поле является потенциальным, то циркуляция вектора (тензора) равна нулю.
Поверхностный интеграл. Поверхностный интеграл первого рода.
![]()
![]() поверхностный интеграл первого рода.
поверхностный интеграл первого рода.
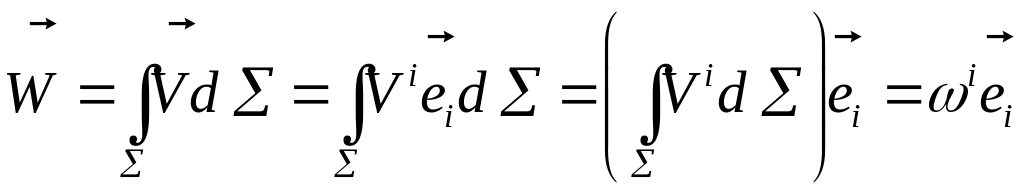
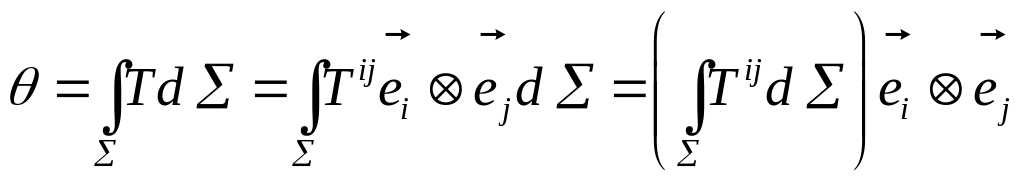
Поверхностные интегралы второго рода.
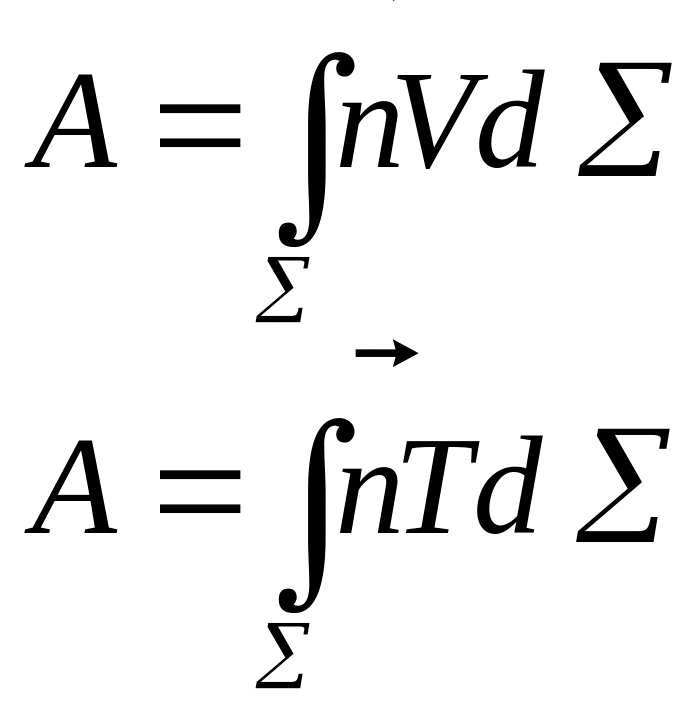 Скалярные
поверхностные интегралы второго рода.
Скалярные
поверхностные интегралы второго рода.
![]()
![]() векторные поверхностные интегралы
второго рода.
векторные поверхностные интегралы
второго рода.
![]() умножим на
умножим на
![]() и просуммируем по
и просуммируем по
![]()
![]() инвариантная формула записи формулы
Стокса.
инвариантная формула записи формулы
Стокса.
Скалярная формула Стокса (1) и (2).
(1)
![]()
(2)
![]()
Векторная формула Стокса.
![]()
![]()
Тензорная формула Стокса
![]()
![]()
Объемные интегралы.
![]()
![]()
![]() для вектора
для вектора
![]() для тензора
для тензора
Формула Гаусса-Остроградского
![]()
![]() - компоненты вектора нормальной
поверхности.
- компоненты вектора нормальной
поверхности.
![]()
![]() - дивергенция
- дивергенция
![]() скалярная формула Гаусса- Остроградского
скалярная формула Гаусса- Остроградского
![]()
Механика
Механика – наука, которая изучает механическое взаимодействие различных материальных объектов.
Механика сплошных сред.
Материальная точка – некоторый физический объект, который обладает тремя степенями свободы.
Абсолютно твёрдое тело – объект, который обладает тремя поступательными и тремя вращательными степенями свободы.
Среднестатистический подход
Феноменологический подход
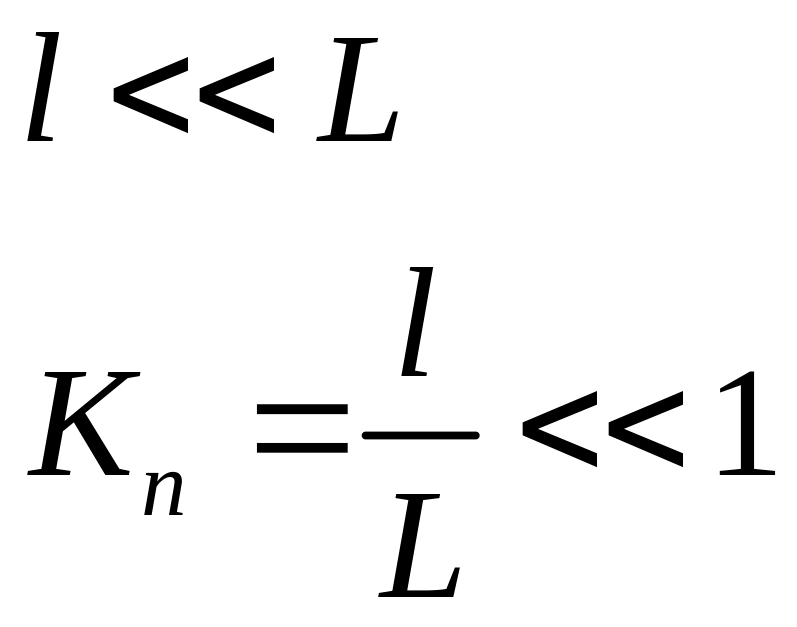 число Кнудсена.
число Кнудсена.
Элементарный объём – это малый объём сплошной среды, в котором все физические величины можно считать однородными, для этого необходимо чтоб размеры элементарного объёма были большого размера и содержать достаточно большое количество атомов ионов, для того, чтобы можно было провести среднестатистическое осреднение.
![]()
![]()
Как накладываем шаг на пространство, так и накладываем шаг на время.
Кинематика сплошных сред. Подход Лагранжа.
![]() ,
где
,
где
![]() - будут выступать в виде некоторого
параметра координаты
носят
название переменные Лагранжа.
- будут выступать в виде некоторого
параметра координаты
носят
название переменные Лагранжа.
![]()
![]()
![]()
![]()
![]()
![]() - контрольный объём.
- контрольный объём.
![]()
![]()
![]()
![]() Эйлерова координата или переменная
Эйлера.
Эйлерова координата или переменная
Эйлера.
Полная производная по времени от величины, заданной в переменных Эйлера.
Процессы, связанные с перемещением называются конвекцией.
![]() Сумма объёмной и конвективной
производных.
Сумма объёмной и конвективной
производных.
Рассмотрим случай, когда производная берётся от векторной величины.
![]()
![]()
Если мы будем рассматривать некоторый тензор второго ранга
![]()
Формула дифференцирования по времени. Интегралы, взятые по подвижному объёму.
![]()
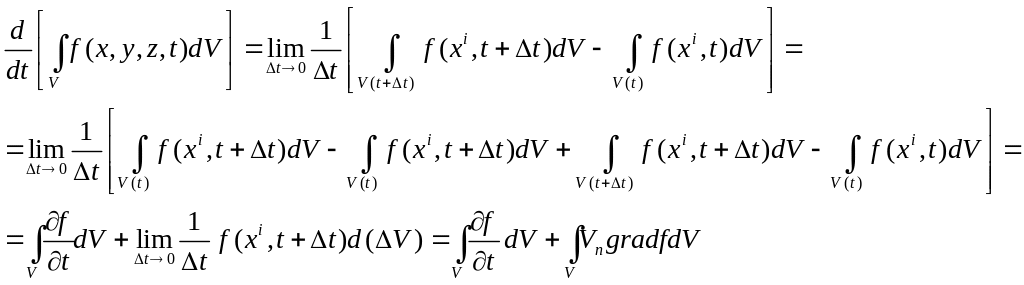
![]()
![]()
Переход от переменных Лагранжа к переменным Эйлера.
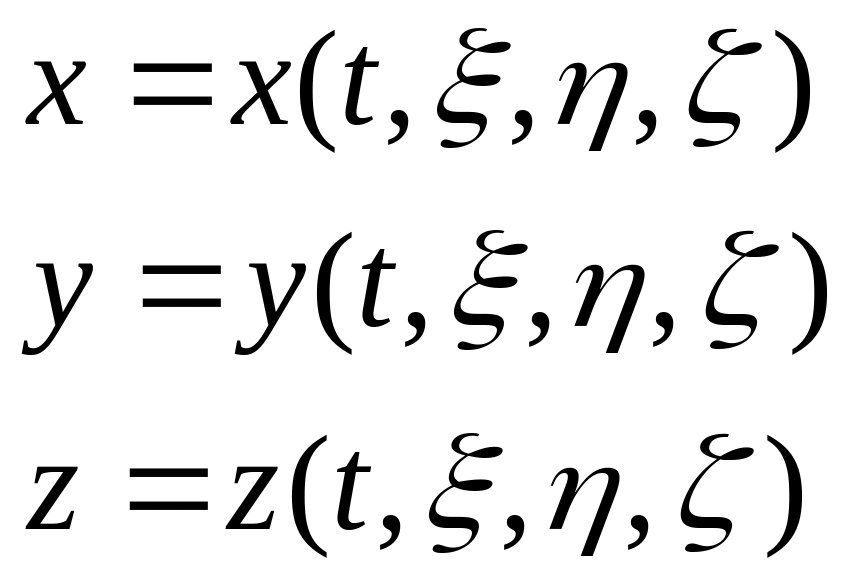 от этих переменных требуется перейти
к переменным Эйлера.
от этих переменных требуется перейти
к переменным Эйлера.
Переход от переменных Эйлера к переменным Лагранжа.
![]()
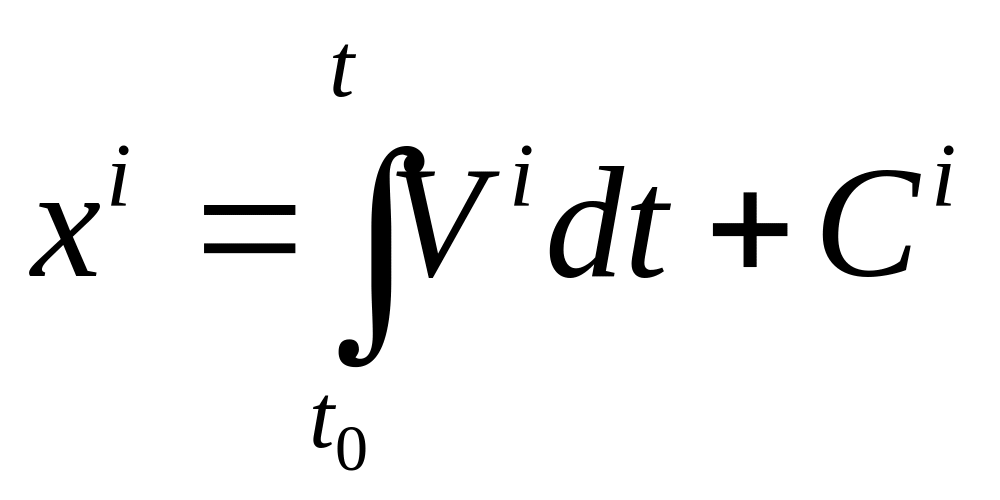
![]() будет задавать положение точки в
начальный момент времени.
будет задавать положение точки в
начальный момент времени.
![]()
При
![]()
![]()
Траектория и линия тока.
Траектория – это линия в пространстве, по которой происходит движение рассматриваемой частицы или тела.
Понятие траектории относится к подходу Лагранжа.
![]() уравнение траектории в дифференциальном
виде.
уравнение траектории в дифференциальном
виде.
![]() - это координаты частицы в заданный
момент времени.
- это координаты частицы в заданный
момент времени.
![]() - время движения частицы.
- время движения частицы.
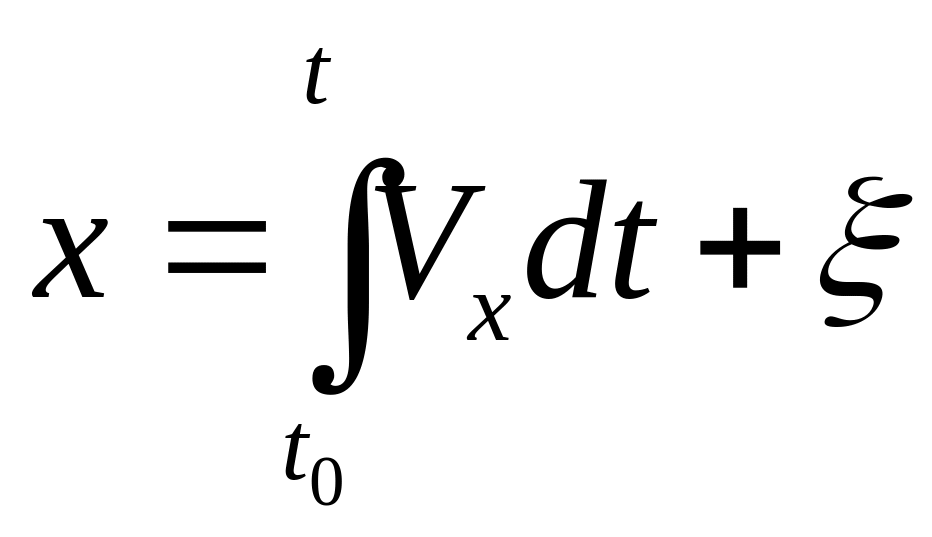
![]()
![]()
![]()
![]()
![]() - уравнение траектории в аналитическом
виде.
- уравнение траектории в аналитическом
виде.
![]() -
это уравнение некоторой пространственной
кривой.
-
это уравнение некоторой пространственной
кривой.
Линия тока – это линия, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.
![]()
![]()
![]() дифференциальное уравнение линии тока.
дифференциальное уравнение линии тока.
- координаты выбранной точки пространства, когда говорят о времени, то имеют в виду время проведения точки в пространстве.
В стационарных задачах линия тока и траектория совпадают.