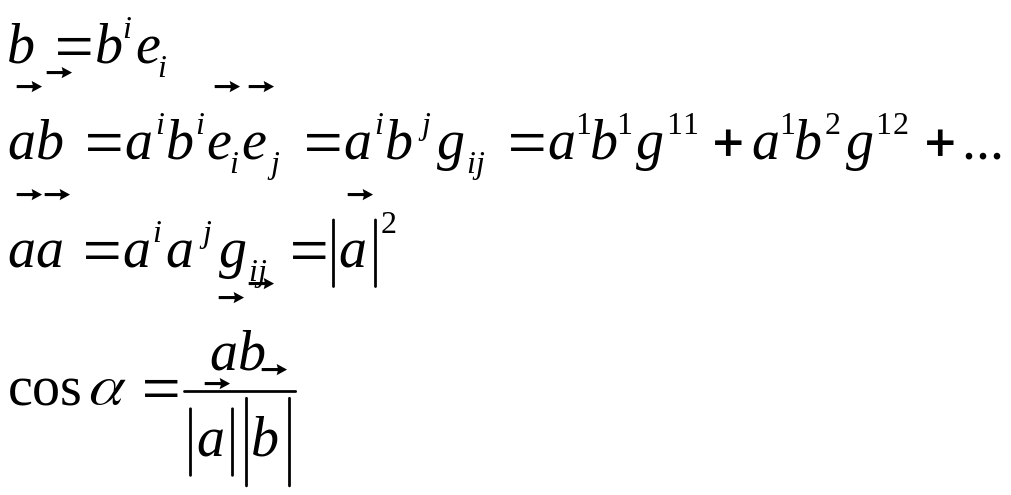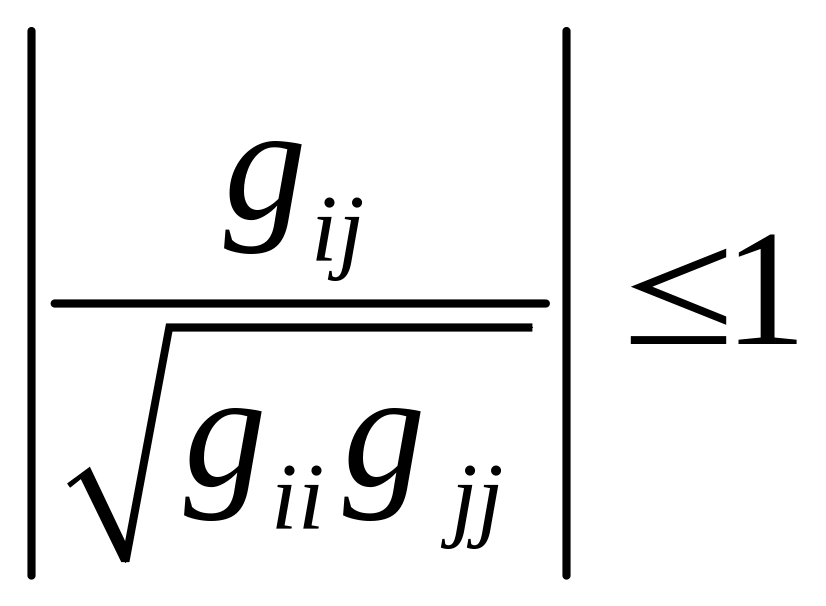Механика сплошных сред. Точечно-векторное аффинное пространство.
Точечно-векторное аффинное пространство представляет собой математическую модель простейших геометрических объектов, на которой базируется теория движения.
Афинно-точечное векторное пространство
есть множество, состоящее из элементов
двух типов – точек и радиус векторов.
Каждые две точки пространств А и В, взятые в определённом порядке, задают вектор
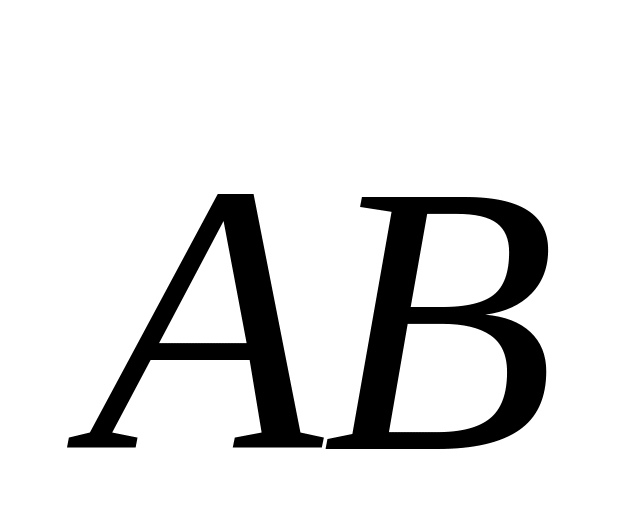.Если задана точка А и радиус-вектор r, то по этой информации мы однозначно можем определить точку В.
Если задано два радиус вектора
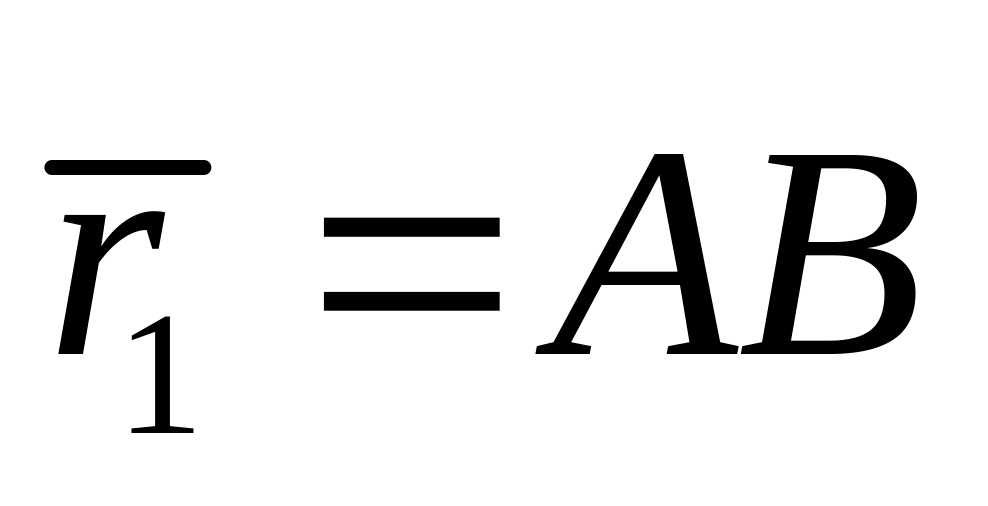и
,
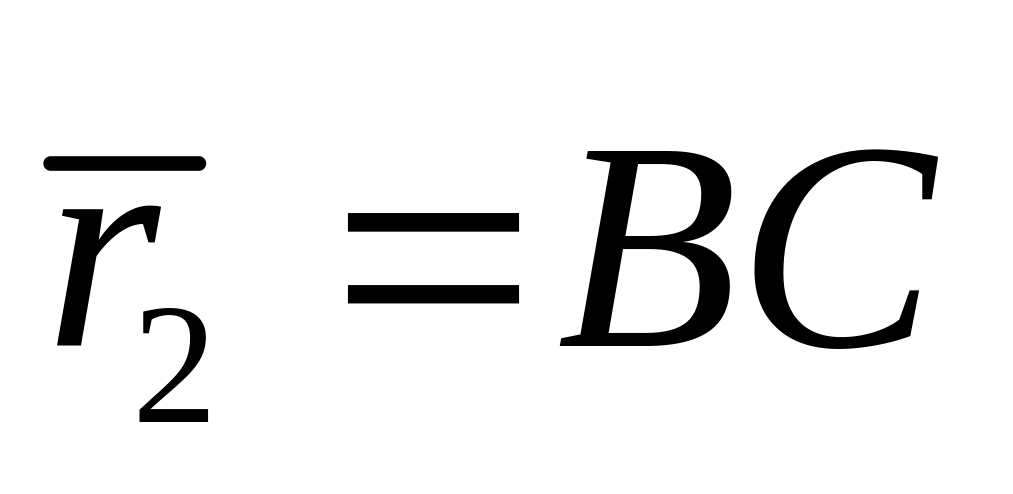то мы можем определить сумму векторов
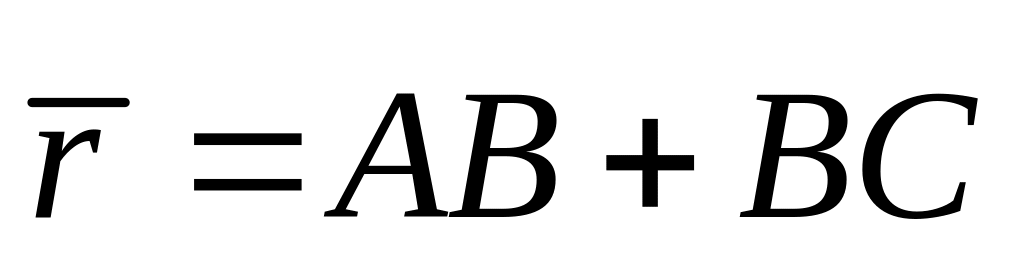
Классификация векторов.
Связные вектора. Характеризуются величиной, направлением и точкой приложения. Для задания такого вектора необходимо задать 6 параметров.
Скользящие вектора. Для задания необходимо задать величину и направление силы, а также линию её действия.
Свободные вектора. Чтобы задать, нужно задать его величину и направление. Точка приложения никакой роли не играет.
Правила сложения свободных векторов.
коммутативность
ассоциативность
существование нулевого вектора
существование обратного вектора
Основные правила умножения вектора на скаляр.
Базисные вектора и системы координат.
уравнение координатной линии.
;
;
базисные вектора заданной системы
координат.
Правая система координат
Цилиндрическая система координат
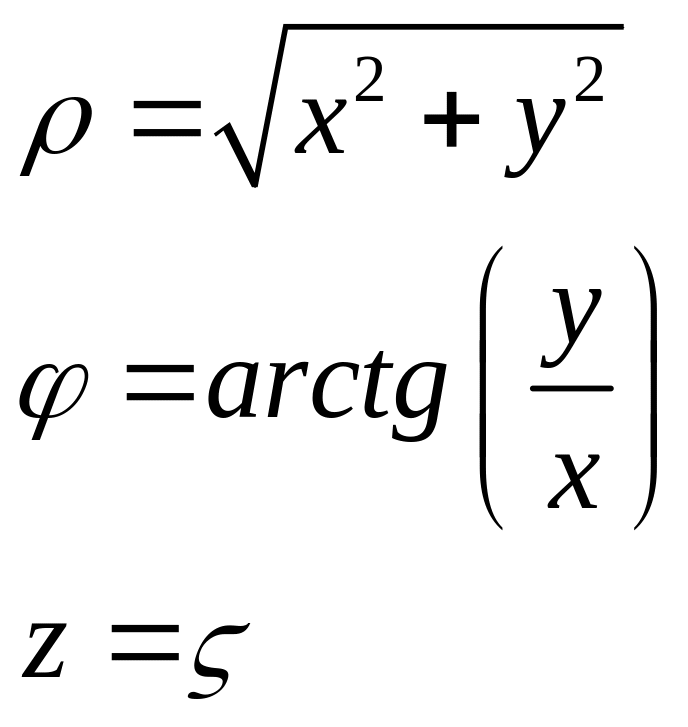
Сферическая система координат
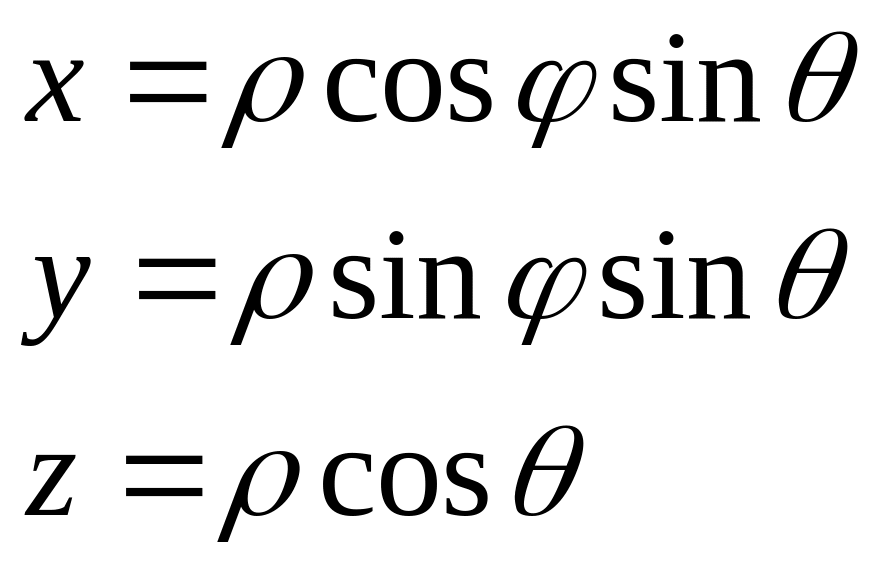
Базисные вектора
Преобразование координат
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
0 |
1 |
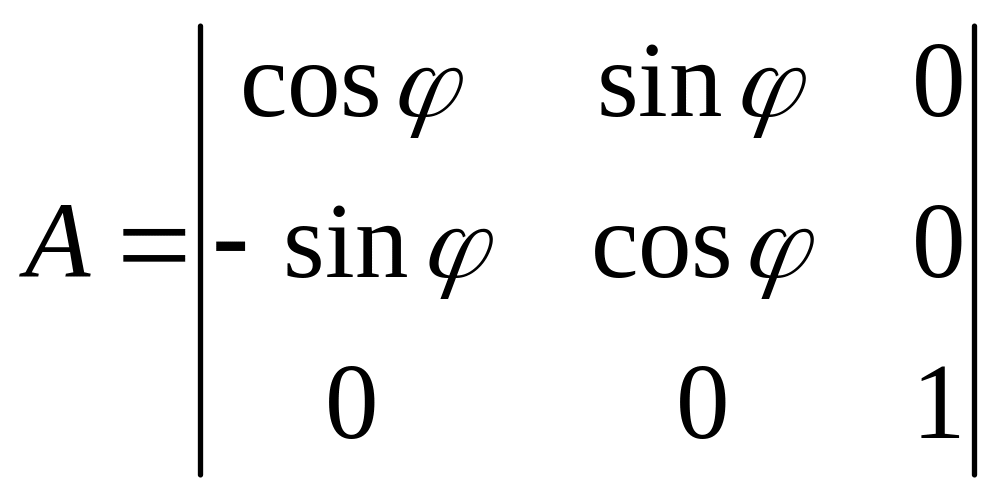матрица прямого преобразования
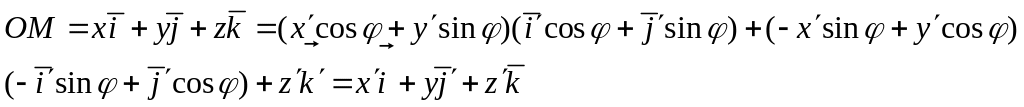
Преобразование осей в общем случае.
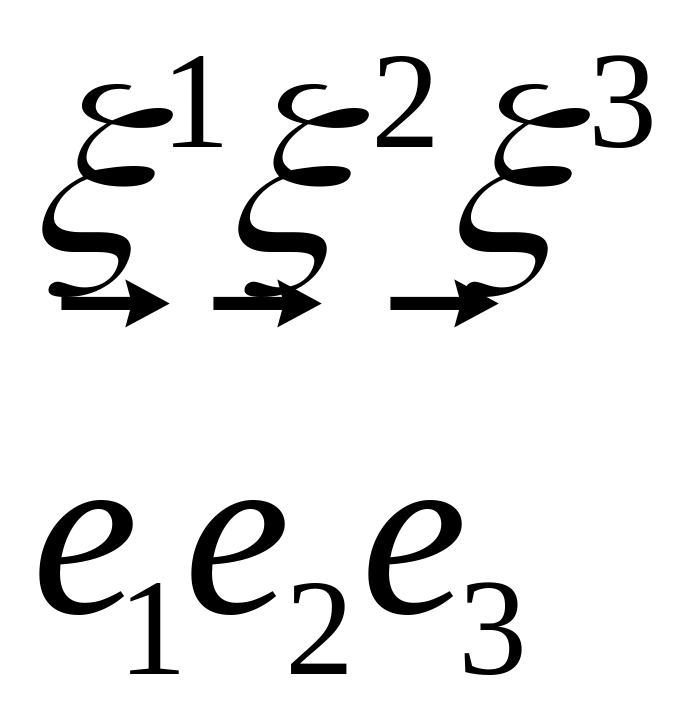- новая система координат
- старая система координат
матрица прямого преобразования.
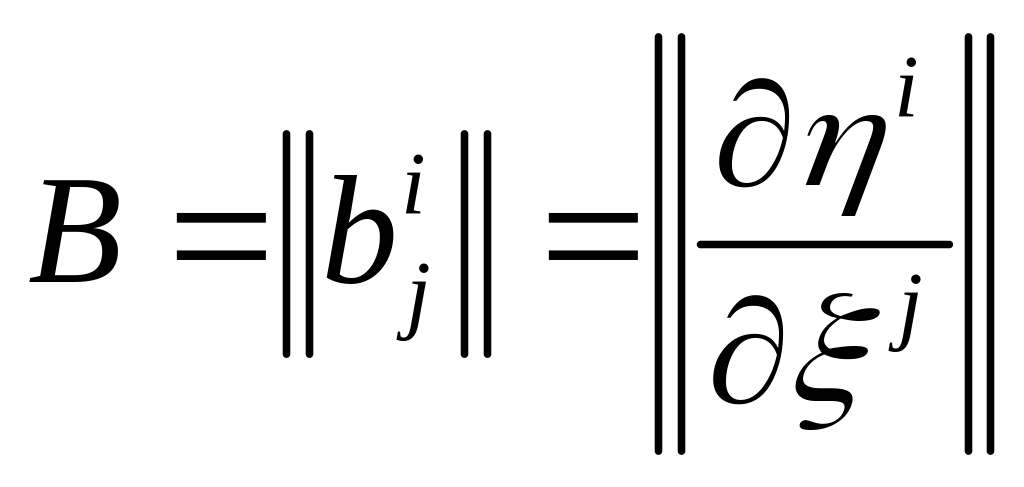
Преобразования, осуществляемые с помощью матриц прямого преобразования называются контравариантными (индекс вверху). Преобразования, осуществляемые с помощью матриц обратного преобразования называются ковариантными (индекс внизу).
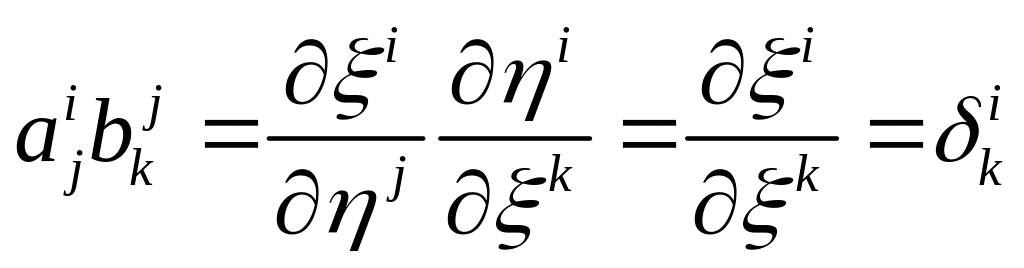- символ Кронекера
Преобразование базисных векторов.
новые координаты,
старые координаты.
Опр. Векторная величина – это объективно существующий физический объект, характеризуемый величиной и направлением, компоненты которого, при повороте координатных осей, преобразуются по тем же правилам, что и координаты направленного объекта.
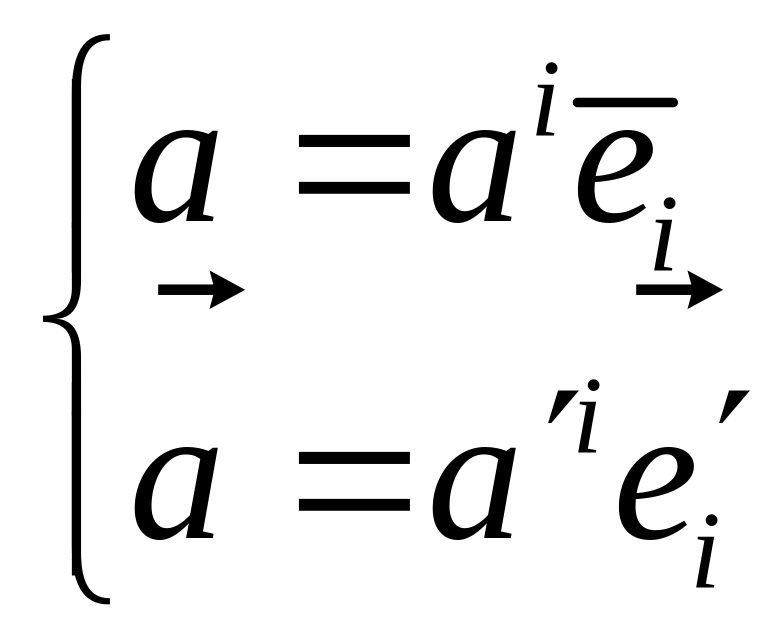
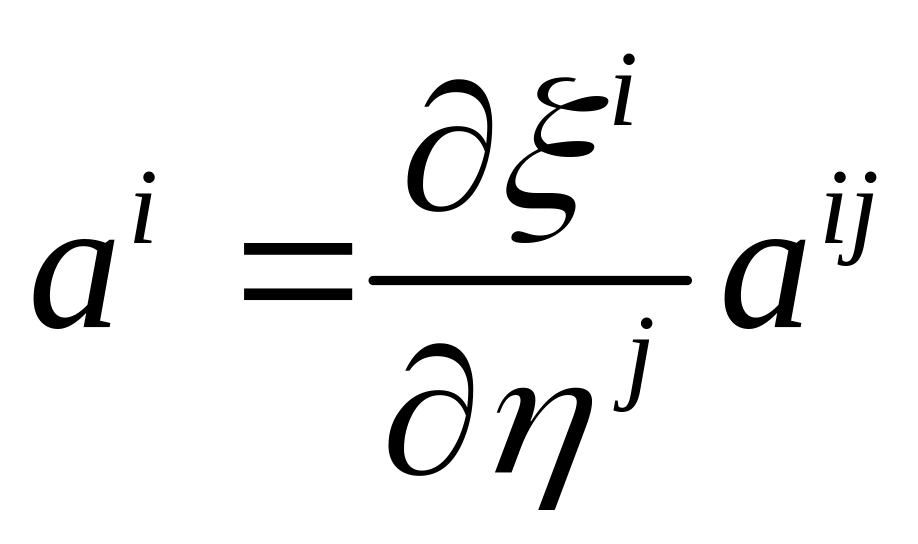это правило преобразования компонент
делает величины векторными.
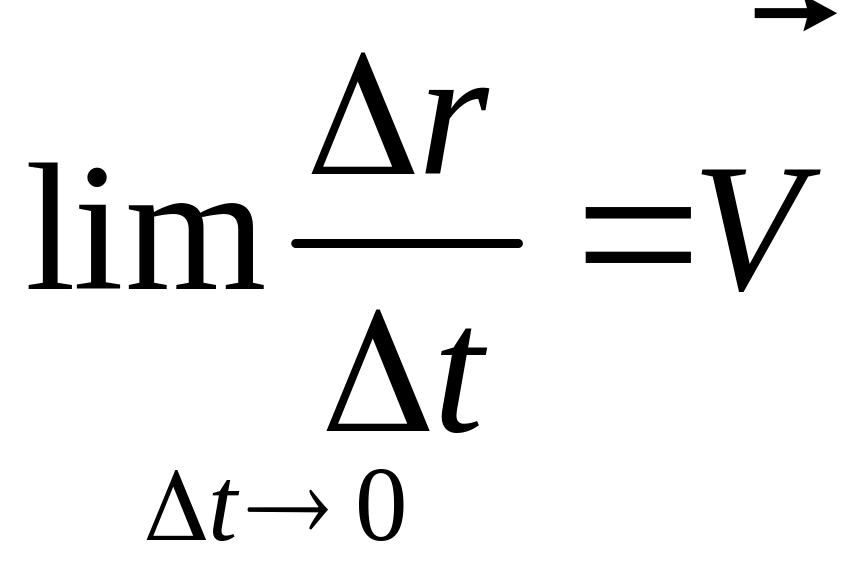
Скалярное произведение векторов.
Введём в соответствие некоторую математическую операцию, которую назовём скалярное произведение, при этом потребуем, чтобы выполнялись некоторые свойства:
при условии, что
;
;
Фундаментальный метрический тензор.
- матрица, определяющая метрику в системе.
Опр. Метрикой пространства называют систему величин, определяющих масштабы единиц, служащих для измерения длин и углов во всех направлениях, в различных точках пространства.
Элементы, лежащие на главной диагонали характеризуют масштабы длин.
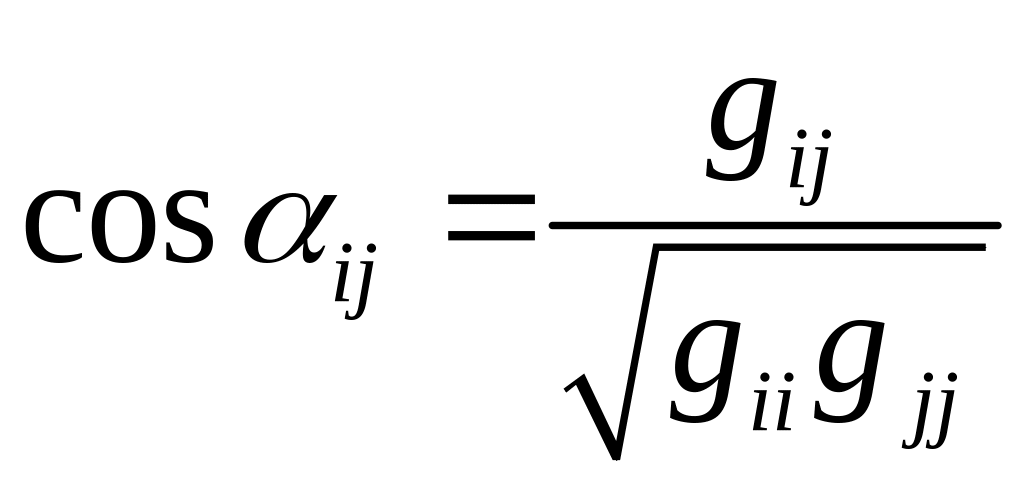
В качестве первого ограничения, ставим условие:
Для того, чтобы из трёх положительных углов можно было построить трёхгранник, необходимо, чтобы любые 2 угла, каждый из которых < 180 в сумме были бы больше третьего, а их разность была меньше третьего.
определитель матрицы 3-го порядка
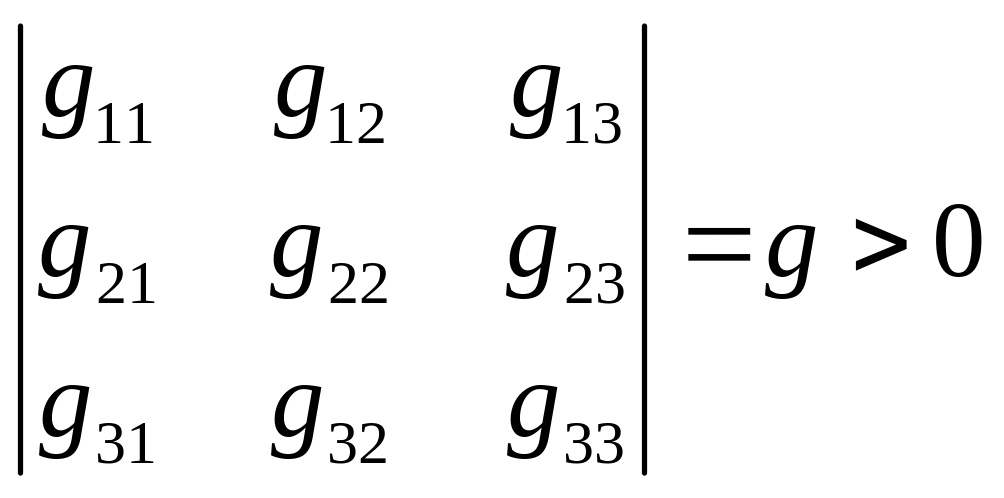
для того, чтобы условие выполнялось, необходимо, чтобы матрица была положительно определённой. Называют фундаментальным метрическим скаляром.
;
При преобразовании координат компоненты метрического тензора преобразуются как произведение координат. Скалярное произведение векторов, записанное с использованием компонент метрического тензора.
