3. Шекті (ақырлы) жиынның анықтамасы

X жиыны шекті деп аталады, егер биекциясы бар болса, яғни Х жиынын {1,2,…,n} натурал қатарлы кесіндіге өзара бір мәнді бейнелеуге болады; сонымен қатар X= n.

Құр жиынды шекті жиындарға жатқызу келісілген және оны =0 деп белгілейді.

Бұндай биекцияны орнату мүмкін болмайтын барлық жиындарды шексіз(ақырсыз) деп атайды.

Ақырлы жиындардың қасиеттері

Ақырлы жиындардың қасиеттерін теоремалар түрінде құрастырайық. (барлық теоремалар қатаң дәлелденбейді) Теорема (қосынды ережесі). Айталық Х жиыны қиылыспайтын ақырлы жиындардың r бірігуі болсын. Онда .

Теореманың шарты бойынша жиындар жүйесі Х жиынының бөліктеуі болып табылады. Дәлелдеуді бөліктеу блоктары r саны бойынша математикалық индукция әдісі бойынша жүргіземіз.

1 қадам. Теорема болғанда орындалатындығын дәлелдейік. Айталық  және жиындары ақырлы болсын, яғни және биекциялары бар болады. биекциясын келесі тәсілмен орнатайық: жиынының барлық элементерінің бұрынғы нөмірлерін қалтырайық, ал жиынының элементтерін санына арттырайық. Алынған бейнелеу және -нің биективтілігінен биекция болып табылады.

Бұдан . Индукцияның негізі дәлелденді.

2 қадам . Индукциялық өтудің негізі мынада: теорема бөліктеу блоктарының санында орындалсын деп болжайық; бұл жағдайда оның блоктардың саны r болғанда да дұрыс болатындығын дәлелдейік.

Тұжырымдама: , жиындары ақырлы және Y жиынының бөліктеуін құрайды. Онда

X жиынының r ақырлы жиындарға бөліктеуін қарастырайық. Онда бірігудің ассоциативтілік қасиетінен шығады. деп белгілейік. Индукцияның негізіне сүйене отырып (1 қадам) аламыз, ал индукциялық тұжырым бойынша Сонымен индукциялық өту дәлелденді.

Қорытынды. Математикалық индукция әдісі бойынша теорема кез келген бөліктеу блогының натурал r санында орындалады.

Теорема (көбейту ережесі). Айталық Х ақырлы жиыны ақырлы жиындардың r декарттық көбейтіндісі түрінде келтірілген. Онда .

Көбейту ережесі қосу ережесіне ұқсас математикалық индукция бойынша дәлелденеді.

Теорема (енгізу және шығару ережесі). Айталық және ақырлы жиындар болсын. Онда .

Теореманың дәлелдеуі қосу ережесіне сүйенеді. жиынын қиылыспайтын жиындардың бірігуі түрінде жазайық , мұндағы , , (1.21 сурет). Онда қосынды ережесі бойынша , алайда , сондықтан , . аламыз, бұдан .

Теорема (енгізу-шығарудың жалпыланған ережесі).

Айталық X ақырлы жиыны ақырлы жиындардың r бірігуі болсын. Онда

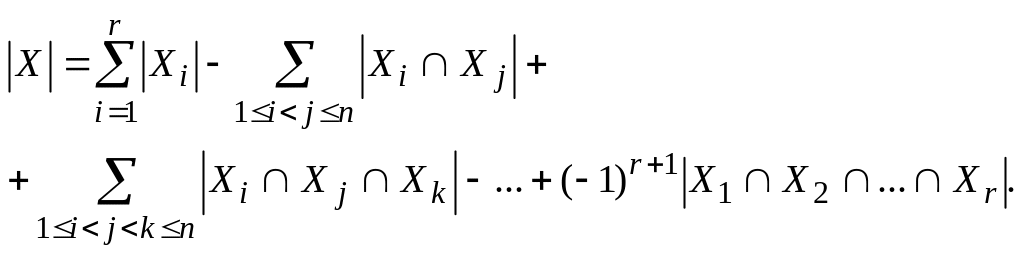
Теорема (ақырлы жиындардың булеанының қуаты жайлы). Айталық X жиыны ақырлы және X=n болсын. Онда B(X)= .

Х жиынының булеаны B(X) болатындығын ескерте кетейік, яғни Х жиынының барлық ішкі жиындарының жиыны. (1.1.6 қараңыз). Теореманы Х жиынының элементтерінің n саны бойынша математикалық индукция әдісімен дәлелдейік. Индукцияның негізі:. n=1 болғанда теореманың дұрыстығын дәлелдеік. X жиыны бір элементтен тұратындықтан, онда Х жиынының барлық мүмкін ішкі жиындарының саны екеу болады: құр жиын және Х жиынының өзі, яғни B (X) .

Индукциялық өту. Айталық теорема X= болғанда орындалсын. Кез келген бір жиынын қарастырайық және оның барлық ішкі жиындары болатындығын көрсетейік.

Покрасим элемент множества X жиынының элементін «жасыл» түске бояйық, және Х жиынының барлық ішкі жиындарын әдемі деп, ал құрамында бұл элементтері болмаса әдемі емес деп атайық. Индукциялық тұжырым бойынша әдемі емес ішкі жиындардың саны тең. Әдемі ішкі жиындар әдемі емес ішкі жиындарға кезекппен «жасыл» элементті қосу арқылы алынады, ендеше олардың саны да тең. Қосынды ережесі бойынша Х жиынының барлық ішкі жиындарының саны тең.

Қорытынды. Математикалық индукция әдісі бойынша теорема кез келген натурал n саны үшін орындалады.