2. Практическая часть

   1. Описание программы

Построена компьютерная модель цепи Маркова с частичными связями и переменным шаблоном со следующими входными параметрами:

• глубина предыстории однородной цепи Маркова ЦМ .

• длина временного ряда с пространством состояний .

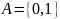• Шаблоны 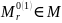и 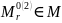, которые повторяются с периодом

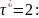
• Стохастическая матрица вероятностей одношаговых переходов для шаблонов:

В частном случае, при данная матрица имеет следующий вид:

Реализовано моделирование цепи Маркова с частичными связями и переменным шаблоном, построение оценок максимального правдоподобия матрицы вероятностей одношаговых переходов и переменного шаблона на основе смоделированного временного ряда. Далее более подробно рассматривается алгоритм работы программы.

2. Моделирование временного ряда длительности

Пользователем задаются первые элементов последовательности. Для моделирования элементов с нечетными номерами выбирается шаблон . Рассматривается -предыстория элемента. Распределениями вероятностей исхода для данных элементов являются строки матрицы , соответствующие состояниям предыдущих элементов

В частности, если предыстория элемента имеет вид

,

то, например, при

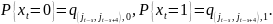
Элементы с четными номерами моделируются аналогичным образом с использованием шаблона

На каждом шаге моделирование происходит с помощью генератора псевдослучайных чисел [3], работающего по следующему алгоритму:

1. Генерируется число в диапазоне .

2. 

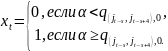
В результате имеется временной ряд , где пространство состояний – конечное множество мощности .

3. Построение оценок максимального правдоподобия и

Логарифмическая функция правдоподобия имеет вид:

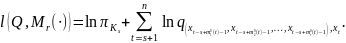
Задача на условный экстремум:

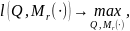
Поиск условной оценки максимального правдоподобия матрицы одношаговых переходов осуществляется путем приравнивания к нулю компонент градиента логарифмической функции правдоподобия:

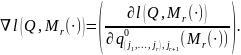
Используя факт, что матрица стохастическая,

, условная оценка полностью определяется шаблоном

Для вычисления оценки шаблона при известном истинном значении числа связей можно воспользоваться алгоритмом полного перебора 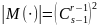значений логарифмической функции правдоподобия.

В частности, при имеется следующая система уравнений:

где частота выпадения при предыстории .

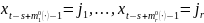Условной оценкой максимального правдоподобия является решение данной системы:

.

Логарифмическая функция правдоподобия перепишется в следующей форме:

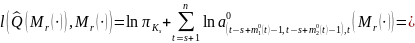
Оценка максимального правдоподобия ищется путем перебора вариантов шаблонов. Производится подсчет частот при всевозможных вариантах пар шаблонов и выбирается та пара, которая максимизирует логарифмическую функцию правдоподобия. Таким образом:

Оценка максимального правдоподобия матрицы имеет вид: