МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

НИИ прикладных проблем математики и информатики

ОЦЕНКА ПАРАМЕТРОВ ДЛЯ МОДЕЛИ ЦМ С ПЕРЕМЕННЫМ ШАБЛОНОМ

Отчет по НИР № 36/1

Батуры Олега Владимировича,

сотрудника НИИ ППМИ

Научный руководитель:

доктор физ.-мат. наук,

заведующий кафедрой ММАД

Ю. С. Харин

Минск, 2015

СОДЕРЖАНИЕ

Введение 2

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 3

1.1 Цепь Маркова с частичными связями и переменным шаблоном 3

1.2 Статистическое оценивание параметров ЦМ с переменным шаблоном 4

1.3 Алгоритмы вычисления оценки шаблона 8

1.4 Алгоритмы вычисления оценки функции 10

2. ПРАКТИЧЕСКАЯ ЧАСТЬ 11

2.1. Описание программы 11

2.2. Моделирование временного ряда длительности 12

2.3. Построение оценок максимального правдоподобия и 13

2.4. Результаты экспериментов 16

2.5. Вывод 19

Заключение 20

Список использованной литературы 21

Введение

При математическом моделировании сложных систем и процессов в различных научных сферах часто возникает необходимость построения вероятностно-статистических моделей дискретных временных рядов 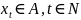, где пространство состояний 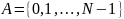— конечное множество мощности 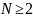с длинной памятью [1]. Известной моделью таких дискретных временных рядов является цепь Маркова достаточно высокого порядка , определяющего длину памяти; если 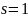, то цепь Маркова называется простой, если 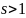— сложной. Однако для такой модели число параметров 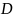растет экспоненциально при увеличении порядка : , и для статистического оценивания параметров требуется иметь реализацию 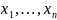не всегда доступной на практике длительности . В связи с этим актуальна проблема построения малопараметрических моделей цепей Маркова высокого порядка. В данной работе исследуется малопараметрическая модель цепи Маркова порядка с частичными связями ЦМ , рассмотренная в [2], для которой шаблон связей 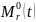зависит от функции, определяющей его изменение во времени, исследуются ее вероятностные характеристики, строятся статистические оценки параметров модели.

1. Теоретическая часть

1. Цепь Маркова с частичными связями и переменным шаблоном

По аналогии с [2] построим модель цепи Маркова с частичными связями и переменным шаблоном.

Пусть – однородная ЦМ( ), заданная на вероятностном пространстве ( ). Рассмотрим обобщение данной модели, когда шаблон 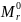зависит от времени :

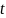причем:

В общем случае шаблон зависит от некоторой функции 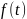, определяющей его изменение. Простейшая модель такой зависимости – периодическая функция с некоторым периодом :

.

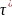При произвольной модели зависимости шаблона от времени -мерное распределение вероятностей имеет вид:

Лемма 1. Случайная последовательность является неоднородной ЦМ порядка с частичными связями и 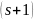-мерной матрицей вероятностей одношаговых переходов в момент времени

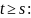
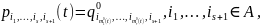
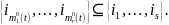
1.2 Статистическое оценивание параметров цм с переменным шаблоном

Для статистического оценивания параметров ЦМ( ) с переменным шаблоном будем пользоваться методом максимального правдоподобия.

Рассмотрим задачу построения оценок максимального правдоподобия (ОМП) для параметров шаблона и стохастической матрицы по наблюдаемой реализации длительности .

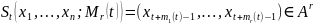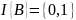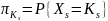Введем обозначения, пусть – мультииндекс -го порядка; – функция, которую условимся называть селектором -го порядка с параметрами и – индикатор события ; – начальное -мерное распределение вероятностей ЦМ ;

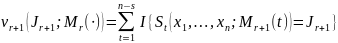
– частота 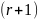-граммы для шаблона , удовлетворяющая условию нормировки:

Лемма 2. Для модели ЦМ с переменным шаблоном логарифмическая функция правдоподобия имеет вид:

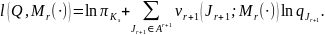
В частности, когда имеется лишь 2 возможных шаблона связей , а закон изменения шаблона во времени задается некоторой функцией 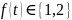, то есть , логарифмическая функция правдоподобия запишется в виде

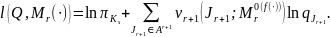
Для того, чтобы найти ОМП для матрицы при известной функции шаблона 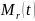, необходимо решить задачу на условный экстремум:

В результате получаем условную ОМП для матрицы ( ):

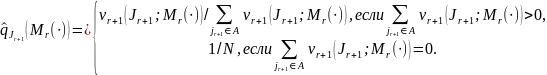
Далее рассмотрим задачу построения ОМП для шаблона при известной функции смены шаблона такой, что .

Пусть существует стационарное распределение вероятностей ЦМ с переменным шаблоном . Допустим, что модель стационарна (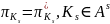 ), тогда распределение вероятностей 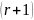-граммы в момент времени для шаблона будет иметь следующий вид:

Соответствующая частотная оценка вероятностей :

.

Энтропия -мерного распределения вероятностей запишется в виде:

Количество информации по Шеннону, содержащейся в -грамме о будущем символе :

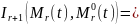
С учетом принятых обозначений логарифмическая функция правдоподобия для оценки имеет следующий вид:

где 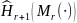– подстановочная оценка энтропии, получающаяся при подстановке вместо истинных значений их оценок { }.

Учитывая, что 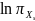не зависит от , добавляя также не зависящее от слагаемое 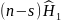, а также используя тот факт, что:

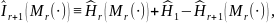
приходим к следующей ОМП шаблона :

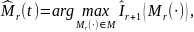
где 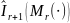– подстановочная оценка количества информации по Шеннону, получающаяся при подстановке вместо истинных значений их оценок { }.

Пусть – некоторый класс функций, которому принадлежит функция изменения шаблона во времени. Предположим, что все возможные значения шаблона известны. Тогда ОМП функции выглядит следующим образом: