1. Определение первообразной и неопределенного интеграла. Определение . Функция F(x) называется первообразной для функции f(x) на промежутке X, если (F(x))/ = f(x) ∀ x ∈ X. Теорема 1. Если F1(x) и F2(x) − две любые первообразные для f(x) на X, то F2(x) − F1(x) = C (C = const). Следствие . Если F(x) − одна из первообразных для f(x) на X, то любая другая первообразная Ф(x) для функции f(x) на X имеет вид Ф(x) = F(x) + C, где C − некоторая постоянная. Определение . Совокупность всех первообразных для функции f(x) на X называется неопределенным интегралом от функции f(x) на промежутке X и обозначается ∫ f(x)dx. В силу следствия из теоремы 1 ∫ f(x)dx = F(x) + С, где F(x) − одна из первообразных для f(x), C − произвольная постоянная. (Иногда символом ∫ f(x)dx обозначается не вся совокупность первообразных, а какая-либо одна из них.)

Основные свойства неопределенного интеграла. 1°. d ∫ f(x) dx = f(x) dx. 2°. ∫ dF(x) =F(x) + C. 3°. Линейность интеграла. Если существуют первообразные функций f(x) и g(x), а α и β − любые вещественные числа, то существует первообразная функции αf(x) + βg(x), причем ∫ [αf(x) + βg(x)]dx = α ∫ f(x)dx + β ∫ g(x)dx.

Таблица основных неопределенных интегралов. I.∫ 0 dx = C. II. ∫ 1 dx = x + C. III. ∫ x dx α = + C (α ≠ −1). IV. ∫ dx = ln |x| + C. (x ≠ 0). V. ∫ ax dx = + C (0 < a ≠ 1), ∫ e x dx = e x + C. VI. ∫ sin x dx = −cos x + C. VII. ∫ cos x dx = sin x + C. VIII. ∫ = tg x + C (x ≠ π/2 + πn, n ∈ Z). IX. ∫ = −ctg x + C (x ≠ πn, n ∈ Z). X. ∫ = arcsin x + C, −arccos x + C (− 1 < x < 1). XI. ∫ = arctg x + C, −arcctg x + C. XII. ∫ = ln |x + | + C. XIII. ∫ = + C (x ≠ ±1). XIV. ∫ sh x dx = ch x + C. XV. ∫ ch xdx = sh x + C. XVI. ∫ = th x + C. XVII. ∫ = −cth x + C.

2. Интегрирование по частям. Теорема 3 . Пусть на промежутке X функции u(x) и v(x) дифференцируемы и существует v(x)u'(x) dx (т. е. функция v(x)u'(x) имеет первообразную на X). Тогда u(x)v'(x) dx также существует на X и ∫ u(x)v'(x) dx = u(x)v(x) − ∫v(x)u'(x) dx. Это равенство называется формулой интегрирования по частям. Так как u'(x) dx = du, v'(x) dx = dv, то эту формулу можно записать в виде ∫ udv = u(x)v(x) − ∫ vdu.

Метод интегрирования по частям удобно применять в следующих случаях. 1. Подынтегральное выражение содержит в виде множителя функции ln x, ln ϕ(x), arcsin x, arccos x, arctg x. Если в качестве u(x) выбрать эти функции, то подынтегральное выражение vdu нового интеграла обычно получается проще исходного. 2. Подынтегральная функция имеет вид P(x) e ax, P(x) sin ax, P(x) cos ax, где P(x) − многочлен относительно переменной x. Если в качестве u(x) выбрать P(x), то в новом интеграле подынтегральная функция снова принадлежит одному из указанных типов, но степень многочлена окажется уже на единицу меньше. Выбирая этот многочлен снова в качестве u(x), понижаем степень еще на единицу и т. д. 3. Подынтегральная функция имеет вид e ax sin bx, e ax cos bx, sin(ln x), cos(ln x) и т. п. После двукратного интегрирования по частям получается снова исходный интеграл с некоторым коэффициентом. Полученное равенство является линейным алгебраическим уравнением относительно искомого интеграла P_n(x) Q_m(x) R_k(x)

3. Интегрирование рациональных функций. 1. Разложение рациональной дроби на сумму простых дробей. Рассмотрим рациональную функцию (или рациональную дробь) Pn(x)/Qm(x). Здесь Pn(x) и Qm(x) − многочлены степеней n и m относительно переменной x. Если n ≥ m, т. е. дробь неправильная, то ее можно представить в виде

= Pn − m(x) + (k < m), или, как говорят, выделить из нее целую часть Pn − m(x). В результате интегрирование неправильной рациональной дроби сводится к интегрированию правильной дроби Rk(x)/Qm(x). Теорема 4 . Пусть Pn(x)/Qm(x) − правильная рациональная дробь (n < m), а разложение знаменателя дроби Qm(x) на произведение неприводимых вещественных множителей имеет вид Qm(x) = (x − a) α … (x − b) α (x 2 + px + q) γ … (x 2 + rx + s) δ , где a, …, b − вещественные корни, x 2 + px + q, …, x 2 + rx + s − квадратные трехчлены, не разложимые на вещественные множители. Тогда

(1)

где Ai, Bi B , Mi, Ni, Ki, Li − вещественные числа.

Дроби, входящие в правую часть (1), называются простыми, а само равенство (1) называется разложением правильной рациональной дроби Pn(x)/Qm(x) на сумму простых дробей с вещественными коэффициентами.

2. Интегрируемость простых дробей в элементарных функциях. Каждая из простых дробей интегрируется в элементарных функциях:

Интеграл Kα вычисляется по рекуррентной формуле (см. § 4).

4. Интегрирование тригонометрических функций. Интеграл вида ∫ R(sin x, cos x) dx рационализируется с помощью универсальной тригонометрической подстановки t = tg(x/2). На практике она приводит часто к громоздким выкладкам. В ряде случаев более удобны другие подстановки:

а) t = cos x, если R(−sin x, cos x) = −R(sin x, cos x); б) t = sin x, если R(sin x, −cos x) = −R(sin x, cos x); в) t = tg x, если R(−sin x, −cos x) = R(sin x, cos x).

5. Неопределенный интеграл: интегрирование иррациональных функций.

1. Интегрирование простейших иррациональных функций

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

Наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена

Основным приемом интегрирования таких функций будет метод замены переменной. Будем искать такие подстановки, которые привели бы подынтегральное выражение к рациональному виду. Назовем этот прием методом рационализации подынтегрального выражения.

Рассмотрим класс интегралов 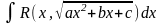, где R – рациональная функция двух аргументов, a, b, c – действительные числа.

Предполагаем, что квадратный трехчлен не имеет равных корней, так что корень из него не может быть заменен рациональным выражением.

Теорема: Интеграл вида 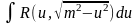подстановкой или

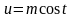сводится к интегралу от рациональной функции относительно sin t или cos t.

Пример 1:

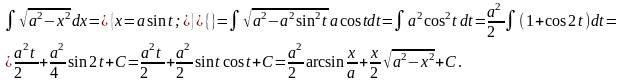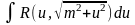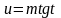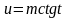Теорема: Интеграл вида подстановкой или сводится к интегралу от рациональной функции относительно sin t и cos t.

Пример 2:

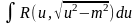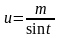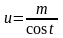Теорема: Интеграл вида подстановкой или сводится к интегралу от рациональной функции относительно sin t или cos t.

Пример 3:

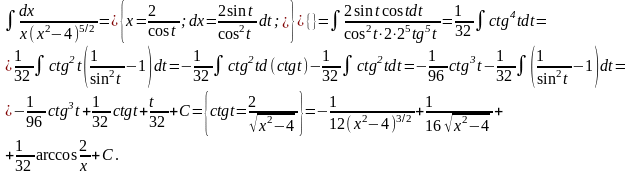
2 способ. Подстановки Эйлера. (1707-1783)

Рассмотрим три подстановки Эйлера, с помощью которых всегда можно достигнуть рационализации подынтегрального выражения.

1. Если . Тогда делают такую замену: .

Возводя это равенство в квадрат, найдем 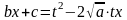, так что

, ,

.

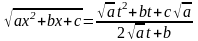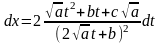Для определения получается уравнение первой степени, так что , а одновременно с ним также и радикал , выражается рационально через .

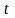Если полученные выражения подставить в , то вопрос сведется к интегрированию рациональной функции от . В результате, возвращаясь к , нужно будет положить

.

2. Если . В этом случае можно положить .

Если возвести в квадрат, уничтожить 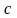в обеих частях и сократить на , то получим 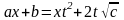- снова уравнение первой степени относительно . Отсюда

, ,

.

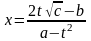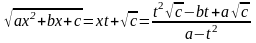Подставив это в , очевидно, осуществим рационализацию подынтегрального выражения. Проинтегрировав, в результате положим

.

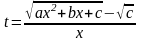3. Если квадратный трехчлен имеет различные вещественные корни  и . Тогда этот трехчлен, как известно, разлагается на линейные множители .

Положим 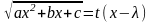, (или ).

Возводя в квадрат и сокращая на 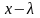, получим и здесь уравнение первой степени, так что

, , .

Таким образом, интегралы данного класса всегда берутся в конечном виде, причем для представления их, кроме функций, через которые выражаются интегралы рациональных функций, нужны еще лишь квадратные корни.

Отметим, что подстановки Эйлера неудобны для практического использования, т.к. даже при несложных подинтегральных функциях приводят к весьма громоздким вычислениям. Эти подстановки представляют скорее теоретический интерес.

2. Метод неопределенных коэффициентов

Рассмотрим интегралы следующих трех типов:

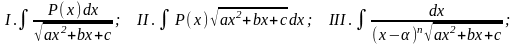
где P(x) – многочлен, n – натуральное число.

Причем интегралы II и III типов могут быть легко приведены к виду интеграла I типа.

Далее делается следующее преобразование:

в этом выражении Q(x)- некоторый многочлен, степень которого ниже степени многочлена P(x), а  - некоторая постоянная величина.

Для нахождения неопределенных коэффициентов многочлена Q(x), степень которого ниже степени многочлена P(x), дифференцируют обе части полученного выражения, затем умножают на и, сравнивая коэффициенты при одинаковых степенях х, определяют  и коэффициенты многочлена Q(x).

Данный метод выгодно применять, если степень многочлена Р(х) больше единицы. В противном случае можно успешно использовать методы интегрирования рациональных дробей, рассмотренные выше, т.к. линейная функция является производной подкоренного выражения.

Пример 1.

.

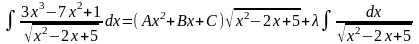Теперь продифференцируем полученное выражение, умножим на и сгруппируем коэффициенты при одинаковых степенях х.

=

=

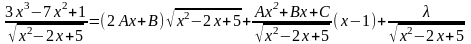
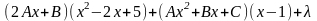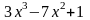
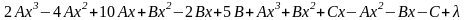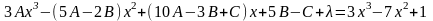
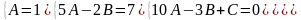
Итого: =

=

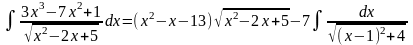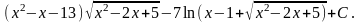
Пример 2.

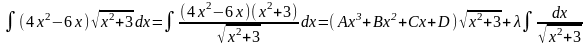
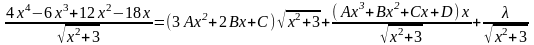
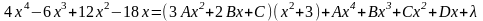
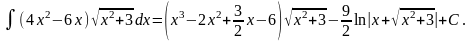
Пример 3.

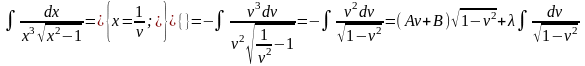
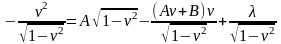
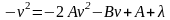
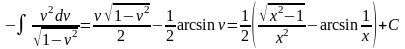
Второй способ решения того же самого примера.

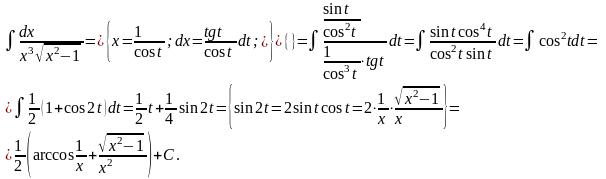
С учетом того, что функции arcsin и arccos связаны соотношением 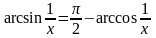, а постоянная интегрирования С – произвольное число, ответы, полученные различными методами, совпадают.

Как видно, при интегрировании иррациональных функций возможно применять различные рассмотренные выше приемы. Выбор метода интегрирования обуславливается в основном наибольшим удобством, очевидностью применения того или иного метода, а также сложностью вычислений и преобразований.

Пример 4.