3.1.2 Проверочный расчёт быстроходной передачи по напряжениям изгиба
Выполняем проверочный расчёт передачи по напряжениям изгиба по формуле:
, (3.4)
где 
- коэффициент
формы зуба;
‑ окружное
усилие на зубчатом колесе, Н;
‑ коэффициент
расчётной нагрузки.
– опытный
коэффициент, характеризующий понижение
прочности зубьев конической передачи
по сравнению с цилиндрической;
Коэффициент
определяем по рекомендациям [3].
При
и
(3.5)
Коэффициент
выбирается по графику рисунок 8.20, [3]
в зависимости от эквивалентного числа
зубьев колеса и коэффициента смещения
Эквивалентное число зубьев для конических колес с косыми зубьями определяется по формуле
(3.6)
Тогда для шестерни
По рисунку 8.20, [3] при коэффициенте смещения x = 0:
для шестерни при
числе зубьев
;
для колеса при
числе зубьев
;
Для колеса и для
шестерни находим отношение
Для шестерни
Для колеса
Дальнейший расчёт ведем по наименьшему значению, т.е по колесу.
Коэффициент расчётной нагрузки определяем по формуле:
, (3.7)
где 
‑ коэффициент
концентрации нагрузки (выбирается по
графикам рисунок 8.15, [3]);
‑ коэффициент
динамической нагрузки (выбирается по
таблице 8.3, [3]).
Коэффициент
определяется по формуле
(3.8)
По таблице 8.3, [3]
при степени точности колес – 8, и
окружной скорости
м/с
выбираем
= 1,06.
Тогда коэффициент расчётной нагрузки:
.
Окружное усилие
на шестерне
,
Н определяем по формуле:
, (3.9)
Н
Напряжения изгиба в передаче
МПа
252 МПа
Условие изгибной прочности соблюдается.
Определяем радиальное усилие в зацеплении по формуле
(3.10)
Н
Определяем осевое усилие в зацеплении по формуле
(3.11)
Н
3.2 Проверочный расчёт тихоходной передачи редуктора
3.2.1 Проверочный расчёт тихоходной передачи редуктора по контактным напряжениям
Проверочный расчёт передачи по контактным напряжениям выполняем по формуле:
(3.12)
где 
‑ коэффициент
повышения прочности косозубых передач
по контактным напряжениям;
‑ коэффициент
расчётной нагрузки.
Коэффициент расчётной нагрузки определяем по формуле
=
·
·
(3.13)
Определяем окружную скорость зубчатых колёс по формуле
, (3.14)
м/с
По таблице 8.3, [3]
выбираем коэффициент динамической
нагрузки
=1,02.
Определяем коэффициент расчётной нагрузки:
Коэффициент
определяем по формуле
(3.15)
где 
‑ коэффициент
торцового перекрытия
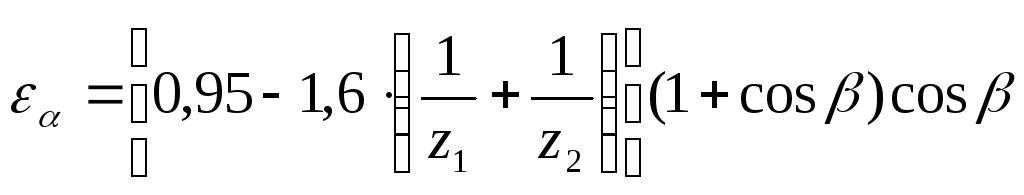(3.16)
Тогда
Определяем контактные напряжения:
МПа
Сравниваем действительные контактные напряжения с допускаемыми:
=
МПа < 
МПа
Недогрузка составляет:
,
Недогрузка передачи составляет более 5%, следовательно, корректируем ширину шестерни по формуле.
, (3.17)
мм
Назначаем ширину
шестерни
мм
Определяем контактные напряжения:
МПа
Сравниваем действительные контактные напряжения с допускаемыми:
=
МПа < 
МПа
Недогрузка составляет:
,
Недогрузка передачи
составляет менее 5%, следовательно,
оставляем расчётное значение ширины
шестерни
мм
3.2.2 Проверочный расчёт тихоходной передачи по напряжениям изгиба
Проверочный расчёт передачи по напряжениям изгиба выполняем по формуле:
(3.18)
где 
‑ коэффициент
повышения прочности косозубых передач
по напряжениям изгиба.
Определяем эквивалентное число зубьев
(3.19)
Для шестерни
Для колеса
По рисунку 8.20, [3] при коэффициенте смещения x = 0:
для шестерни при
числе зубьев
;
для колеса при
числе зубьев
;
Для колеса и для
шестерни находим отношение
Для шестерни
Для колеса
Дальнейший расчёт ведем по наименьшему значению, т.е по колесу.
По рекомендациям
стр. 133, [3] в расчётах принимается
=
,
и в нашем случае
= 1,18.
По графикам на
рисунке 8.15, [3] при
выбираем
= 1,17.
По таблице 8.3, [3]
при степени точности колес – 8,
твердости поверхности зубьев 270 HB
и окружной
скорости
м/с
выбираем
= 1,04
Тогда коэффициент расчётной нагрузки:
.
Коэффициент
определяем по формуле
(3.20)
где 
‑ коэффициент
повышения изгибной прочности вследствие
наклона контактной линии к основанию
зуба.
(3.21)
Тогда
Окружное усилие
на шестерне
,
Н определяем по формуле
(3.22)
Н
Напряжения изгиба в передаче
МПа
280 МПа
Условие изгибной прочности соблюдается.
Определяем радиальное усилие в зацеплении по формуле
(3.23)
Н
Определяем осевое усилие в зацеплении по формуле
(3.24)
Н