Л екция 3

   Электрмагниттік өріс үшін толқындық теңдеу Толқындық теңдеу. Электромагниттік ұйытқудың таралу жылдамдығы. Электромагниттік еркіндік қасиеттері. Электромагниттңк энергияның ағынының тығыздығы. Умов-Пойнтинг векторы

Тербелмелі контур. Еркін, өшетін және еріксіз электромагниттік тербелістер. Айнымалы ток. Айнымалы ток үшін Ом заңы. Кернеулер және тоқтар резонансы.

   Тізбектелген тербелмелі контур ең қарапайым резонансты (тербелмелі) тізбек болып келеді. Ол тізбектей жалғанған катушка және конденсатордан. Мұндай тәзбекке айнымалы (гармоникалық) кернеу әсер еткенде, катушка және конденсатор арқылы шамасы Ом заңына бағынатын: I = U / Х_Σ  айнымалы тоқ өтеді, мұнда Х_Σ – тізбектей жалғанған катушка және конденсатордың реактивті кедергілері (қосынды модулә пайдаланылады).

Ом заңы бойынша контур үшін

мұнда IR – резистордағы кернеу

конденсатордағы кернеу

- айнымалы тоқ жүрген кездегі катушкада пайда болатын өздік индукция э.қ.к.

Сонда

I = q´ , екенін ескеіп және L ға бөліп контурда q зарядының тербелісінің дифференциалды теңдеуін аламыз

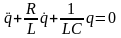- Электромагнитті тербелістердің дифференциалды теңдеуі

Кедергі 0 тең болған кезде, электромагнитті тербелістер гармоническалық болады.

Срнда - Еркін гармоникалық тербелістердің дифференциалды теңдеуі

q заряд гармоникалық тербелісті

_{заңдылығы бойынша жасайды}

мұнда q_m - тербеліс амплитудасы

Тербелмелі контурдағы тоқ

мұнда –тоқ амплитудасы .

Конденсатордағы кернеу

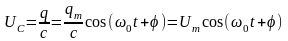
мқнда - кернеу амплитудасы .

Сонымен, I тоқтың тербелісі а qзаряд тербелісін фаза бойынша π/2 ге озып кетеді, яғни т.е. тоқ максимал мәнге жеткенде, заряд q нөлге тең болады және керісінше.

Контурдағы еркін өшпелі тербелістердің дифференциалды теңдеуі:

- өшу коэффициенті және екенін ескерек

Сонда механичекалық тербелістер сияқты, заряд тербелісі төмендегі заңдылыққа бағынады

- еркін өшетін тербелістің кинематикалық теңдеуі

жиілігі

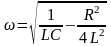
R = 0 болғанда

Логарифмдік өшу декременті

Ne – амплитуданың е есе азайғанға кеткен уақыттағы тербелістер саны.

τ –релаксация уақыты – амплитуданың е есе азайғанға кеткен уақыты

Айнымалы тоқ – шамасы және бағыты жағынан периодты өзгеріп отыратын тоқ.

Ең көп таралған синусоидты айнымилы тоқ, онық лездік мәндері уақыт бойынша синус немесе косинус заңы бойынша өзгереді

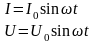
U₀ және I₀ – кернеудің және тоқтың максимал (амплитудалық) мәндері,

ωt – тоқтың фазасы, ω = 2πν – айнымалы кернеудің және тоқтың циклдық жиілігі

Әрқайсына айнымалы кернеу түсірілген тізбектерді қарастырайық U = U_m cos ωt

R L с

~ ~ ~

R кедергі тізбекте активті, себебіол арқылы тоқ өткен кезде қайтымсыз электр энергиясы шығындалады, ол энергияның ьасқа түрлеріне айналады.

- активті кедергі

Резисторы бар тізбекте тоқ күші келсі заң бойынша өзгереді

Кернеу мен тоқ фаза бойынша сәйкес келеді (1 диаграмма )

диаграмма 1	диаграмма 2	диаграмма3

Тоқ катушкасы бар тізбекте фаза бойынша түсірілген кернеуден  /2 шамасына кешігіп отырады 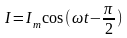(2 диаграмма )

Тоқ конденсаторы бар тізбектегі фаза бойынша түсірілген кернеуден  /2 шамасына озып отырады (2 диаграмма )

катушкасы бар тізбекте

R_L = ωL – индуктивті кедергі

конденсаторы бар тізбекте

- сиымдылықтық кедергі

R_L – R_c – реактивті кедергілер – электр тізбек элементтері қызбайды, яғни электр энергиясы басқа энергия түрлеріне ауыспайды.

Егер тізбектей R_А актив және R_L мен R_c реактивті кедергілер жалғанса онда айнымалы тоқтың толық кедергісі Z келесі формуламен анықталады:

- реактивті кедергі

_{Мұнда жалпы кернеу}U_R, U_L, U_c кернеулердің векторлық қосындысына тең болады (диаграмма 4).

Тоқ пен кернеу фаза бойынша φ бұрышына ығысп тұр.

4диаграммадан осы φ бұрыштың тангенсін анықтайық

Еріксізэлектромагниттік тербелістер – сыртқы периодты түрде өзгеріп отыратын э.қ.к күштің салдарынан тербелістер.

Еріксізэлектромагниттік тербелістердің дифференциалды теңдеуі

- өшу коэффициенті және екенін ескерек

 Реактивті кедергілер әсер етіп отырған айнымалы тоққа калай тәелді екенің еске түсірейік. Катушка үшін бқл тәуелділік келесә түрде болады:

      Формуладан көрініп отырғандай, жиілік жоғарлаған сайын, катушканң реактивті кедергісі жоғарлайды. Конденсатор үшін тәуелдәләк келесә түрде болады:

      Индуктивтілікпен салыстырғанда, конденсаторда керсінше – жиілік жоғарлаған сайын, реактивті кедергі азаяды. 6 суретте катушканың X_L   және конденсатордың Х_C реактивті кедергілерінің ω циклдық (айналмалы) жиіліктен тәуелділіктері графикалық түрде, сонымен қатар, олардың  Х_Σ алгебралық қосындысының   ω жиіліктен тәуелділік графигі келтірілген. Сонда график тізбектей тербелмелі контурдың жалпы реактивті кедергісінің жиіліктен тәуелділігін көрсетеді. 

     

Резонанс – қоздырушы күш жиілігі мен еріксіз тербелістің жиіліктері сәйкес келгенде еріксіз тербелістің амплитудасының күрт өсуі.

Сонымен қатар графиктен көрініп отырғандай, резонанс жиілігінен төменгі жиіліктерде тізбектей тербелмелі контурдың реактивті кедергісі сиымдылықты? ал жоғарғы жиіліктерде - индуктивті. Ең резонансты жиілік Томсон формуласынан қортылады:

Суретте  , U амплитудасы бар идеал генераторға жалғанған R шығыны ескерилген тербелмелі контур келтірілген. Толық кедергі (импеданс): Z = √(R²+X_Σ²), где X_Σ = ω L-1/ωC. Резонанстық жиілікте, катушканың X_L = ωL және конденсатордың Х_С= 1/ωС  реактивты кедергілері модуль жағынан тең болған кезде, X_Σ мәні нолге айналып, тізбек кедергісі тек активті болады, ал тізбектегі тоқ I= U/R қатынасымен анықталады. Бұл жағдайда кернеулер өзара тең болады

 U_L = U_С = IX_L = IX_С.

       Басқа жиіліктерде - олар тоқ амплитудасымен және X_L және X_С реактивті кедергілердің модульдер санымен анықталады. Сондықтан да тізбектей тербелмелі контурдың резонансын кернеулер резонансы деп аталады.

Контурдың резонанстық жиілігі дегеніміз контурдың кедергісі таза активті (резистивті) характер.

Контурдың резонанстық жиілігі деп контурдың кедергісі таза активті (резистивті) болғандағы жиілікті айтамыз.

Резонанстың шарты - катушканың индуктивтілігінің және сиымдылықтың реактивті кедергілерінің мәндерінің теңдігі.

    Резонанстық жиіліктен басқа тербелмелі  контурдың маңызды параметрлерінің бірі болып оның сипаттамалық (немесе толқындық) кедергі ρ және контур сапалығы Q болып табылады. Сипаттамалық (немесе толқындық) кедергі ρ деп резонанстық жиіліктегі кедергіні айтамыз: ρ = Х_L = Х_C (ω =ω_р болғанда).

 ρ = √(L/C).

Сипаттамалық кедергі ρ контурдың реактивті элементтерінің қорларындағы W_L = (LI²)/2  және  W_C=(CU²)/2 энергияларының сандық өлшемі болып келеді. Период аралығындағы контурдың реактивті элементтерінің қорларындағы энергиялардың омдық (резистивті) шығын энергиясына қатынасын контурдың сапалығы Q деп атаймыз.

Тербелмелі контурдың сапалығы - резонанстың амплитудалық-жиіліктік сипаттаманың амплитудасы мен енін сипаттайтын және тербеліс периоды аралығында энергия шығынынан энергия қорының қанша есе көп екенін көрсететін шама. Сапалық R активті кедергінің бар екенін көрсетеді.

       RLC тізбектегі тербелмелі контурдың сапалығы:

Сапалыққа кері шаманы  d = 1 / Q контурдың өшуі деп атайды.

 Q = ρ / R,

мұнда R - резитивті актив шығындарының қуатын сипаттайтын омдық шығындардың кедергісі,  Р = I²R.

Нақты тербелмелі контурлардың сапалығы бірнеше бірліктен жүздікке дейін болады.