6. Определение навигационных элементов счетом в уме

и с использованием микрокалькулятора.

6.1. Решение навигационного треугольника скоростей.

6.1.1. Рассчитываем угол ветра (УВ);

УВ^о = d + 180^о – ЗМПУ – ΔМ

6.1.2. Определяем значение угла сноса (УСр);

УСр^о = U ´ sin УВ^о ´ (60 / Vи)

6.1.3. Определяем значение путевой скорости (Wр);

Wр = U ´ cos УВ^о + Vи (км/ч)

6.1.4. Определяем расчетное время полета ( t р );

t р = S / W ´ 60 (мин)

6.1.5. Рассчитываем магнитный курс (МКр);

МКр = ЗМПУ - УСр

Примеры расчетов.

1. Дано: Решение:

d = 90^о 1. УВ^о = d + 180^о – ЗМПУ – ΔМ = 90 + 180 – 210 – 10 = 50^о

U = 36 км/ч.

ЗМПУ = 210^о 2. УСр^о = U ´ sin УВ^о ´ 60 / Vи = sin 50 ´ 36 ´ 60 / 230 = + 7^о

ΔМ = + 10^о

Vи = 230 км/ч. 3. Wр = U ´ cos УВ^о + Vи = cos 50 ´ 36 + 230 = 253 км/ч.

S = 97 км.

4. t р = S ´ 60 / W = 97 ´ 60 / 253 = 23 мин.

МКр = ЗМПУ - Уср = 210 – 7 = 203^о

2. Дано: Решение:

d = 150^о 1. УВ^о = d + 180^о – ЗМПУ – ΔМ = 150 + 180 – 110 – (-8) = 228^о

U = 40 км/ч.

ЗМПУ = 110^о 2. УСр^о = U ´ sin УВ^о ´ 60 / Vи = sin 228 ´ 40 ´ 60 / 220 = - 8^о

ΔМ = - 8^о

Vи = 220 км/ч. 3. Wр = U ´ cos УВ^о + Vи = cos 228 ´ 40 + 220 = 193 км/ч.

S = 86 км.

4. t р = S ´ 60 / W = 86 ´ 60 / 193 = 27 мин.

5. МКр = ЗМПУ - УСр = 110 – ( - 8 ) = 118^о

Решение навигационного треугольника скоростей счетом в уме.

В основу решения навигационного треугольника счетом в уме, положено разложение вектора навигационного направления ветра (U) на боковую (Uбок) и (Uэкв) - попутную, или встречную составляющую, в зависимости от направления ветра.

Uбок = U sin a^о. (2.1)

Uэкв = U cos a^о. ( 2.2)

U

Uбок

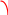a^о U экв лзп

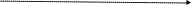
Рис.1

Угол a^о – это угол между линией заданного пути (ЛЗП) и вектором

навигационного направления ветра (U). Измеряется от 0^о до 90^о.

Для определения a^о необходимо вычислить угол ветра (УВ) по формуле:

УВ = dн – ЗМПУ (2.3)

где: ЗМПУ – заданный магнитный путевой угол;

dн – навигационное направление ветра.

Примечание: По значению угла ветра (УВ) определяется знак угла сноса (УС)

и знак эквивалентного ветра (Uэкв).

0^о УВ

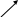УВ от 0^о до 180^о. УС положительный;

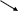90^о УВ от 0^о до 90^о Uэкв – попутный (+).

УВ УВ от 90^о до 180^о Uэкв – встречный (-).

180^о

УВ 0^о (360) УВ от 180^о до 360^о. УС отрицательный;

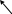УВ от 180^о до 270^о Uэкв – встречный (-).

2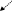 70^о 90^о УВ от 270^о до 360^о Uэкв – попутный (+).

УВ

180^о

Для определения угла a воспользуемся пояснительным рисунком. (рис. 2)

УВ = 0^о(360)

УВ УВ 1 четверть (УВ от 0^о до 90^о) a = УВ

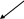
2 четверть (УВ от 90^о до 180^о) a = 180^о - УВ УВ = 90^о

2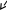 70^о 3 четверть (УВ от 180^о до 270^о) a = УВ - 180^о

4 четверть (УВ от 270^о до 360^о) a = 360^о - УВ

УВ УВ

УВ = 180^о

Рис. 2.

Определив угол a, рассчитываем боковую составляющую вектора ветра (Uбок) и эквивалентный ветер (Uэкв) с использованием таблицы округленных значений тригонометрических функций угла a.

Таблица 1.

aо	0	10	20	30	40	50	60	70	80	90
sin aо	0	0,17	0,34	0,5	0,64	0,76	0,86	0,94	0,98	1
cos aо	1	0,98	0,94	0,86	0,76	0,64	0,5	0,34	0,17	0

Uбок = U ´ sin a^о.

Uэкв = U ´ cos a^о.

Примечание. Значения тригонометрических функций углов a, не указанных

в таблице, определяем методом интерполяции.

Пример: a^о = 15^о sin a^о = 0,3; cos a^о = 0,96.

a^о = 45^о sin a^о = 0,7; cos a^о = 0,7. и т.д.

По значению боковой составляющей (Uбок) вычисляем значение угла сноса расчетного (УСр). Так, как боковая составляющая вектора ветра направлена под углом 90^о к ЛЗП, воспользуемся упрощенной формулой определения УС:

УСр = Uбок ´ 60 / Vи где: Vи - воздушная истинная скорость.

Заменив выражение Vи / 60 коэффициентом К, получим:

УСр = Uбок / К. (2.4)

Значения коэф-та К, для различных скоростей полета,

приведены в табл. 2.

Таблица 2.

Vи км/ч	180	200	220	240
К	3	3,3	3,7	4

С учетом данных таблицы 2 упрощенные формулы

расчета углов сноса примут вид:

Диапазон скоростей: Формулы для расчета:

1. Vи = 175 ÷ 185 км/ч. УСр = Uбок / 3 (2.5)

2. Vи = 190 ÷ 210 км/ч. УСр = (Uбок / 3) - 1^о (2.6)

3. Vи = 215 ÷ 225 км/ч. УСр = (Uбок / 4) + 1^о (2.7)

4. Vи = 230 ÷ 245 км/ч. УСр = Uбок / 4 (2.8)

Для расчета путевой скорости используем формулу:

(2.9) Wр = Vи + ( ± Uэкв)

Примеры расчетов.

1. Дано: Решение:

d = 90^о - Определяем dн - навигационное направление ветра;

U = 36 км/ч. dн = d ± 180^о – (± ΔМ) = 90 +180 – 10 = 260^о

ЗМПУ = 210^о - Рассчитываем значение угла ветра (УВ);

ΔМ = + 10^о УВ = dн – ЗМПУ = 260 – 210 = 50^о a = 50^о

Vи = 230 км/ч. 1 четверть, УС – положительный, Uэкв – положит.

- Определяем значения составляющих:

Uбок = U ´ sin a^о = 36 ´ sin 50^о ≈ 36 ´ 0,75 ≈ 27 км/ч

Uэкв = U ´ cos a^о = 36 ´ cos 50^о = 36 ´ 0,64 ≈ 23 км/ч

Вычисляем значение УСр и Wр:

УСр = Uбок / 4 УСр = Uбок / 4 = 27 / 4 = 6,75 ≈ + 7^о

Wр = Vи + ( ± Uэкв) = 230 + 23 = 253 км/ч. (см.2.9)

2. Дано: Решение:

d = 30^о - Определяем dн - навигационное направление ветра;

U = 40 км/ч. dн = d ± 180^о – (± ΔМ) = 30 +180 + 10 = 220^о

ЗМПУ = 70^о - Рассчитываем значение угла ветра (УВ);

ΔМ = - 10^о УВ = dн – ЗМПУ = 220 – 70 = 150^о a = 30^о

Vи = 180 км/ч. 2 четверть, УС – положительный, Uэкв – отрицат.

- Определяем значения составляющих:

Uбок = U ´ sin a^о = 40 ´ sin 30^о = 40 ´ 0,5 = 20 км/ч

Uэкв = U ´ cos a^о = 40 ´ cos 30^о = 40 ´ 0,86 ≈ 34 км/ч

• Вычисляем значение УСр и Wр:

УСр = Uбок / 3 УСр = Uбок / 3 = 20 / 3 = 6,66 ≈ + 7^о

(см. 2.5) Wр = Vи + ( ± Uэкв) = 180 + 34 = 204 км/ч.

3. Дано: Решение:

d = 180^о

U = 42 км/ч. dн = d ± 180^о – (± ΔМ) = 180 +180 - 5 = 355^о

ЗМПУ = 135^о УВ = dн – ЗМПУ = 355 – 135 = 220^о a = 40^о

ΔМ = + 5^о 3 четверть, УС – отрицательный, Uэкв –отрицат.

Vи = 200 км/ч.

Uбок = U ´ sin a^о = 42 ´ sin 40^о = 42 ´ 0,64 ≈ 27 км/ч Uэкв = U ´ cos a^о = 42 ´ cos 40^о = 42 ´ 0,76 ≈ 32 км/ч

УСр = Uбок / 3 – 1^о УСр = Uбок / 3 – 1^о = 27 / 3 - 1 ≈ - 8^о

(см.2.6) Wр = Vи + ( ± Uэкв) = 200 - 32 = 168 км/ч.

Примечания. 1. При счете в уме, значения тригонометрических функций

угла a^о округляются до десятых. (0.64 ≈ 0,6) и т.д.

2. При определении значения тригонометрических функций

угол a^о можно округлять в пределах ± 5^о. (50^о ≈ 45^о)

С учетом этих примечаний составим таблицу округленных значений

тригонометрических функций для углов a^о. (Только для счета в уме !)

Таблица 3.

aо	0	15	30	45	60	75	90
sin a	0	0,3	0,5	0,7	0,8	0,9	1
cos a	1	0,9	0,8	0,7	0,5	0,3	0

Пример расчетов с использованием табличных данных таблицы 3.

4. Дано: Решение.

d = 170^о dн = d ± 180^о – (± ΔМ) = 170 +180 - 5 = 345^о

U = 40 км/ч. УВ = dн – ЗМПУ = 345 – 110 = 235^о a = 55^о

ЗМПУ = 110^о 3 четверть, УС – отрицательный, Uэкв – отрицат. (см.рис.2)

ΔМ = + 5^о значение a, (55^о) округляем до табличных 60^о

Vи = 185 км/ч. Uбок = U ´ sin a^о = 40 ´ sin 60^о = 40 ´ 0,8 ≈ 32 км/ч

Uэкв = U ´ cos a^о = 40 ´ cos 60^о = 40 ´ 0,5 ≈ 20 км/ч

УСр = Uбок / 3 = 32 / 3 ≈ - 11^о

УСр = Uбок / 3 Wр = Vи + ( ± Uэкв) = 185 - 20 = 165 км/ч.

(см.2.5)

Погрешность в расчетах составляет: по УСр – 0,9^о

Wр – 5км/ч., что вполне допустимо для данных расчетов.

5. Дано: Решение.

d = 220^о dн = d ± 180^о – (± ΔМ) = 220 +180 + 5 = 45^о

U = 36 км/ч. УВ = dн – ЗМПУ = 45 – 10 = 35^о a = 35^о

ЗМПУ = 10^о 1 четверть, УС – положит, Uэкв – положит. (см.рис.2)

ΔМ = - 5^о значение a, (35^о) округляем до табличных 30^о

Vи = 200 км/ч. Uбок = U ´ sin a^о = 36 ´ sin 30^о = 36 ´ 0,5 ≈ 18 км/ч

Uэкв = U ´ cos a^о = 36 ´ cos 30^о = 36 ´ 0,8 ≈ 29 км/ч

УСр = Uбок / 3 – 1^о = 18 / 3 -1 ≈ 5^о

УСр = Uбок / 3 – 1^о Wр = Vи + ( ± Uэкв) = 200 + 29 = 229 км/ч.

(см.2.6)

Погрешность по УС – менее 1^о, по Wр – 1 км/ч.

Определение расчетного времени полета счетом в уме.

Для определения времени полета счетом в уме используется метод

кратности путевой скорости (W) и времени, кратному 1 часу.

W = 200 км/ч --- за 0,5 часа пройденное расстояние составит 100 км.

Коэф-т кратности, в данном случае, равен 1/2.

W = 200 км/ч --- за 20 минут пройденное расстояние составит 67 км.

Коэф-т кратности, в данном случае, равен 1/3.

W = 200 км/ч --- за 15 минут пройденное расстояние составит 50 км.

Коэф-т кратности, в данном случае, равен 1/4.

и т.п.

Примеры расчетов.

1. Дано: Решение.

W = 185 км/ч. Определяем примерную кратность отношения S / W

S = 87 км. 87 / 185. Примерная кратность составит 1 / 2.

t р = ? Расчетное время полета определяем по формуле t р = S / W

С учетом примерной кратности запишем это выражение как;

t р = S / W = 87 / 92,5 ≈ 87 / 93 = (93 - 6) / 93 = 30 – 2 = 28 мин.

Пояснения: С учетом кратности ½, за 30 минут пройденное расстояние

составит 92,5 ≈ 93 км. Расстояние S = 87 км. выразим разностью

(93 - 6). Отсюда имеем; (93 - 6) /93. 93 км за 30 мин. минус 2 мин.

Второе число в числителе (6), в данных расчетах, делим на 3.

2. Дано: Решение.

W = 210 км/ч. Определяем примерную кратность отношения S / W

S = 68 км. 68 / 210. Примерная кратность составит 1 / 3.

t р = ? Расчетное время полета определяем по формуле t р = S / W

С учетом примерной кратности запишем это выражение как;

t р = S / W = 68 / 70 ≈ 68 / 70 = (70 - 2) / 70 = 20 – 1 = 19 мин.

Пояснения: С учетом кратности 1/3 за 20 минут пройденное расстояние

составит 70 км. Расстояние S = 68 км. выразим разностью

(70 - 2). Отсюда имеем; (70 - 2) /70. 70 км за 20 мин. минус 1 мин.

Второе число в числителе (2), в данных расчетах, делим на 3

и округляем до целого числа.

3. Дано: Решение.

W = 168 км/ч. Определяем примерную кратность отношения S / W

S = 96 км. 96 / 168. Примерная кратность составит 1 / 2.

t р = ? Расчетное время полета определяем по формуле t р = S / W

С учетом примерной кратности запишем это выражение как;

t р = S / W = 96 / 84 ≈ (84 + 12) / 84 = 30 + 4 = 34 мин.