Метод расчета индекса рентабельности инвестиций.

Рентабельность инвестиций PI – это показатель, позволяющий определить, в какой мере возрастает ценность фирмы в расчете на 1 руб. инвестиций. Индекс рентабельности является относительным показателем, он характеризует уровень доходов на единицу затрат (формула 17).

Если PI>1, то проект следует принять. Если PI<1, то проект следует отвергнуть. Если PI=1, то проект не является ни прибыльным, ни убыточным.

Метод определения срока окупаемости инвестиций.

Метод состоит в определении того срока, который понадобится для возмещения суммы первоначальных инвестиций. Срок окупаемости – минимальный временной интервал от начала осуществления проекта, с которого затраты покрываются результатами проекта. В оценке инвестиционных проектов критерий срока окупаемости может использоваться двояко: а) проект принимается, если окупаемость имеет место; б) проект принимается только в том случае, если срок окупаемости не превышает установленного на предприятии некоторого лимита.

Метод расчета внутренней нормы прибыли.

Под внутренней нормой прибыли инвестиций IRR (внутренняя доходность, внутренняя окупаемость) понимают значение ставки дисконта r, при котором чистая текущая стоимость проекта равна нулю.

Рассмотрим функцию

где ДП_t – денежный поток в периоде t.

Из вида зависимости видно, что у = f(r) – нелинейная функция. При r = 0 выражение в правой части преобразуется в сумму элементов исходного денежного потока, т.е. график пересекает ось ординат в точке, равной сумме всех элементов недисконтированного денежного потока, включая величину исходных инвестиций (рис.1).

IRR

Рис.1. График NPV классического инвестиционного проекта.

Из формулы видно также, что для проекта, в котором денежные оттоки сменяются притоками, в сумме превосходящими этот отток, соответствующая функция у = f(r) является убывающей, т.е. с ростом r график функции стремится к оси абсцисс и пересекает ее в некоторой точке, как раз и являющейся IRR. Ввиду нелинейности функции, а также возможности различных комбинаций знаков элементов денежного потока, функция может иметь несколько точек пересечения с осью абсцисс.

Смысл расчета внутренней нормы прибыли заключается в следующем: IRR показывает ожидаемую доходность проекта и, следовательно, максимально допустимый относительный уровень расходов, который может быть достигнут в данном проекте. Например, если проект полностью финансируется за счет ссуды банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

Операции наращения и дисконтирования под простые и сложные проценты

Функции (факторы) сложного процента:

1. Б

   (8)

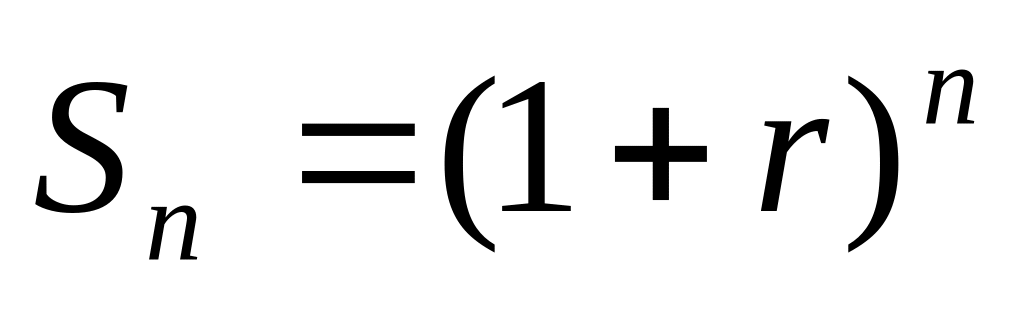   удущая стоимость денежной единицы (накопленная сумма единицы):

где S_n - сумма после n периодов (будущая стоимость денежной единицы);

r – фактическая ставка процента;

n – количество периодов накоплений.

2. Б

   (9)

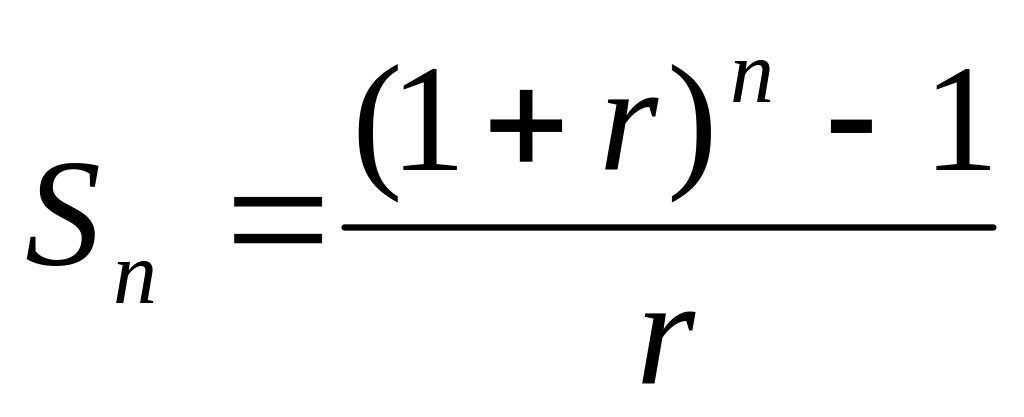   удущая стоимость денежной единицы за период (будущая стоимость аннуитета, накопление единицы за период):

Аннуитет – платежи или поступления денежных средств через одинаковые периоды времени.

3. Ф

   (10)

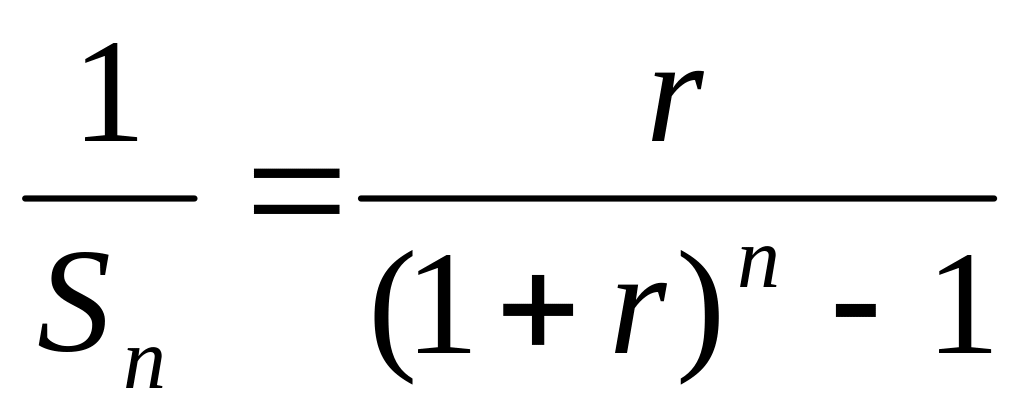   актор фонда возмещения – это величина периодического платежа, которая обеспечивает в течение n периодов при заданной ставке процента накопление суммы капитала равной одной денежной единице.

4. Т

   (11)

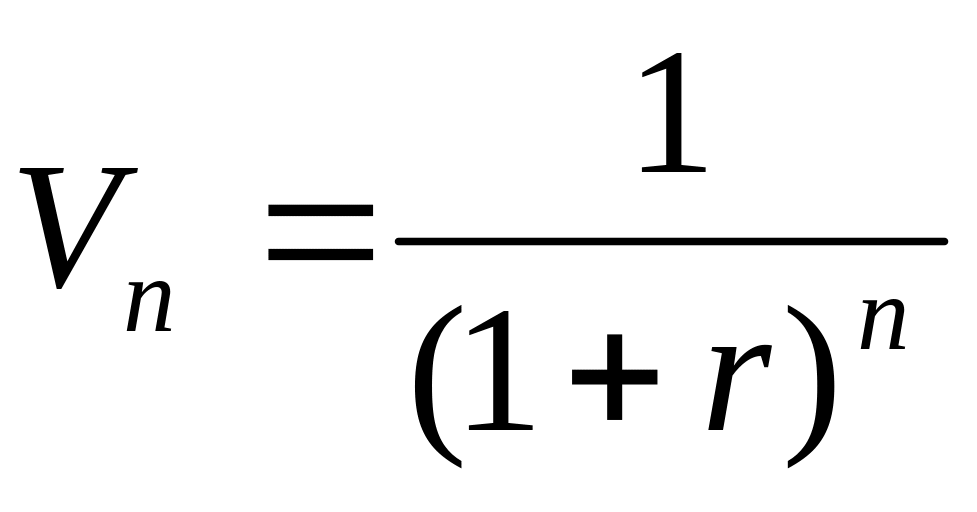   екущая стоимость денежной единицы показывает стоимость на данный момент той единицы, которая будет получена в будущем.

где r – ставка дисконта;

n – количество периодов дисконтирования.

5. Текущая стоимость аннуитета:

(12)

6. В

   (13)

   знос на амортизацию денежной единицы применяется для определения величины платежа при амортизации кредита. Амортизация кредита – погашение долга по кредиту в течение определенного периода времени. За период, в течение которого кредит амортизируется, на остаток суммы кредита начисляются проценты. Необходимо определить, каким по величине должен быть платеж, чтобы серия из n платежей (аннуитет) погашала кредит и накопившиеся по нему проценты. Для того, чтобы аннуитет погашал кредит, текущая стоимость этого аннуитета должна быть равна первоначальной сумме кредита.

г де r – ставка процента по кредиту;

n – срок погашения кредита.

Варианты для решения практических заданий

Задача 1. Кредит выдан сроком до одного года в сумме … тыс.руб. с условием возврата … тыс.руб. (табл.1). Рассчитать процентную и дисконтную ставки.

Таблица 1

Исходные данные по вариантам

Показатели	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Величина кредита, тыс.руб.	200	150	210	250	300	310	260	270	200	230	240	340	380	410	430	450	400	500	370	330
Возвращаемая сумма, тыс.руб.	300	220	280	330	400	390	300	320	260	310	320	400	450	500	520	560	480	590	450	460

Задача 2. Кредит размером в … тыс.руб. выдан на срок … лет под …% годовых (табл.2). Найти полную сумму долга к концу срока, если проценты начисляются: 1) по схеме простых процентов; 2) по схеме сложных процентов.

Таблица 2

Исходные данные по вариантам

Показатели	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Величина кредита, тыс.руб.	30	35	40	33	25	50	55	45	40	35	28	20	34	42	60	55	52	50	44	45
Процентная ставка, %	18	16	20	19	18	20	22	20	18	17	20	18	19	20	20	21	19	18	19	20
Срок погашения кредита, лет	2	3	2	4	3	2	3	4	3	3	2	2	3	3	4	4	3	3	4	3

Задача 3. Сумма в … тыс.руб. помещена в банк на депозит сроком на … лет (табл.3). Ставка по депозиту …%. Проценты по депозиту начисляются раз в квартал по схеме сложных процентов. Какова будет величина депозита в конце срока?

Таблица 3

Исходные данные по вариантам

Показатели	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Сумма, помещенная в банк, тыс.руб.	20	25	40	38	35	30	28	35	25	50	42	40	36	35	28	33	55	30	35	25
Срок вклада, лет	2	3	4	3	4	5	4	5	4	4	3	5	4	3	4	5	4	5	3	5
Ставка по депозиту, %	16	18	20	12	10	8	16	12	16	18	12	10	11	8	10	13	16	12	11	9

Задача 4. Выплаченная по …-летнему депозиту сумма составила … тыс.руб. (табл.4). Определить первоначальную сумму вклада, если ставка по депозиту равна …% годовых (схема сложных процентов).

Таблица 4

Исходные данные по вариантам

Показатели	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Срок депозита, лет	5	6	5	3	4	3	5	6	5	4	3	4	5	6	4	5	3	2	3	4
Выплаченная сумма, тыс.руб.	30	35	32	40	45	41	50	55	43	50	40	38	46	42	35	36	50	52	47	40
Ставка по депозиту, %	18	20	19	17	15	16	18	17	19	14	12	13	11	12	15	14	19	14	10	12

Задача 5. Какая сумма должна быть инвестирована сегодня для получения … тыс.руб. (табл.5) через … лет при начислении процентов по ставке …% годовых (схема сложных процентов): в конце каждого квартала; в конце каждого полугодия; в конце каждого года.

Таблица 5

Исходные данные по вариантам

Показатели	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Накапливаемая сумма, тыс.руб.	100	120	200	250	300	180	140	280	320	400	350	370	330	410	450	260	330	370	440	500
Срок накопления, лет	4	5	4	3	5	4	3	4	5	4	5	4	4	5	5	4	3	3	5	4
Процентная ставка, %	15	16	18	20	17	15	19	18	17	14	20	18	17	18	20	18	16	18	20	17