Механический смысл производной

Пусть при неравномерном прямолинейном движении величина пути, пройденного телом: (t-время)

Пусть

Тогда

Средняя скорость на отрезке

Мгновенная скорость в точке

Мгновенная скорость при неравномерном прямолинейном движении точки характеризует механический смысл производной (от функции пути).

Примеры:

1. Найти значение мгновенной скорости свободно падающего (в пустоте) тела через 3 сек. падения.

( )

Если

2) Для функции найти значение углового коэффициента касательной при x=1.

1 2

x

y

K = =

=

K(1) = 21 = 2 = tg() = arctg2 63⁰.

3) Некоторая популяция микроорганизмов в момент времени t насчитывает

Оценить мгновенную скорость роста популяции через 5 часов развития.



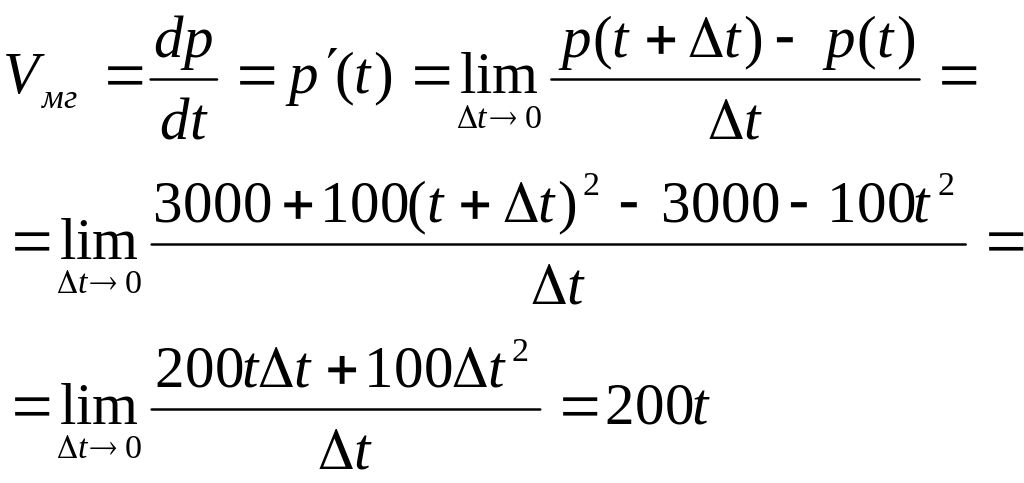
При

Таблица производных основных элементарных функций

№
1	C	0	c, a – const
2		1	u(x), v(x) дифференцируемые функции
3
4
5
6
7	ex	ex
8	ax
9	ln(x)
10
11	Сu(x)	С
12	sin(x)	cos(x)
13	cos(x)	- sin(x)
14	tg(x)
15	ctg(x)
16	arcsin(x)
17	arcos(x)
18	arctg(x)
19	arcctg(x)
20	u(v(x))

Пример. Найти производную функции и вычислить .

Понятие дифференциала функции

В соответствии с определением производной и предела:

( – бесконечно малое при

При но

То есть порядок малости (2) выше, чем порядок малости (1) при .

Выражение - главная часть приращения - называется дифференциалом функции Обозначается .

Так как при

Дифференциал функции равен произведению её производной на дифференциал (или приращение) независимой переменной.

Применение дифференциала (для приближенного вычисления приращения функции)

Задача 1 Оценить, на сколько увеличится объем металлического куба со стороной если при нагревании каждая сторона его увеличилась на 1мм. (

Имеем функцию

Так как мало по сравнению с x, то можно считать

Точное значение: =

Погрешность вычисления