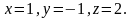- •Волгодонск
- •Порядок выполнения контрольных работ
- •Контрольная работа № 1. Элементы линейной алгебры и аналитической геометрии. Предел и производная функции одной переменной.
- •Библиографический список.
- •Контрольная работа № 2. Приложение производной. Интегралы.
- •Библиографический список.
- •Методические указания к выполнению контрольной работы №1 Матрицы и их приложения
- •Обратные матрицы
- •Элементы векторной алгебры Векторы и линейные операции над ними
- •Элементы аналитической геометрии Уравнения плоскости
- •Уравнения прямой в пространстве
- •Уравнение прямой на плоскости
- •Элементы математического анализа Пределы и непрерывность
- •Производная функции
- •Основные правила дифференцирования
- •Дифференцирование сложной функции
- •Методические указания к выполнению контрольной работы № 2 Приложение производной функции одной переменной
- •Неопределенный интеграл
- •Основные методы интегрирования.
- •1) Подынтегральная функция является произведением многочлена на показательную или тригонометрическую функцию.
- •2) Подынтегральная функция является произведением многочлена на логарифмическую или обратную тригонометрическую функцию.
- •Определенный интеграл и его приложения
Библиографический список.
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Т.1.-M.: Наука, 1985.- 456с.
2. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов - СПб.: Изд-во “Лань”, 2003. – 736c.
Методические указания к выполнению контрольной работы №1 Матрицы и их приложения
Матрицей
размера
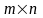 называется прямоугольная таблица чисел
называется прямоугольная таблица чисел
 ,
,
имеющая
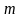 строк (одинаковой длины) и
строк (одинаковой длины) и
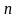 (одинаковой длины) столбцов.
(одинаковой длины) столбцов.
Элементы
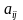 матрицы снабжаются двумя индексами,
первый из которых обозначает номер
строки, второй - номер столбца, на
пересечении которых стоит элемент
.
Если матрица имеет
строк и
столбцов, то матрицу называют квадратной.
матрицы снабжаются двумя индексами,
первый из которых обозначает номер
строки, второй - номер столбца, на
пересечении которых стоит элемент
.
Если матрица имеет
строк и
столбцов, то матрицу называют квадратной.
Матрицы
одинакового размера можно складывать.
При этом суммой матриц
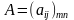 и
и
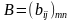 называют матрицу
называют матрицу
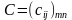 ,
для которой
,
для которой
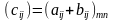 .
.
Например,
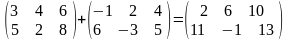 .
.
Произведением
матрицы
на число
 называют матрицу
,
каждый элемент которой
называют матрицу
,
каждый элемент которой
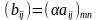 .
Например,
.
Например,
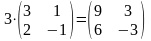 .
.
Задача.
Даны матрицы
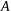 и
и
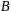 :
:
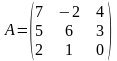 ;
;
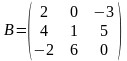 .
.
Найти
матрицы: a)
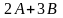 ,
б)
,
б)
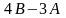 .
.
Решение.
а)
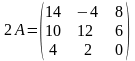 ;
;
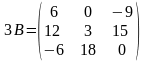 ;
;
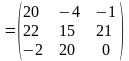 ;
;
б)
 ;
;
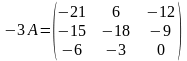 ;
;
 ;
;
Произведением
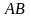 матрицы
матрицы
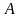 размером
на матрицу
размером
на матрицу
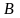 размером
размером
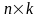 называют матрицу C
размером
называют матрицу C
размером
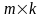 ,
каждый элемент которой
,
каждый элемент которой
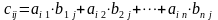 ,
где
,
где
 ;
;
 .
.
То
есть элемент
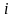 – ой строки и
– ой строки и
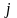 – го столбца матрицы произведения
– го столбца матрицы произведения
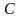 равен сумме произведений элементов
–
ой строки матрицы
на соответствующие элементы
–
го столбца матрицы
.
равен сумме произведений элементов
–
ой строки матрицы
на соответствующие элементы
–
го столбца матрицы
.
Если
определено произведение
,то
это не значит, что определено произведение
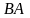 .
Это произведение может не иметь смысла.
Если выполняется
.
Это произведение может не иметь смысла.
Если выполняется
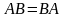 ,
то матрицы называются перестановочными,
или коммутирующими. Отметим сразу же,
что обычно
,
то матрицы называются перестановочными,
или коммутирующими. Отметим сразу же,
что обычно
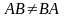 .
.
Задача. Даны матрицы и :
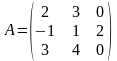 ;
;
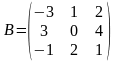 .
.
Найти матрицу .
Решение.
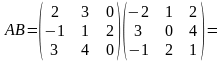
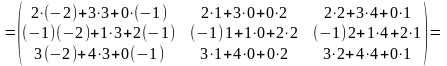
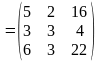 .
.
.
Обратные матрицы
Квадратная
матрица
называется обратимой, если существует
матрица такая, что
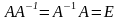 .
Эту матрицу называют обратной к матрице
и
обозначают
.
Эту матрицу называют обратной к матрице
и
обозначают
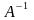 .
.
Каждой
квадратной матрице
соответствует определитель
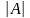 .
Оказывается, что если
.
Оказывается, что если
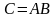 ,
то
,
то
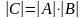 .
Так как
.
Так как
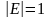 ,
то
,
то
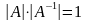 .
.
Необходимым
и достаточным условием существования
обратной матрицы является условие
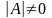 .
.
Алгебраическим
дополнением
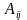 элемента
называется произведение числа
элемента
называется произведение числа
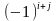 на
определитель, получающийся при
вычеркиванием
-ой
строки и
-го
столбца. Например, определитель
на
определитель, получающийся при
вычеркиванием
-ой
строки и
-го
столбца. Например, определитель
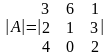
имеет следующие алгебраические дополнения:
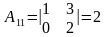 ;
;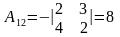 ;
;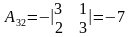 ;
;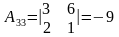 .
.
Если определитель матрицы отличен от нуля , то обратную матрицу строят следующим образом:
1) находят все алгебраические дополнения;
2)
составляют матрицу алгебраических
дополнений
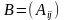 ;
;
3)
транспонируют матрицу B и умножают на
число
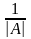 .
.
Полученная матрица и будет обратной матрицей.
Задача. Решить матричным способом систему уравнений

Решение. Положим, что
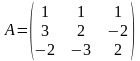 ;
;
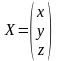 ;
;
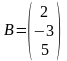 .
.
Тогда матричная запись рассматриваемой системы уравнений будет иметь вид
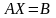 .
(10)
.
(10)
Найдем
определитель
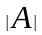 матрицы
:
матрицы
:
 .
.
Так
как
,
то существует обратная матрица
.
Умножая слева на матрицу
равенство (10), получим, что
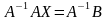 или
или
 .
Найдем обратную матрицу
:
.
Найдем обратную матрицу
:
 ;
;
 ;
;
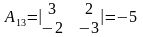 ;
;
 ;
;
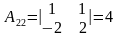 ;
;
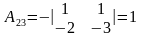 ;
;
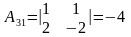 ;
;
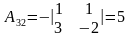 ;
;
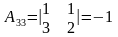 .
.
Обратная
матрица
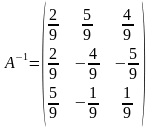 .
.
Но
тогда
 .
.
Ответ: