
- •Волгодонск
- •Порядок выполнения контрольных работ
- •Контрольная работа № 1. Элементы линейной алгебры и аналитической геометрии. Предел и производная функции одной переменной.
- •Библиографический список.
- •Контрольная работа № 2. Приложение производной. Интегралы.
- •Библиографический список.
- •Методические указания к выполнению контрольной работы №1 Матрицы и их приложения
- •Обратные матрицы
- •Элементы векторной алгебры Векторы и линейные операции над ними
- •Элементы аналитической геометрии Уравнения плоскости
- •Уравнения прямой в пространстве
- •Уравнение прямой на плоскости
- •Элементы математического анализа Пределы и непрерывность
- •Производная функции
- •Основные правила дифференцирования
- •Дифференцирование сложной функции
- •Методические указания к выполнению контрольной работы № 2 Приложение производной функции одной переменной
- •Неопределенный интеграл
- •Основные методы интегрирования.
- •1) Подынтегральная функция является произведением многочлена на показательную или тригонометрическую функцию.
- •2) Подынтегральная функция является произведением многочлена на логарифмическую или обратную тригонометрическую функцию.
- •Определенный интеграл и его приложения
Министерство образования и науки
Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Контрольные работы по курсу
«Математика»
для студентов-заочников 1 курса
специальности
«Машиностроение»
и методические указания к их выполнению
Волгодонск
2013
УДК 811.111-36 (076.5)
Рецензент д.т.н., проф. А.В. Чернов
Сысоев Ю.С., Замыслова А.И., Алексеева М.А., Лисичкина О.М., Столяр Л.Н., Чабанова Н.И. Контрольные работы по математике для студентов-заочников 1 курса и методические указания к их выполнению. / Ю.С. Сысоев, А.И. Замыслова, М.А. Алексеева, О.М. Лисичкина, Л.Н. Столяр, Н.И. Чабанова. – Волгодонский инженерно-технический институт (ф) НИЯУ МИФИ.
Данное пособие предназначено для студентов-заочников, выполняющих контрольные работы по курсу «Математика» в соответствии с унифицированными планами, составленными в ВИТИ НИЯУ МИФИ. Сборник охватывает все темы, предусмотренные соответствующими ФГОС.
© ВИТИ НИЯУ МИФИ, 2013
© Коллектив авторов, 2013
Порядок выполнения контрольных работ
Сборник содержит две контрольных работы для студентов-заочников 1 курса всех направлений, по которым ведется обучение в Волгодонском инженерно-техническом институте — филиале НИЯУ МИФИ. Эти контрольные работы охватывают все разделы, представленные в федеральных государственных образовательных стандартах, и составлены в соответствии с унифицированными планами и соответствующими рабочими программами подготовки бакалавров всех направлений филиала.
Предусмотрен следующий порядок выполнения контрольных работ:
Семестр |
I |
II |
Номера контрольных работ |
1 |
2 |
Выбор варианта производится по последней цифре номера зачетной книжки.
Контрольная работа № 1. Элементы линейной алгебры и аналитической геометрии. Предел и производная функции одной переменной.
Задание 1. Дана система линейных уравнений
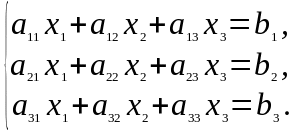
Решить двумя способами: 1) методом Крамера; 2) методом матричного исчисления.
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
Задание 2. Даны
координаты вершин пирамиды
 .
Найти:
.
Найти:
1) длину ребра
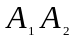 ;
;
2) угол между ребрами
и
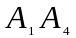 ;
;
3) площадь грани
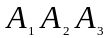 ;
;
4) объем пирамиды ;
5) уравнение прямой ;
6) уравнение плоскости ;
Вариант |
|
|
|
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
|
|
|
7. |
|
|
|
|
8. |
|
|
|
|
9. |
|
|
|
|
10. |
|
|
|
|
Задание 3. Найти пределы функций, не пользуясь правилом Лопиталя.
1. |
а)
в)
|
2. |
а)
в)
|
3. |
а)
|
|
в)
|
4. |
а)
в)
|
5. |
а)
в)
|
6. |
а)
в)
|
7. |
а)
в)
|
8. |
а)
в)
|
9. |
а)
в)
|
10. |
а)
в)
Задание 4. Найти производные данных функций.
1.
а) 2.
а)
3.
а)
4.
а)
5.
а)
6.
а) 7.
а)
8.
а)
9.
а)
10.
а)
|

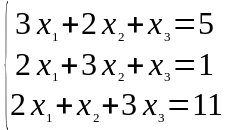
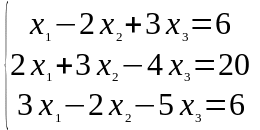
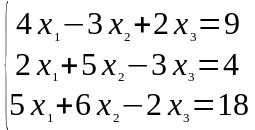
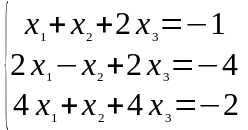
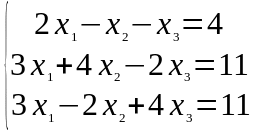
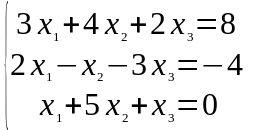
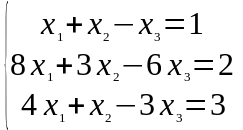
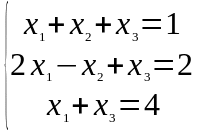
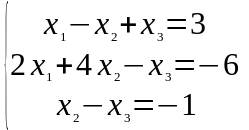


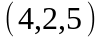
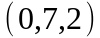
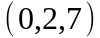

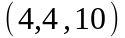
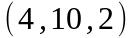
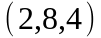
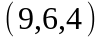
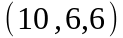
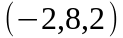
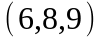
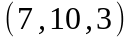
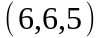
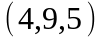
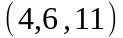
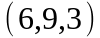
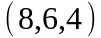
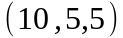
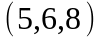
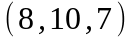
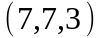
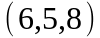
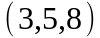
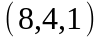
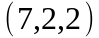
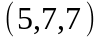

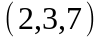
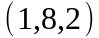
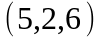

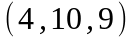

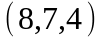
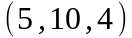
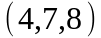
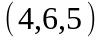
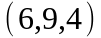
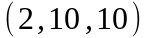

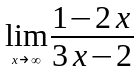 ;
б)
;
б)
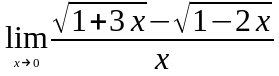 ;
;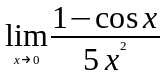 ;
г)
;
г)
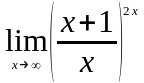 .
.
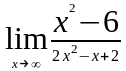 ;
б)
;
б)
 ;
;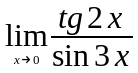 ;
г)
;
г)
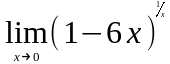 .
.
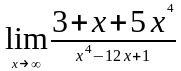 ;
б)
;
б)
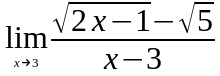 ;
;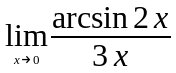 ;
г)
;
г)
 .
.
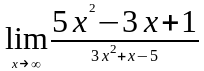 ;
б)
;
б)
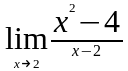 ;
;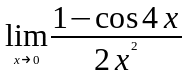 ;
г)
;
г)
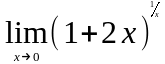 .
.
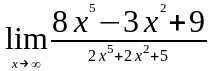 ;
б)
;
б)
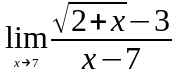 ;
;
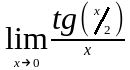 ;
г)
;
г)
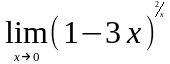 .
.
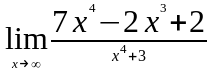 ;
б)
;
б)
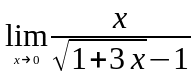 ;
;
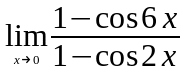 ;
г)
;
г)
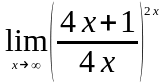 .
.
 ;
б)
;
б)
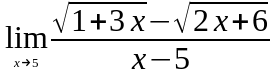 ;
;
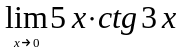 ;
г)
;
г)
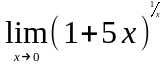 .
.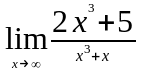 ;
б)
;
б)
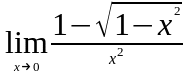 ;
;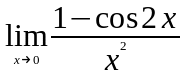 ;
г)
;
г)
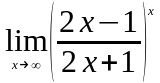 .
.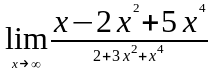 ;
б)
;
б)
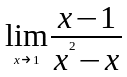 ;
;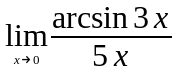 ;
г)
;
г)
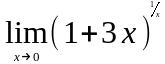 .
. ;
б)
;
б)
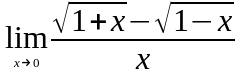 ;
;
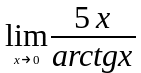 ;
г)
;
г)
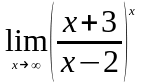 .
.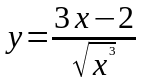 ,
б)
,
б)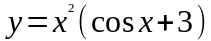 ,
в)
,
в)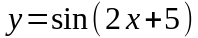 .
.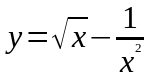 ,
б)
,
б)
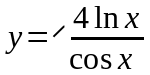 ,
в)
,
в)
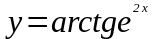 .
.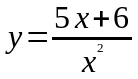 ,
б)
,
б)
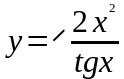 ,
в)
,
в)
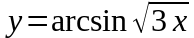 .
.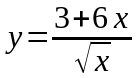 ,
б)
,
б)
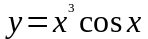 ,
в)
,
в)
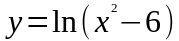 .
. ,
б)
,
б)
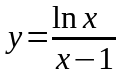 ,
в)
,
в)
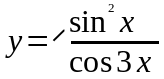 .
.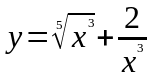 ,
б)
,
б)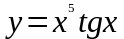 ,
в)
,
в) .
.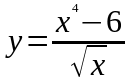 ,
б)
,
б)
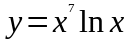 ,
в)
,
в)
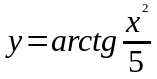 .
. ,
б)
,
б)
 ,
в)
,
в)
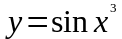 .
.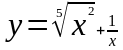 ,
б)
,
б)
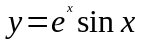 ,
в)
,
в)
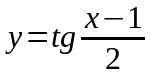 .
.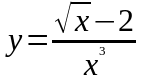 ,
б)
,
б) ,
в)
,
в)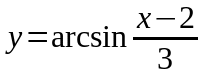 .
.