
- •Методические указания по выполнению практических работ
- •Задания на практическую работу
- •Практическая работа №1
- •Практическая работа №2
- •Практическая работа №3
- •Практическая работа №4
- •Алгоритм нахождения экстремумов функции и интервалов ее монотонности с помощью первой производной
- •Практическая работа №5
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Практическая работа №6
- •Практическая работа №7 Тема: Разложение функций в ряд Фурье.
- •Практическая работа №8
- •Задание: Исследовать на сходимость числовой ряд с помощью признака Коши:
- •1.Признак сравнения
- •2. Признак Даламбера
- •3.Радикальный признак Коши
- •Практическая работа №10
- •Практическая работа №11
- •Практическая работа №12
- •Практическая работа №13
- •Практическая работа №14
- •Практическая работа №15
- •Практическая работа №16
- •Практическая работа №17
- •Практическая работа №18
- •Практическая работа №19
- •Практическая работа №20
- •Образец выполнения работы: Практическая работа №1 Действие над комплексными числами в алгебраической форме
- •Литература:
Алгоритм нахождения экстремумов функции и интервалов ее монотонности с помощью первой производной
1. Найти область определения функции и интервалы, на которых функция непрерывна.
2. Найти производную функции f '(x).
3. Найти критические точки функции y = f (x), т.е. точки, принадлежащие области определения функции, в которых производная f '(x) обращается в нуль или не существует.
4. Исследовать характер изменения функции f (x) и знак производной f '(x) в промежутках, на которые найденные критические точки делят область определения функции y = f (x).
5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.
Помни: критическая точка x0 есть точка минимума, если она отделяет промежуток, в котором f '(x)<0, от промежутка, в котором f '(x)>0, и точка максимума - в противном случае. Если же в соседних промежутках, разделенных критической точкой x0, знак производной не меняется, то в точке x0 функция экстремума не имеет.
6. Вычислить значения функции в точках экстремума.
7. Записать результат исследования функции: промежутки монотонности и экстремумы.
Общая схема исследования функции
Найти область определения функции. Выделить особые точки (точки разрыва).
Установить, является ли функция чётной или нечётной.
Найти точки пересечения с осями координат.
Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается).
Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.
Найти точки перегиба и интервалы выпуклости-вогнутости.
Построить график функции.
Содержание отчета
Титульный лист в соответствии с СТП1.2-2005.
Цель работы
Задание
Выполненная практическая работа в соответствии с заданием
Ответы на контрольные вопросы
Вывод
Контрольные вопросы:
Дайте определение критической точкой функции.
Сформулируйте признак возрастания (убывания) функции.
Сформулируйте признак максимума (минимума) функции.
Дайте определение точки перегиба функции.
Запишите определение точек экстремума функции.
Практическая работа №5
Тема: Вычисление площадей и объемов при проектировании объектов транспорта с применением определенного интеграла.
Цель работы: Корректировать знания, умения и навыки по теме: «Дифференциальное и интегральное исчисление».
Задание: Вычислить площадь фигуры, ограниченной линиями:
1. |
|
4. |
|
2. |
|
5. |
|
3. |
|
6. |
|
Задание: Вычислить площадь фигуры, ограниченной линиями:
7. |
|
10. |
|
8. |
|
11. |
|
9. |
|
12. |
|
Задание: Вычислите площадь фигуры, ограниченной линиями:
13. |
у = -х2 + 8х - 16; у = х2 - 4х. |
16. |
|
14. |
|
17. |
у = х2 - 4х + 6, у = 4х - х2. |
15. |
у = - х2 + 2х + 3; у = х2 - 6х - 7. |
18. |
у = х2 - 2х + 2; у = -х2 + 4х + 2. |
Задание: Вычислить объем тела:
19. |
Полученного
при вращении вокруг оси Ох
криволинейной
трапеции, ограниченной гиперболой
|
22. |
Полученного
при вращении вокруг оси Оy
трапеции,
образованной прямыми
|
20. |
Образованного вращением вокруг оси Оу фигуры, ограниченной кривой
|
23. |
Образованного
вращением вокруг оси Ох
фигуры, ограниченной одной полуволной
синусоиды
|
21. |
Полученного
при вращении вокруг оси Ох
трапеции, образованной прямыми
|
24. |
Полученного
отвращения кривой
|
Задание: Решить задачу:
25. |
Скорость
движения поезда задается формулой
|
28. |
Скорость
движения поезда задается формулой
|
26. |
Найти
путь, пройденный поездом за 10-ю секунду,
зная, что скорость прямолинейного
движения выражается формулой
|
29. |
Скорость движения поезда задается формулой
|
27. |
Найти
путь, пройденный поездом за 4-ю секунду,
зная, что скорость прямолинейного
движения выражается формулой
|
30. |
Скорость
движения изменяется по закону
|
Пояснения к работе:
Необходимые формулы:







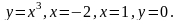
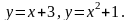


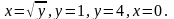



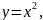

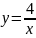 , прямыми
, прямыми
 =12
и осью абсцисс.
=12
и осью абсцисс.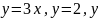 =4
и осью ординат.
=4
и осью ординат.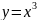 и
отрезком
и
отрезком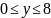 оси
ординат.
оси
ординат. и
отрезком
и
отрезком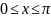 оси
абсцисс.
оси
абсцисс. =6
и осью абсцисс.
=6
и осью абсцисс. вокруг оси Оy
в
пределах от
вокруг оси Оy
в
пределах от
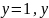 =5.
=5. км/ч.
Найти путь пройденный поездом за
первые 4с от начала движения.
км/ч.
Найти путь пройденный поездом за
первые 4с от начала движения.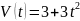 км/ч.
Найти путь пройденный поездом за
первые 4с от начала движения.
км/ч.
Найти путь пройденный поездом за
первые 4с от начала движения. км/ч
км/ч км/ч.
Найти путь пройденный поездом за
первые 4с от начала движения.
км/ч.
Найти путь пройденный поездом за
первые 4с от начала движения. км/ч
км/ч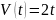 км/ч.
Найти длину пути, пройденного телом
за 3-ю секунду его движения.
км/ч.
Найти длину пути, пройденного телом
за 3-ю секунду его движения.