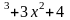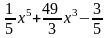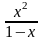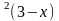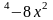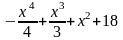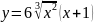Практическая работа №4
Тема: Определение максимума мощности в цепи постоянного тока с применением производной.
Цель работы: Корректировать знания, умения и навыки по теме: «Дифференциальное и интегральное исчисление».
Задание: Выполните задание по чертежу:
1. |
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10]. |
4. |
На рисунке изображен график функции у = f (x) , определенной на интервале (-6; 5). Найдите сумму точек экстремума функции f (x). |
2. |
На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6]. |
5. |
На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x). |
3. |
На рисунке изображен график функции у = f (x), определенной на интервале (-5; 6). Найдите сумму точек экстремума функции f(x). |
6. |
На рисунке изображён график производной функции определенной на интервале (−8; 9). Найдите количество точек минимума у = f (x), функции принадлежащих отрезку [−4; 8]. |
Задание: Выполните задание по чертежу:
7. |
На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. |
10. |
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них. |
8. |
На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
|
11. |
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
|
9. |
На
рисунке изображён график производной
функции
|
12. |
На рисунке изображён график производной функции и восемь точек на оси абсцисс: x1, x2, x3,…, x8. В ответе укажите точки, в которых функция возрастает. |
и
восемь точек на оси абсцисс:
x1,
x2,
x3,…,
x8.
В ответе
укажите точки, в которых функция
убывает.
Задание: Найти точки экстремума и определить их характер:
13. |
y=x
|
16. |
y=- |
14. |
y= |
17. |
y=(x+1) |
15. |
y=x
|
18. |
y= |
Задание: Исследуйте на экстремум функцию:
19. |
|
22. |
|
20. |
|
23. |
|
21. |
|
24. |
|
Задание: Постройте график функции:
25. |
|
28. |
|
26. |
|
29. |
|
27. |
|
30. |
|
Пояснения к работе:
Необходимые формулы: