- •Методические указания по выполнению практических работ
- •Задания на практическую работу
- •Практическая работа №1
- •Практическая работа №2
- •Практическая работа №3
- •Практическая работа №4
- •Алгоритм нахождения экстремумов функции и интервалов ее монотонности с помощью первой производной
- •Практическая работа №5
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Практическая работа №6
- •Практическая работа №7 Тема: Разложение функций в ряд Фурье.
- •Практическая работа №8
- •Задание: Исследовать на сходимость числовой ряд с помощью признака Коши:
- •1.Признак сравнения
- •2. Признак Даламбера
- •3.Радикальный признак Коши
- •Практическая работа №10
- •Практическая работа №11
- •Практическая работа №12
- •Практическая работа №13
- •Практическая работа №14
- •Практическая работа №15
- •Практическая работа №16
- •Практическая работа №17
- •Практическая работа №18
- •Практическая работа №19
- •Практическая работа №20
- •Образец выполнения работы: Практическая работа №1 Действие над комплексными числами в алгебраической форме
- •Литература:
Практическая работа №2
Тема: Вычисление простейших определенных интегралов.
Цель работы: Корректировать знания, умения и навыки по теме: «Дифференциальное и интегральное исчисление».
Задание: Вычислить определенный интеграл
1. |
|
4. |
|
2. |
|
5. |
|
3. |
|
6. |
|
Задание: Вычислить определенный интеграл:
7. |
|
10. |
|
8. |
|
11. |
|
9. |
|
12. |
|
Задание: Вычислить определенный интеграл методом непосредственного интегрирования:
13. |
|
16. |
|
14. |
|
17. |
|
15. |
|
18. |
|
Задание: Вычислить интеграл способом подстановки (замены переменной):
19. |
|
22. |
|
20. |
|
23. |
|
21. |
|
24. |
|
Задание: Вычислить интеграл методом интегрирования по частям:
25. |
|
28. |
|
26. |
|
29. |
|
27. |
|
30. |
|
Пояснения к работе:
Необходимые формулы:
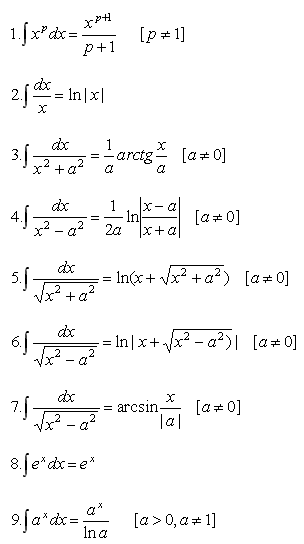
Интегрирование
произведения (функции) на постоянную: ![]()
Интегрирование суммы функций:
![]()
Формула
интегрирования по частям неопределенные
интегралы:
![]()
Формула интегрирования по частям определенные интегралы:

Формула Ньютона-Лейбница определенные интегралы:

Где F(a),F(b)-значения первообразных в точках b и a соответственно.
Содержание отчета
Титульный лист в соответствии с СТП1.2-2005.
Цель работы
Задание
Выполненная практическая работа в соответствии с заданием
Ответы на контрольные вопросы
Вывод
Контрольные вопросы:
Дайте определение первообразной функции.
Дайте определение определенного интеграла.
Запишите формулу Ньютона-Лейбница.
Запишите геометрический смысл определенного интеграла.
Запишите основные формулы интегрирования.
Практическая работа №3
Тема: Расчет сопряжений с применением производной в инженерной графике.
Цель работы: Корректировать знания, умения и навыки по теме: «Дифференциальное и интегральное исчисление».
Задание: Решить задачу на физический смысл производной:
1. |
Материальная
точка движется прямолинейно
по закону |
4. |
Материальная
точка движется прямолинейно
по закону |
2. |
Материальная
точка движется прямолинейно
по закону |
5. |
Материальная
точка движется прямолинейно
по закону |
3. |
Материальная
точка движется прямолинейно
по закону |
6. |
Материальная
точка движется прямолинейно
по закону |
Задание: Решить задачу на геометрический смысл производной:
7. |
Прямая |
10. |
Прямая |
8. |
Прямая |
11. |
Прямая |
9. |
Прямая |
12. |
Прямая |
Задание: Найдите тангенс угла наклона касательной, проведенной к графику функции:
13. |
у
= 6х- |
16. |
|
14. |
у = 4-х2 в его точке с абсциссой равной -6. |
17. |
f(x)=(x−6)(x2+6x+36) в его точке с абсциссой равной 1. |
15. |
у
= -
|
18. |
|
Задание: На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.:
19. |
|
22. |
|
20. |
|
23. |
|
21. |
|
24. |
|
Задание: Найдите наибольшее и наименьшее значения функции на промежутке:
25. |
f (x) = x3 – 3x2 + 3x + 2; [– 2; 2]
|
28. |
f (x) = 9 – 6x2 – x3 [– 4; 2];
|
26. |
y = 9x + 3x2 – x3 ; [– 2; 2]
|
29. |
y = 4 – 9х + 3x2 + x3 [– 2; 2]
|
27. |
y = 5 + x4 – 8x [– 3 ; 2]
|
30. |
f(х) =2х3 + 3х2 – 36х [– 4; 3] |
Пояснения к работе:
Необходимые формулы:
Геометрический смысл производной:
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.

Уравнение касательной к графику функции y=f(x) в точке x0 :
![]()
Физический смысл производной:
Если
точка движется вдоль оси х и ее координата
изменяется по закону x(t), то мгновенная
скорость точки:
![]()
Алгоритм нахождения наибольшего (наименьшего) значения функции:
1.Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции: Если на промежутке производная функции >0, то функция возрастает на этом промежутке. Если на промежутке производная функции <0, то функция убывает на этом промежутке.
5. Находим точки максимума и минимума функции. В точке максимума функции производная меняет знак с "+" на "-". В точке минимума функции производная меняет знак с "-" на "+".
6. Находим значение функции в концах отрезка, затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции.
Содержание отчета
Титульный лист в соответствии с СТП1.2-2005.
Цель работы
Задание
Выполненная практическая работа в соответствии с заданием
Ответы на контрольные вопросы
Вывод
Контрольные вопросы:
Запишите алгоритм исследования графика функции.
Дайте определение касательной к графику функции.
Сформулируйте алгоритм составления уравнения касательной к графику функции.
Запишите алгоритм исследования непрерывной функции на монотонность и экстремумы.
Запишите алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке [a; в].




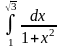

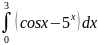

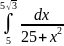
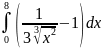
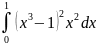
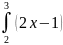 3
dx
3
dx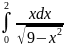
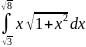
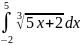
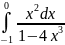

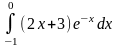
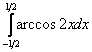
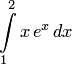
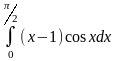
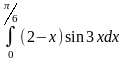
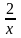 в его точке с абсциссой равной -1.
в его точке с абсциссой равной -1.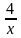 в его
точке с абсциссой равной -2.
в его
точке с абсциссой равной -2.