Змістовний модуль 2 Елементи математичної статистики

Тема 2.1. Елементи комбінаторики.

2.1.1.Основні поняття комбінаторики

Комбінаторика - розділ математики, у якому вивчаються питання про підрахунок різних комбінацій (вибірок), залежних від тих чи інших умов, які можна скласти з елементів заданій множині.

Основна теорема комбінаторики. Якщо деякий складний експеримент складається з двох простих експериментів, що мають n і m наслідків, то складний експеримент має nm наслідків.

Приклад . Скільки трицифрових чисел можна утворити в десятковій системі числення?

Рішення.

На місце одиниць і десятків трицифрового числа можна записати кожну з десяти цифр: 0,1,2,3,4,5,6,7,8,9, тобто число десятків і число одиниць можна записати десятьма способами, а на місце сотень можна записати будь-яке число, крім нуля, тобто число сотень можна записати дев'ятьма способами. Таким чином, з основної теореми комбінаторики випливає, що кількість трицифрових чисел дорівнює

.

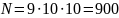Генеральна сукупність без повторень обсягу n – це набір деякого кінцевого числа різних елементів: а₁, а₂, …а_n…

Вибірка обсягу m 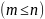- це довільна група з m елементів даної генеральної сукупності.

2. Комбінації елементів, перестановки, розміщення.

Числом розміщень з n елементів по m називається кількість способів, якими можна розташувати у визначеному порядку m елементів з n. Визначається формулою:

,

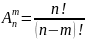де n!=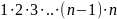 . Причому, за означенням, прийнято вважати 0!=1.

Приклад . У кружку юних математиків, що складається з 25 чоловік, необхідно обрати голову кружка, його заступника, редактора стінної газети і секретаря. Скількома способами можна утворити керівну четвірку, якщо один учень може займати тільки одну посаду?

Рішення.

Керівники четвірки можуть відрізнятися складом членів і посадою, яку обіймають. Тобто елементи вибірки будуть відрізнятися складом членів і порядком їхнього розміщення. Отже, задачу можна вирішити, застосувавши формулу числа розміщень з 25 по 4.

.

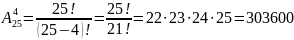Числом перестановок з n елементів називається кількість способів, якими можна розташувати n елементів у визначеному порядку. Число переставлень з n елементів визначається формулою

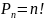
Приклад . Якою кількістю способів можна розмістити 6 студентів у чергу за стипендією?

Рішення.

Вибірки з 6 чоловік будуть відрізнятися тільки порядком розміщення елементів, тобто необхідно знайти число перестановок з 6 елементів.

.

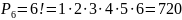Числом сполучень з n елементів по m називається кількість способів, якими можна вибрати m елементів з n. Число сполучень з n елементів по m визначається формулою

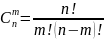
Приклад. На тренуваннях займаються 12 баскетболістів. Скільки різних стартових п'ятірок може утворити тренер?

Рішення.

При утворенні стартової п'ятірки тренера цікавить тільки ї склад, тому досить визначити число сполучень з 12 по 5.

.

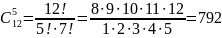Тема 2.2 . Елементи теорії ймовірностей

1. Ймовірність випадкової події

Ймовірність – це деяка функція, яка визначена на ймовірнісному просторі і приймає значення на відрізку .

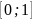Визначення. Ймовірністю події А називається відношення числа результатів випробування, сприятливих події а, до числа всіх рівно можливих і попарно несумісних результатів випробування.

.

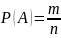Приклад. У партії з 10 деталей 7 стандартних. Знайти імовірність того, що серед шести узятих навмання деталей 4 стандартних.

Рішення. У партії 10 деталей: 7 стандартних і 3 нестандартні. Подія А – з партії витягнули 6 деталей: 4 стандартні і 2 нестандартні.

Загальне число елементарних наслідків іспиту дорівнює числу сполучень з 10 елементів по 6 елемента, тобто 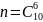. Чотири стандартні деталі можна взяти із 7 стандартних деталей 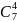способами, а дві нестандартні - 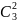. Отже число сприяючих наслідків дорівнює .

Ймовірність дорівнює

.
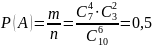