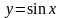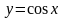- •Змістовний модуль 1 Функції та обчислення
- •Тема 1.1 Функції, обчислення, властивості та графіки
- •1.1.1Визначення та властивості функції.
- •1.1.2. Область визначення функції.
- •1.1.3. Способи завдання функції.
- •1.1.4. Парність та непарністьь.
- •4. Область визначення функції
- •1.1.5. Періодичність.
- •1.1.6. Монотонність .
- •1.1.7. Обмежені функції.
- •1.1.8. Перетворення графіків функцій.
- •1.1.9. Основні елементарні функції.
- •Тема 1.2. Границі функції. Неперервність функції
- •1.2.1. Границя функції f(X) якщо х стримиться до хо(х → хо).
- •1.2.2. Ліва та права границя функції .
- •1.2.3. Границя функції при X→ ∞.
- •1.2.4. Правила граничного переходу.
- •1.2.7.Обчислення границь .
- •1.2.8. Границя при X → 0. (1-а надзвичайна границя).
- •1.2.9. Число е. (2-га надзвичайна границя ).
- •1.2.10. Неперервність функції в точці.
- •1.2.11. Властивості функції, неперервної на замкнутому інтервалі .
- •Змістовний модуль 2 Елементи математичної статистики
- •Тема 2.1. Елементи комбінаторики.
- •2.1.1.Основні поняття комбінаторики
- •Комбінації елементів, перестановки, розміщення.
- •Тема 2.2 . Елементи теорії ймовірностей
- •Ймовірність випадкової події
- •2.2.2.Теореми додавання та множення ймовірностей
- •Наслідки теореми додавання та множення ймовірностей
- •Формула повної ймовірності
- •Повторення випробувань
- •Тема 2.3 . Елементи математичної статистики.
- •2.3.1. Випадкові величини
- •2.3.2. Закон розподілу
- •2.3.3. Функція розподілу
- •2.3.4. Числові характеристики випадкової величини
- •Змістовний модуль 3 Застосування похідної та інтеграла
- •Тема 3.1. Похідна.
- •3.1.1. Означення похідної функції.
- •3.1.2. Геометричний зміст похідної
- •3.1.4. Правила диференціювання.
- •3.1.5. Додаток похідної в механіці.
- •3.1.6. Похідна складної функції.
- •3.1.7. Похідна зворотної функції.
- •3.1.8. Диференціал функції.
- •3.1.9. Геометрична інтерпретація диференціала функції.
- •3.1.10. Вживання диференціала в наближених обчисленнях.
- •3.1.11. Похідні і диференціали вищих порядків.
- •3.1.12. Правило Лопиталя.
- •Тема 3.2 Застосування похідної.
- •Поведінка функції в інтервалі.
- •3.2.2. Достатня ознака монотонності
- •3.2.3. Екстремуми функції.
- •3.2.4. Необхідна ознака екстремуму.
- •3.2.5. Достатня ознака екстремуму
- •3.2.6. Схема дослідження функцій на екстремуми.
- •3.2.7. Найбільше і найменше значення функції.
- •3.2.8 . Опуклість і угнутість графіка функції. Точки перегину.
- •3.2.9. Ознака точки перегину.
- •3.2.10. Асимптоти ліній.
- •3.2.11. Загальна схема дослідження функцій.
- •Тема 3.3 Невизначений інтеграл та його обчислення
- •3.3.1. Первісна функції та її властивості
- •Невизначений інтеграл
- •3.3.3. Властивості невизначеного інтегралу
- •3.3.4. Таблиця інтегралів
- •3.3.5. Основні методи інтегрування
- •3.3.6. Метод заміни змінної (метод підстановки)
- •3.3.7. Метод інтегрування за частинам
- •Тема 3.4. Визначений інтеграл. Застосування визначеного інтегралу
- •Поняття визначеного інтеграла
- •3.4.6. Обчислення площ плоских фігур, обмежених лініями:
- •3.4.7. Обчислення об'єму тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями:
- •Змістовний модуль 4 Диференційні рівняння
- •Тема 4.1 Диференційні рівняння
- •Задачі які приводять до диференційних рівнянь.
- •Основні поняття диференціальних рівнянь
- •Диференціальні рівняння першого порядку із змінними, що розділяються.
- •Тема 1.1 Функції, обчислення, властивості та графіки
- •Тема 1.2 Границі функції. Неперервність функції
- •Тема 2.1. Елементи комбінаторики.
- •Тема 2.2 . Елементи теорії ймовірностей
- •Тема 2.3 . Елементи математичної статистики.
- •Змістовний модуль 3 Застосування похідної та інтеграла
- •Тема 3.1. Похідна.
- •Тема 3.2 Застосування похідної.
- •Тема 3.3 Невизначений інтеграл та його обчислення
- •Тема 3.4. Визначений інтеграл. Застосування визначеного інтегралу
- •Змістовний модуль 4 Диференційні рівняння
- •Тема 4.1 Диференційні рівняння
- •Література
1.1.9. Основні елементарні функції.
В таблиці наведені найбільш важливі властивості та графіки основних елементарних функцій.
№ п/п |
Позначен ня функції |
D(y) |
E(y) |
Парність або непарність |
Монотонність |
Періодич- ність |
Графики функций |
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||||
1. Степена функція |
|||||||||||
1 |
|
(-∞;+∞) |
(-∞;+∞), якщо n –непарне; (0;+∞), якщо n – парне |
непарна, якщо n – непарне; парна, якщо n – парне |
зростає на (-∞;+∞),якщо n – непарне; спадає на
(- (0;+∞), якщо n – парне |
ні |
|
||||
2 |
|
(-∞;0) U U (0;+∞) |
(-∞;0) U U (0;+∞), якщо n –непарне; (0;+∞), якщо n – парне |
непарна, якщо n – непарне парна, якщо n – парне |
спадає на (-∞;+∞)якщо n – непарне; зростає на (-∞;0) та спадає на (0;+∞), якщоn – парне |
ні |
|
||||
3 |
n > 1 |
(-∞;+∞), если n – нечетно; (0;+∞), если n – четно |
(-∞;+∞), якщо n –непарне; (0;+∞), якщо n –парне |
непарна, якщо n – непарне; загального вигляду, якщо n – парне |
зростає на (-∞;+∞)якщо n – непарне; зростає на (0;+∞), якщоn – парне |
ні |
|
||||
2. Показникова функція |
|||||||||||
4 |
(а > 0, а ≠ 1) |
(-∞;+∞) |
(0;+∞) |
загального вигляду |
зростає на (-∞;+∞)якщо а > 1; спадає на (0;+∞), якщо 0 < а < 1
|
ні |
|
||||
3. Логаріфмична функція |
|||||||||||
5 |
|
(0;+∞) |
(-∞;+∞) |
загального вигляду |
зростає на (0;+∞) якщо а > 1; спадає на (0;+∞), якщо 0 < а < 1
|
ні |
|
||||
4. Тригонометричні функції |
|||||||||||
6 |
|
(-∞;+∞) |
(-1, 1) |
непарна |
зростає на (-π/2+2πn, π/2+2πn); спадає на (π/2+2πn, 3π/2+2πn),
|
період Т = 2π |
|
||||
7 |
|
(-∞;+∞) |
(-1, 1) |
парна |
зростає на (-π+2πn, 2πn); спадає на (2πn, π+2πn),
|
період Т = 2π |
|
||||
8 |
|
(-π/2+ +πn, π/2+πn);
|
(-∞;+∞) |
непарна |
зростає на (-π/2+πn, π/2+πn);
|
період Т = π |
|
||||
9 |
|
(πn, π+πn);
|
(-∞;+∞) |
непарна |
спадає на (πn, π+πn),
|
період Т = π |
|
||||

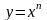
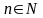
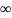 ;0),
зростає на
;0),
зростає на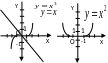

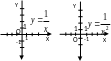
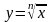

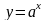
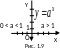
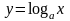 (а
> 0, а
≠ 1)
(а
> 0, а
≠ 1)