
- •Змістовний модуль 1 Функції та обчислення
- •Тема 1.1 Функції, обчислення, властивості та графіки
- •1.1.1Визначення та властивості функції.
- •1.1.2. Область визначення функції.
- •1.1.3. Способи завдання функції.
- •1.1.4. Парність та непарністьь.
- •4. Область визначення функції
- •1.1.5. Періодичність.
- •1.1.6. Монотонність .
- •1.1.7. Обмежені функції.
- •1.1.8. Перетворення графіків функцій.
- •1.1.9. Основні елементарні функції.
- •Тема 1.2. Границі функції. Неперервність функції
- •1.2.1. Границя функції f(X) якщо х стримиться до хо(х → хо).
- •1.2.2. Ліва та права границя функції .
- •1.2.3. Границя функції при X→ ∞.
- •1.2.4. Правила граничного переходу.
- •1.2.7.Обчислення границь .
- •1.2.8. Границя при X → 0. (1-а надзвичайна границя).
- •1.2.9. Число е. (2-га надзвичайна границя ).
- •1.2.10. Неперервність функції в точці.
- •1.2.11. Властивості функції, неперервної на замкнутому інтервалі .
- •Змістовний модуль 2 Елементи математичної статистики
- •Тема 2.1. Елементи комбінаторики.
- •2.1.1.Основні поняття комбінаторики
- •Комбінації елементів, перестановки, розміщення.
- •Тема 2.2 . Елементи теорії ймовірностей
- •Ймовірність випадкової події
- •2.2.2.Теореми додавання та множення ймовірностей
- •Наслідки теореми додавання та множення ймовірностей
- •Формула повної ймовірності
- •Повторення випробувань
- •Тема 2.3 . Елементи математичної статистики.
- •2.3.1. Випадкові величини
- •2.3.2. Закон розподілу
- •2.3.3. Функція розподілу
- •2.3.4. Числові характеристики випадкової величини
- •Змістовний модуль 3 Застосування похідної та інтеграла
- •Тема 3.1. Похідна.
- •3.1.1. Означення похідної функції.
- •3.1.2. Геометричний зміст похідної
- •3.1.4. Правила диференціювання.
- •3.1.5. Додаток похідної в механіці.
- •3.1.6. Похідна складної функції.
- •3.1.7. Похідна зворотної функції.
- •3.1.8. Диференціал функції.
- •3.1.9. Геометрична інтерпретація диференціала функції.
- •3.1.10. Вживання диференціала в наближених обчисленнях.
- •3.1.11. Похідні і диференціали вищих порядків.
- •3.1.12. Правило Лопиталя.
- •Тема 3.2 Застосування похідної.
- •Поведінка функції в інтервалі.
- •3.2.2. Достатня ознака монотонності
- •3.2.3. Екстремуми функції.
- •3.2.4. Необхідна ознака екстремуму.
- •3.2.5. Достатня ознака екстремуму
- •3.2.6. Схема дослідження функцій на екстремуми.
- •3.2.7. Найбільше і найменше значення функції.
- •3.2.8 . Опуклість і угнутість графіка функції. Точки перегину.
- •3.2.9. Ознака точки перегину.
- •3.2.10. Асимптоти ліній.
- •3.2.11. Загальна схема дослідження функцій.
- •Тема 3.3 Невизначений інтеграл та його обчислення
- •3.3.1. Первісна функції та її властивості
- •Невизначений інтеграл
- •3.3.3. Властивості невизначеного інтегралу
- •3.3.4. Таблиця інтегралів
- •3.3.5. Основні методи інтегрування
- •3.3.6. Метод заміни змінної (метод підстановки)
- •3.3.7. Метод інтегрування за частинам
- •Тема 3.4. Визначений інтеграл. Застосування визначеного інтегралу
- •Поняття визначеного інтеграла
- •3.4.6. Обчислення площ плоских фігур, обмежених лініями:
- •3.4.7. Обчислення об'єму тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями:
- •Змістовний модуль 4 Диференційні рівняння
- •Тема 4.1 Диференційні рівняння
- •Задачі які приводять до диференційних рівнянь.
- •Основні поняття диференціальних рівнянь
- •Диференціальні рівняння першого порядку із змінними, що розділяються.
- •Тема 1.1 Функції, обчислення, властивості та графіки
- •Тема 1.2 Границі функції. Неперервність функції
- •Тема 2.1. Елементи комбінаторики.
- •Тема 2.2 . Елементи теорії ймовірностей
- •Тема 2.3 . Елементи математичної статистики.
- •Змістовний модуль 3 Застосування похідної та інтеграла
- •Тема 3.1. Похідна.
- •Тема 3.2 Застосування похідної.
- •Тема 3.3 Невизначений інтеграл та його обчислення
- •Тема 3.4. Визначений інтеграл. Застосування визначеного інтегралу
- •Змістовний модуль 4 Диференційні рівняння
- •Тема 4.1 Диференційні рівняння
- •Література
3.1.11. Похідні і диференціали вищих порядків.
Хай
. Тоді похідна
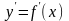 називається похідною першого порядку.
Вона у свою чергу є функцією х
і тому від неї можна узяти похідну, яка
називається похідною другого порядку
від вихідної функції
називається похідною першого порядку.
Вона у свою чергу є функцією х
і тому від неї можна узяти похідну, яка
називається похідною другого порядку
від вихідної функції
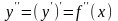
Аналогічно визначається похідна третього порядку
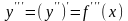
Подальші
похідні позначаються
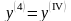 ,
,
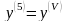 і далі.
і далі.
3.1.12. Правило Лопиталя.
Хай
функції
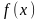 і
і
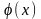 при
при
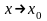 або
або
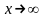 обидві прагнуть до нуля або нескінченності.
Якщо стосунки їх похідних має межу, то
відношення самих функцій має межу, рівну
межі відношення їх похідних.
обидві прагнуть до нуля або нескінченності.
Якщо стосунки їх похідних має межу, то
відношення самих функцій має межу, рівну
межі відношення їх похідних.
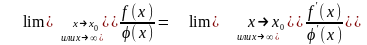
Приклад .
а)
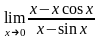 ; б)
; б)
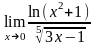 ;
;
а)
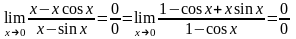 .
.
Тут
після вживання правила Лопіталя похідні
чисельника і знаменника у свою чергу
прагнуть до нуля. Застосовуючи правило
Лопіталя повторно, а у разі потреби і
далі,
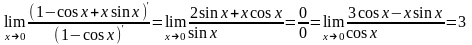 .
.
б)
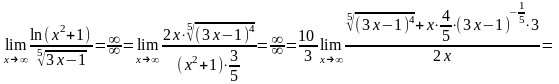
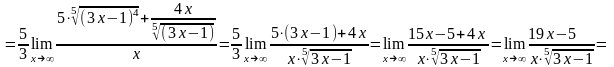
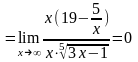 .
.
Тема 3.2 Застосування похідної.
Поведінка функції в інтервалі.
Одне з найважливіших призначень диференціального числення – застосування його до дослідження функцій, тобто до характеристики поведінки функції при зміні незалежній змінній. Це дослідження засноване на зв'язку, що існує між властивостями функції і її похідних (перш за все її першою похідною).
3.2.2. Достатня ознака монотонності
1. Якщо
похідна
 від функції
усюди
в інтервалі додатня, то функція в цьому
інтервалі зростає.
від функції
усюди
в інтервалі додатня, то функція в цьому
інтервалі зростає.
2. Якщо похідна від функції усюди в інтервалі від'ємна , то функція в цьому інтервалі убуває.
3. Якщо похідна від функції усюди в інтервалі дорівнює нулю, то функція в цьому інтервалі не змінюється (є константа).
Ця пропозиція формулює простий і зручну аналітичну ознаку монотонності функції в інтервалі.
Мал.1
Якщо рухлива точка М (x,y) при русі по графіку функції зліва направо, тобто при зростанні абсциси, піднімається, то дотична до графіка утворює з віссю ОХ гострий кут, тангенс якого додатний ; якщо ж точка М(x,y) опускається, то дотична до утворює з віссю ОХ тупий кут, тангенс якого від'ємний.
Слід
підкреслити, що похідна монотонної
функції в окремих крапках перетворюється
на нуль. Так, наприклад, функція
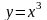 (мал. 2) зростає на всій осі ОХ,
але її похідна
(мал. 2) зростає на всій осі ОХ,
але її похідна
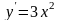 перетворюється
на нуль в точці х
= 0,
будучи позитивною у всіх останніх
точках.
перетворюється
на нуль в точці х
= 0,
будучи позитивною у всіх останніх
точках.
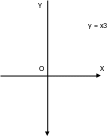
Мал. 2.
Геометричний сенс цього факту такий: дотична до графіка монотонної функції в окремих крапках може бути паралельна осі ОХ.
Таким чином, в інтервалі монотонності функції знак її похідної не може змінитися на зворотний.
Приклад
Знайти
інтервали монотонності функції
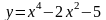 .
.
Знайдемо похідну
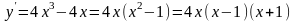
Визначимо знаки похідної за допомогою інтервалів.

Функція спадає на (-∞, -1) та (0,1) зростає на (-1,0) та (1,+∞)
3.2.3. Екстремуми функції.
Особливу роль в дослідженні функцій грають значення х, що відокремлюють інтервал зростання від інтервалу убування або інтервал убування від інтервалу зростання (мал. 3).

Мал.3.
У
цих точках функція
міняє характер своєї зміни; під час
переходу незалежної змінної через ці
крапки функція
з тієї, що зростає стає такою, що убуває
(графік І на мал.3) або навпаки, з тієї,
що убуває – що зростає (графік ІІ на
мал. 3). Якщо має місце перший випадок
(точка х΄
на мал. 3 відокремлює інтервал зростання
від інтервалу убування), то існує така
околиця точки х΄,
що значення
 є найбільшим значенням функції
в цій околиці; якщо має місце другий
випадок, (точка х˝
на мал. 3 відокремлює інтервал убування
від інтервалу зростання), то існує така
околиця точки х˝
, що значення
є найменшим значенням функції
в
цій околиці.
є найбільшим значенням функції
в цій околиці; якщо має місце другий
випадок, (точка х˝
на мал. 3 відокремлює інтервал убування
від інтервалу зростання), то існує така
околиця точки х˝
, що значення
є найменшим значенням функції
в
цій околиці.
Визначення. Точка хо називається точкою максимуму функції , якщо є найбільше значення функції в деякій околиці точки хо ;
аналогічно
Точка хо називається точкою мінімуму, якщо є найменше значення функції в деякій околиці точки хо .
Точки максимуму і мінімуму об'єднуються загальною назвою точки екстремуму. Функція на даному інтервалі може мати декілька екстремумів, причому який-небудь мінімум функції може виявитися більше якого-небудь максимуму (мал.4).
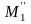
Мал.4
