73

Зміст

Змістовний модуль 1. Функції та обчислення

Тема 1.1 Функції, обчислення, властивості та графіки 2

Тема 1.2 Границі функції. Неперервність функції 8

Змістовний модуль 2. Елементи математичної статистики

Тема 2.1. Елементи комбінаторики. 21

Тема 2.2 . Елементи теорії ймовірностей. 22

Тема 2.3 . Елементи математичної статистики. 26

Змістовний модуль 3. Застосування похідної та інтеграла

Тема 3.1. Похідна функції. 28

Тема 3.2 Застосування похідної. 37

Тема 3.3 Невизначений інтеграл та його обчислення 49

Тема 3.4 Визначений інтеграл. Застосування визначеного інтегралу 53

Змістовний модуль 4. Диференційні рівняння

Тема 4.1 Диференційні рівняння 61

Завдання до самостійної роботи 64

Змістовний модуль 1 Функції та обчислення

Тема 1.1 Функції, обчислення, властивості та графіки

1.1.1Визначення та властивості функції.

Розглянемо дві множини значень дійсних чисел x та y. Нехай між ними є якась залежність. Поміж 2-х змінних одну приймають за незалежну (аргумент),який зазвичай позначають буквою х. Тоді друга зміна у буде залежати х. символічно залежність у та х позначається однією з букв f, φ, ψ, F, Ф та інш. І записується у вигляді y = f (x) або F (x, y) = 0.

Під символами f, φ, ψ, ... розуміється послідовність визначених математичних операцій с змінною х, які приводять до значення у.

Визначення. Закон (правіло), за яким кожному значенню незалежної змінної х відповідає тільки одне значення залежної змінної у, називається функцією.

1.1.2. Область визначення функції.

Визначення. Областю визначення функції називається множина значень незалежної змінної (аргументу), для яких функція зазначена, тобто має дійсне значення.

Область визначення функції позначають D (f).

При знаходженні області визначення функції, яка задана формулою y = f (x), треба сходити із наступних міркувань:

1. Якщо формула має радикали парної степені, тоді функція буде визначена тільки для тих значень х, для яких підкореневий вираз буде невід'ємним;

2. Якщо формула має дрібний вираз, тоді функція буде визначена тільки для тих значень х, для яких знаменник відмінний від 0;

3. Якщо формула має логарифмічну, показникові або тригонометричну функції, тоді область визначення визначається областю визначення цих функцій.

Приклади.

1. ;

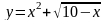Надана функція у складається з двох функцій и .

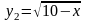Перша функція визначена на (– ∞ , + ∞).

Друга функція визначена при умовах 10 - х ≥ 0 або х ≤ 10, т.е. на проміжку (– ∞, 10), тоді D (f) = (– ∞, 10).

2. ;

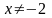D (f) = (– ∞, – 2) U (– 2, + ∞).

3. ;

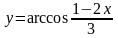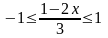
Розв'яжемо подвійну нерівність. Із лівої частини нерівності маємо:

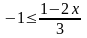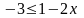, або , , .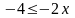

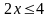Із правої частини нерівності маємо:

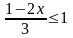
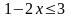
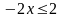
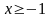
D (f) = [-1;2].

Визначення. Множина, яка складається із всіх чисел y = f(x), де х належить області визначення функції f, називають областю значень функції f та позначають E(f).

1.1.3. Способи завдання функції.

Функція вважається наданной, якщо для кожного аргументу можливо вказати значення функції. Існує три найбільш розповсюджених способи завдання функції:

а) таблично;

б) графічно;

в) аналітично.

а) Табличний спосіб загальновідомий ( таблиці логарифмів, тригонометричних функцій тощо). В цьому способі для наданих дискретних значень аргументу вказані числові значення функції;

б) графічний спосіб складається в зображені графіка функції - множини точок (х,у) площини, абсциси яких є аргументом, а ординати відповідні значення функції y = f(x);

в) аналітичний спосіб, якщо функція надана за допомогою формули y = f(x). Цей спосіб найбільш часто зустрічається на практиці. Так, функція _{надана аналітично функція може бути надана у вигляді аналітичного вираження, складающегося із двох або більш формул, для кожної із яких є її область визначення. Так. Наприклад надана функція :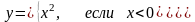} має два аналітичних вираза : х² (при х < 0) та х + 3 (при х ≥ 0). Функція, надана аналітично, може бути в явній та неявній формі.

Явна форма- функція надана у вигляді формули, яка вказує операції та послідовність їх виконання. Котрі потрібно виконати з незалежною змінною, щоб отримати значення залежної змінної. Наприклад, .

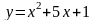Під неявним завданням функції розуміється надання функції у вигляді рівняння F(x, y) = 0. В цьому випадку залежну зміну не можна розв'язати відносно аргументу. Наприклад, .

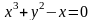Аналітично функція може бути задана в параметричній формі.

При параметричному завданні функції відповідні значення змінних х та у виражаються через третю змінну, яка зветься параметром.

; .

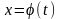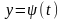Наприклад, функція х = sin t, y = cos t надана в параметричній формі .

Для того, щоб виразити залежність у від х в явній або неявній формі, треба в явной или неявной форме, треба виключити параметр t. Виключим параметр в цьому, для цього возведемо у квадрат обидві частини рівняння и додамо їх:

,

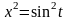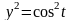
х² + у² = 1. Це рівняння описує коло с центром в початку координат, R = l.