Практическое занятие по теме: «Действия над матрицами»

Цель занятия: Научиться выполнять действия с матрицами: умножение матриц, нахождение линейных комбинаций матриц, транспонирование матриц.

Матрицей размера m×n называется прямоугольная матрица вида:

1. Суммой двух матриц А и В одинакового размера называется матрица А+В, получающаяся из А и В попарным сложением из элементов, стоящих на одинаковых местах.

2. Произведением матрицы А на число λ называется λА, получающаяся из А умножением числа λ на каждый её элемент.

3. Произведением (m×n)-матрицы А на (n×l)-матрицу В называется (m×l)-матрица А*В=С, каждый из элементов которой определяется по формуле: , то есть представляет собой сумму парных произведений элементов i-й строки первого сомножителя на соответствующие им по порядку следования элементы j-го столбца второго сомножителя (C_ij-элемент, состоящий на пересечении i-й строки и j-го столбца матрицы С).

Операция умножения матриц выполнима только тогда, когда число столбцов первой матрицы = числу строк второй матрицы.

1. Найти матрицу, противоположную матрице А = .

Решение. Для нахождения противоположной матрицы умножаем матрицу А на к = -1: - А = .

2. Найти линейную комбинацию 3А - 2В, если

А = , В = .

Решение. Сначала находим произведение А на к₁ = 3 и В на к₂ = -2:

3А = , - 2В = .

Теперь найдем сумму полученных матриц:

3А - 2В = = .

3. Найти произведение АВ, если А = , В = .

Решение. АВ = = .

4. Найти произведение АВ:

а) А = , В = Ответ: .

б) А = , В = Ответ: .

5. Вычислить С = А² + 2В, где А = , В = .

Ответ: .

6. Найти АВ - ВА, где А = , В =

Ответ: .

7. Найти АЕ, если А = , Е =

Ответ: .

8. Дана матрица . Найти обратную матрицу А^-1 методом алгебраических дополнений.

Найдем определитель матрицы

Найдем алгебраические дополнения каждого элемента матрицы

, ,

, ,

, ,

Запишем матрицу А^* , в которой элементы земенены их алгебраическими дополнениями и произведено транспонирование:

;

Разделим каждый элемент этой матрицы на определитель матрицы

Задания для самостоятельного решения Вариант 1

1. Вычислить произведение матриц А и В, если

А= В=

2. Найти обратную матрицу А^-1 для матрицы

А=

3. Решить матричное уравнение X*A=B, где

А= 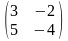В=

Вариант 2

1. Вычислить произведение матриц А и В, если

А= В=

2. Найти обратную матрицу А^-1 для матрицы

А=

3. Решить матричное уравнение и найти матрицу X.

x

Вариант 3

1. Вычислить произведение матриц А и В, если

А= В=

2. Найти обратную матрицу А^-1 для матрицы

А=

3. Решить матричное уравнение и найти матрицу X.

Вариант 4

1. Вычислить произведение матриц А и В, если

А= В=

2. Найти обратную матрицу А^-1 для матрицы

А=

3. Решить матричное уравнение и найти матрицу X.

Домашнее задание.

1. Вычислить линейные комбинации матриц:

а) 2А - В, если А = , В =

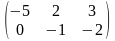
Ответ: .

б) 3А + 2В, если А = , В =

Ответ: .

2. Найти произведение АВ:

а) А = , В = Ответ: .

б) А = , В = Ответ: .

3. Найти , если А = , В =

Ответ: .

Вопросы для повторения.

1. Определение матрицы и ее обозначение.

2. Линейные операции над матрицами (сложение матриц и умножение матрицы на число).

3. Умножение квадратных матриц третьего порядка.

4. Правила умножения прямоугольных матриц.

5. Виды матриц.

6. Равные матрицы. Транспонированная матрица.

7. Умножение квадратных матриц второго порядка.

8. Свойства умножения матриц.