Сформулюємо практичне правило перевірки нулової гіпотези
Нехай
за незалежними вибірками об’ємів
та
,
зробленими із нормально розподілених
генеральних сукупностей, обчислені
виправлені вибіркові дисперсії
і
.
При
заданому рівні значущості
перевірку нульової гіпотези
про рівність дисперсій двох нормально
розподілених генеральних сукупностей
проводять за схемою :
Обчислюють спостережуване значення критерію як відношення більшої виправленої дисперсії до меншої :
.
2. А) Альтернативна гіпотеза .
З таблиці
критичних точок розподілу Фішера-Снедекора
(таблиця № 9 додатку 2) за рівнем значущості
і числами ступенів вільності
і
(
- об’єм вибірки, виправлена дисперсія
якої більша) знаходять критичну точку
розподілу
.
Якщо
- нульову гіпотезу приймають.
Якщо
- нульову гіпотезу відхиляють.
б)
Альтернативна гіпотеза
.
З таблиці
критичних точок розподілу Фішера-Снедекора
(таблиця № 9 додатку 2) за рівнем значущості
і числами ступенів вільності
і
(
- об’єм вибірки, виправлена дисперсія
якої більша) знаходять критичну точку
розподілу
.
Якщо - нульову гіпотезу приймають.
Якщо - нульову гіпотезу відхиляють.
Приклад 6.4
За
вибірками об’єми
яких
,
зробленими із двох нормально розподілених
генеральних сукупностей,обчислено
виправлені вибіркові дисперсії
і
.
При рівні значущості
перевірити нульову гіпотезу
про рівність дисперсій при альтернативній
гіпотезі
.
Порівнюємо дисперсії взявши відношення більшої до меншої :
.
2. Критична область двостороння, оскільки альтернативна гіпотеза .
Числа
і
ступенів вільності дорівнюють відповідно
:
(бо дисперсія
більша)
.
З таблиці
критичних точок розподілу Фішера-Снедекора
(таблиця № 9 додатку 2) за числами
,
знаходимо критичну точку розподілу
.
Оскільки - то нульову гіпотезу приймаємо.
Приклад 6.5
Для
порівняння точності двох станків-автоматів
взято дві проби-вибірки, об’єми
яких
і
обчислено виправлені вибіркові дисперсії
контрольованого розміру відібраних
виробів
і
.Чи
є підстави вважати, що перший станок
забезпечує кращу точність?
Оскільки
точність визначається дисперсією, то
за умовою нульовою гіпотезою буде
,
альтернативною -
.
Порівнюємо дисперсії взявши відношення більшої до меншої:
.
Критична
область одностороння (правостороння),
оскільки альтернативна гіпотеза
.
Числа ступенів вільності дорівнюють відповідно
,
(бо
дисперсія
).
З таблиці
критичних точок розподілу Фішера-Снедекора
(таблиця № 7 додатку 2) за рівнем значущості
і числами ступенів вільності
9
,
7
знаходимо критичну точку розподілу
.
Оскільки - то нульову гіпотезу приймаємо.
Отже, перший станок забезпечує менше розсіяння значень контрольованого розміру.
6.2.3 Порівняння дисперсій декількох нормально розподілених генеральних сукупностей.
а)Критерій Бартлетта (вибірки різних об’ємів)
Нехай
із генеральних сукупностей
розподілених нормально зроблено
незалежні вибірки різних об’ємів
,
за якими знайдено виправлені дисперсії
.
Для перевірки нульової гіпотези
про однорідність дисперсій використовують
критерій Бартлетта – випадкову величину
,
де
,
,
,
.
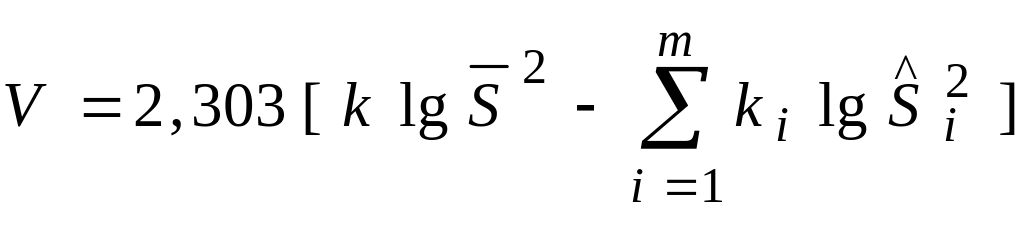Бартлетт
довів, що при справедливості нульової
гіпотези розподіл випадкової величини
наближається до розподілу
з (
)
ступенями вільності, якщо
(
).
Оскільки
,
то з умови
випливає, що об’єм
кожної із вибірок має бути не меншим
ніж 4.
Критична
область – правостороння. Критичну точку
знаходять з таблиці критичних точок
розподілу
(таблиця
№7 додатку 2) за рівнем значущості
і числом ступенів вільності
.
При
заданому рівні значущості
перевірку нульової гіпотези
про однорідність дисперсій проводять
за схемою :
1.
Одним із методів обчислюють виправлені
вибіркові дисперсії
.
2.
Обчислюють спостережуване значення
критерію
.
3.
З таблиці критичних точок розподілу
за рівнем значущості
і числом ступенів вільності
(
- число вибірок) знаходять критичну
точку
правосторонньої критичної області.
Якщо
- нульову гіпотезу приймають.
Якщо
- нульову гіпотезу відхиляють.
Зауваження 1
Оскільки
,
то обчисливши
порівнюють його з
.
Якщо
,
то обчислювати
не потрібно, якщо ж
,
то з
порівнюють
.
Зауваження 2
Оскільки критерій Бартлетта дуже чутливий до відхилень нормального розподілу, то до висновків за результатами цього критерію відносяться обережно.
Зауваження 3
При умові однорідності дисперсій за оцінку генеральної дисперсії беруть середнє арифметичне виправлених дисперсій
.
Всі обчислення для перевірки критерію Бартлетта зручно проводити за розрахунковою таблицею виду
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Номер вибірки |
Об’єм вибірки |
Число ступенів вільності |
Виправлені дисперсії |
|
|
|
|
|
|
|
|
|
|
|
|
В останній стрічці якої проводять сумування в третьому, п’ятому і сьомому стовпцях.