2.8 Электрическая цепь с индуктивным элементом

Индуктивная катушка элемент электрической цепи, характеризуемый индуктивностью. Индуктивность – коэффициент пропорциональности между током в катушке и потокосцеплением с витками катушки от этого тока . Индуктивность возрастает с увеличением числа витков и уменьшением магнитного сопротивления потоку вокруг витков катушки. Индуктивность определяет энергию магнитного поля, создаваемую этим током.

Рис. 2.12. Электрическая цепь с индуктивностью L

а – схема; б – изменение ЭДС самоиндукции, напряжения и тока; в – векторная диаграмма.

Пусть к зажимам цепи с индуктивностью (рис. 2.12) приложено напряжение источника питания . Для сокращения записи примем .

Под действием напряжения в цепи возникает синусоидальный ток . Этот ток создает синусоидальный магнитный поток с потокосцеплением катушки , где  — число витков катушки.

Согласно закону электромагнитной индукции, на зажимах катушки появится ЭДС самоиндукции

.

Знак минус согласно принципу электромагнитной инерции, сформулированному Ленцем, указывает на то, что ЭДС самоиндукции всегда имеет такое направление, при котором она препятствует изменению магнитного потока или тока в цепи.

Для катушки выбираем связь . Это соответствует тому, что при возрастании тока увеличивается энергия магнитного поля в катушке и мощность на ее зажимах положительна. Тем самым выбираем, что условно положительные направления стрелок падения напряжения на катушке совпадает с условно положительным направлением тока .

Условное положительное направление для ЭДС следует принимать таким же как для , так как при этом в согласии со связью всегда действительные направления и будут противоположны.

По второму закону Кирхгофа

,

, откуда

, интегрируя

, где

. В цепи с индуктивностью ток отстает по фазе от напряжения со сдвигом .

Величина имеет размерность сопротивления и называется индуктивным сопротивлением.

Для амплитуд и действующих значений

, .

В комплексной форме для действующих значений ток цепи

сокращая на ,

,

где  — индуктивная проводимость.

Умножение вектора напряжения на соответствует повороту вектора тока на угол в отрицательном направлении по часовой стрелке. Вектор тока отстает от вектора напряжения. Фазовый сдвиг между током и напряжением .

2.9 Электрическая цепь с емкостным элементом

Конденсатор элемент электрической цепи, характеризуемый емкостью. Емкость отношение заряда конденсатора к разности потенциалов между его обкладками. Емкость пропорциональна площади обкладок и проницаемости диэлектрика, обратно пропорциональна расстоянию между обкладками. Емкость определяет энергию электрического поля, создаваемого зарядом конденсатора.

Под действием приложенного к конденсатору напряжения происходит поляризация диэлектрика, то есть смещение заряженных частиц, входящих в состав молекул его вещества, в противоположных направлениях. Электрически нейтральные при отсутствии внешнего электрического поля молекулы диэлектрика превращаются в электрические диполи, то есть системы двух противоположных по знаку точечных зарядов. В процессе поляризации в диэлектрике происходит движение элементарных частиц в пределах молекулы, образующее ток поляризации, или ток смещения.

Пусть к зажимам цепи с емкостью (рис. 2.13) приложено напряжение .

Под действием напряжения в цепи возникает синусоидальный ток и на каждой пластине конденсатора скапливается заряд , где  — напряжение на конденсаторе.

Рис. 2. 13. Электрическая цепь с емкостью С

а – схема; б – изменение напряжения и тока; в – векторная диаграмма.

Условное положительные направления падения напряжения на конденсаторе совпадает с условно положительным направлением тока . Это соответствует тому, что при зарядке конденсатора энергия поступает в него и мощность на его зажимах положительна.

По второму закону Кирхгофа для данной цепи имеем . Тогда заряд на конденсаторе

.

По определению ток

, где

. В цепи с емкостью ток опережает по фазе напряжение со сдвигом .

Величина имеет размерность сопротивления и называется емкостным сопротивлением.

Для амплитуд и действующих значений

, .

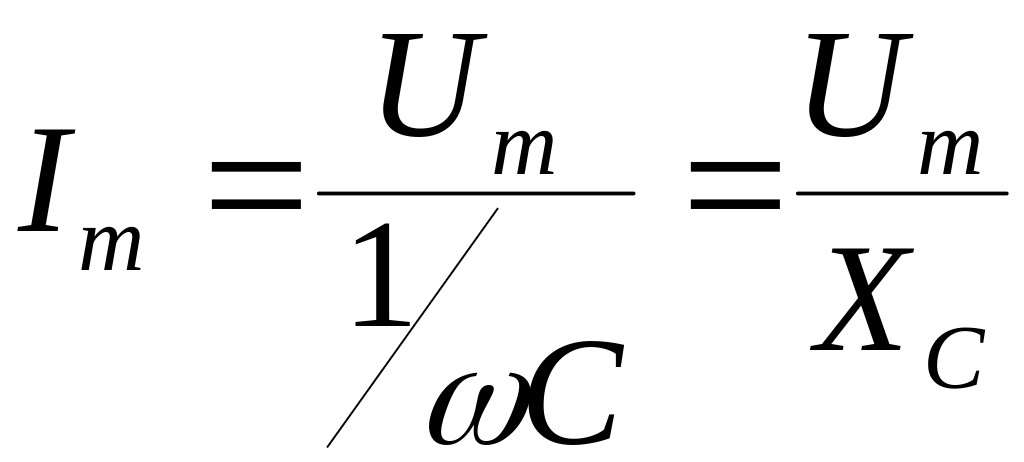В комплексной форме для действующих значений ток цепи

,

сокращая на ,

,

где - реактивная емкостная проводимость.

Умножение вектора напряжения на соответствует повороту вектора тока на угол в положительном направлении против часовой стрелки. Вектор тока опережает напряжение. Фазовый сдвиг между током и напряжением .