1.5 Комплексный метод расчета

Действие с векторами удобно представить действиями с комплексными числами.

Представим вращающийся вектор , соответствующий синусоидальной функции комплексной функцией . Комплексная функция может быть представлена

а) в тригонометрической форме:

б) в показательной форме:

где

- комплексная амплитуда,

 — мнимая единица,

- соотношение, вытекающее из формулы Эйлера;

— действительная часть комплексной функции (проекция вектора на ось вещественных чисел , Real axis);

 — мнимая часть комплексной функции (проекция вектора на ось мнимых чисел , Imaginary axis);

- модуль комплексной функции;

— главное значение аргумента комплексной функции, причем

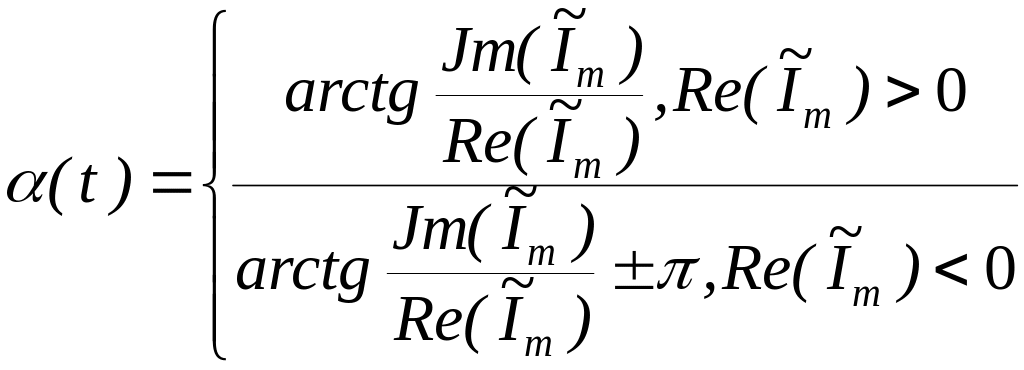
Фаза временной комплексной функции отсчитывается от положительного направления оси вещественных комплексной плоскости против часовой стрелки.

Умножение любого комплексного числа на (оператор поворота) приводит к изменению его аргумента на угол и повороту соответствующего вектора на тот же угол. Поскольку , то умножение комплексного числа на приводит к повороту вектора на угол  .

Так как , то .

Две комплексные функции, имеющие равные модули, но противоположные по знаку аргументы, называются сопряженными. Для сопряженных функций .

Рассмотрим синусоидальный ток

и комплексную функцию

Рис. 2.7. Изображение комплексной функции вращающемся вектором на комплексной плоскости

Данная комплексная функция представляет аналитическую запись вектора с модулем , вращающегося в комплексной плоскости с постоянной угловой скоростью , равной угловой частоте синусоидального тока, в направлении, противоположном движению часовой стрелки (рис. 2.7).

Справедливы соотношения

,

,

то есть синусоидальный ток равен проекции на ось мнимых величин вращающегося вектора, изображающего комплексную функцию.

Таким образом, синусоидальному току (оригиналу) может быть поставлена в соответствие комплексная функция (изображение) . Условная запись такого преобразования имеет вид

.

Аналогичные преобразования могут быть выполнены для синусоидальных напряжений и ЭДС

, .

Над комплексными функциями, изображающими синусоидальные ЭДС, напряжения и токи, можно производить все алгебраические действия.

В установившемся режиме интерес представляют фазовые сдвиги между векторами. Разделив комплексные функции на множитель , соответствующий временному вращению вектора, вычисления проводят относительно комплексных амплитуд: ; ; . При этом начальную фазу задающей физической величины (обычно напряжения) принимают равной нулю. В этом случае задающий вектор на комплексной плоскости будет совпадать с осью вещественных величин . При этом синусоидальный оригинал изображения в начальный момент времени равен нулю, а косинусоидальная функция равна единице. Комплексные действующие величины тока, ЭДС и напряжения

, ,

где - действующие значения.

Таким образом, при комплексном изображении синусоидальных величин в показательной форме в качестве модуля следует брать действующее значение синусоидальной величины, а в качестве аргумента — ее начальную фазу.

Производная и интеграл для синусоидального тока

,

Аналогично для напряжения и ЭДС.

Используя указанные преобразования, систему дифференциальных уравнений для действительных функций времени можно заменить системой алгебраических уравнений с комплексными токами, напряжениями и ЭДС.

Комплексный метод расчета электрических цепей синусоидального тока применим только при установившихся режимах.

Комплексный метод расчета электрических цепей полезно сопровождать построением векторных диаграмм на комплексной плоскости для момента времени .

Комплексные ток , напряжение , ЭДС и выражаемые через них комплексные сопротивление и комплексная проводимость  не являются физическими величинами и поэтому не имеют никакого физического смысла, а значит, и единиц измерения.