Решение нулевого варианта РГР по УрЧП

Задание 1

(а) Разложить функцию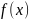 в ряд Фурье на указанном промежутке. Нарисовать график функции, определяющей сумму ряда.

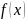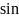(б) Разложить функцию в ряд Фурье по кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.

(в) Разложить функцию в ряд Фурье по кратных дуг на промежутке от 0 до правой границы указанного промежутка. Нарисовать график функции, определяющей сумму ряда.

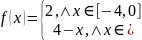
Решение:

(а) Построим график функции и ее периодического продолжения на всю ось (график выделен на рисунке жирной линией):

Имеем период . Тогда ряд Фурье имеет вид

График совпадает с графиком в точках непрерывности, а в точках разрыва :

Коэффициенты Фурье находим по формулам

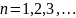
Получаем

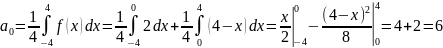
и, учитывая, что 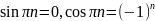, находим

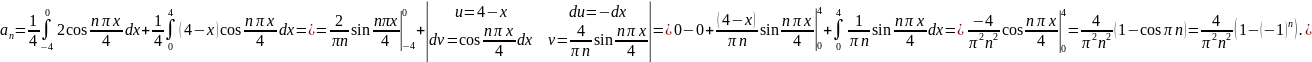
Итак,

Находим

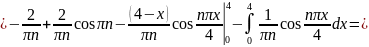
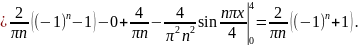
Итак, .

Подставляем найденные коэффициенты в ряд Фурье (*), окончательно имеем:

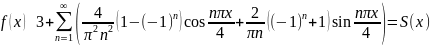
(б) Разложим функцию , по синусам кратных дуг в ряд Фурье. Продолжим нечетным образом на отрезок , а потом периодически продолжим на всю ось:

Имеем период . Тогда ряд Фурье по синусам имеет вид

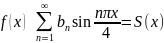
причем функция совпадает с продолженной функцией в точках непрерывности, а в точках разрыва имеем :

Находим :

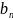Итак, .

Окончательно имеем

(в) Теперь разложим функцию , по косинусам кратных дуг в ряд Фурье. Продолжим эту функцию четным образом на отрезок , а потом периодически продолжим на всю ось, в качестве периода взяв :

Поскольку продолженная функция непрерывна на всей числовой прямой, то сумма ряда 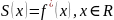, а сам ряд имеет вид:

Находим коэффициенты :

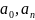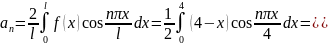
Итак,

Ряд Фурье имеет вид

Задание 2

Найти общее решение и решение, удовлетворяющее указанным начальным условиям для квазилинейного уравнения первого порядка

Решение:

Для решения квазилинейного уравнения в частных производных первого порядка относительно функции 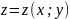запишем систему обыкновенных дифференциальных уравнений вида

Решаем эту систему сначала для одной пары, а потом для другой пары дифференциальных уравнений.

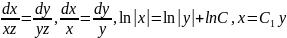
Рассмотрим другую пару

из полученного решения первой пары выражаем , а именно , и подставляем в это уравнение

Тогда общее решение исходного уравнения имеет вид 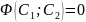, где - произвольная функция двух аргументов.

Имеем 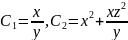и общее решение .

Поскольку функция входит в один из аргументов функции , то можно выразить этот аргумент через другой с помощью произвольной функции одной переменной :

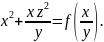
Это и есть общее решение.

Найдем вид функции из дополнительных условий 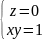. Тогда , то есть 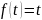. Имеем частное решение или

Проверка:

Функция задана неявно.

.

Тогда найдем

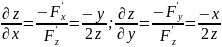
Подставим в исходное уравнение и получим тождество:

Задание 3

Методом характеристик привести уравнение к каноническому виду и найти решение задачи Коши.

;

Решение:

Исходное уравнение представляет собой линейное однородное уравнение в частных производных второго порядка

где 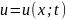- искомая функция, .

Определяем тип уравнения:

то есть это уравнение гиперболического типа. Составляем характеристическое уравнение и решаем его.

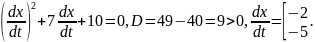
Получаем две характеристики

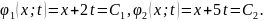
Переходим к новым переменным . Тогда

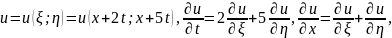
Подставим в исходное уравнение:

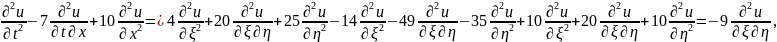
а значит, по условию

Получаем каноническое уравнение для гиперболического типа .

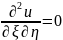Решаем это уравнение.

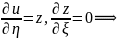
где - произвольные функции. Заменяем и получаем общее решение .

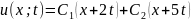Теперь решаем задачу Коши, то есть находим функции из начальных условий .

Решаем систему относительно .

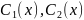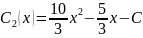
Подставим в общее решение:

Получаем частное решение задачи Коши

Проверка:

Найденная функция удовлетворяет условию задачи Коши:

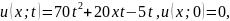
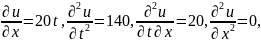
т.е.