2. Кінематичне дослідження механізмів

Знаходження положень ланок, траєкторій, що описуються певними точками ланок, переміщень, швидкостей і прискорень, кутових швид­костей і прискорень ланок є задачами кінематичного дослідження ме­ханізмів. Визначають кінематичні параметри графічним, графоаналітичним, аналітичним і експериментальним методами.

2.1. Побудова планів механізмів

Для визначення положень ланок механізму треба мати кінематич­ну схему механізму, закон руху ведучої ланки й розміри ланок. Ланки механізму, швидкості та прискорення певних його точок зображатимемо у вигляді ліній певної довжини. Для цього скористуємося масштабним коефіцієнтом, який е відношенням зображуваної величини до відповід­ного відрізка на кресленні. Масштабний коефіцієнт, який скорочено називають масштабом, позначимо літерою μ з індексом того параметра, який зображено графічно. Наприклад, масштабний коефіцієнт довжини ланок

м/мм.

Побудова плану положень механізму виконується графічно методом засічок.

Нехай треба визначити положення ланок та траєкторії точок механізму, кінематична схема якого задана. Розміри ланок та закон руху ведучої ланки ОА задано.l_OA=0,3 м; l_AB=0,8; l_BC=0,65м; l_BD=0,23м; l_OE=y=1,1 мl_EC=х=0,09 м; ₁=0°; ₂=90; ₁=20 c^-1

Центри ваги ланок знаходяться на серединах ланок.

Так як ланка ОА обертається з постійною кутовою швидкістю навколо точки О, то траєкторію точки А є коло радіусом ОА.

Із точки О проводимо коло радіусом 30 мм, тоді масштабний коефіцієнт довжини _l ⁼ l_ОА/ОА=0,3 м /30 мм =0,01 м/мм Поділимо коло на 12 однакових частин. Позначимо положення кривошипа ОА в напрямі обертання його А₁, А₂, А₃ і т.д.

По заданим розмірам ланок в масштабі _l знаходимо положення нерухомих точок механізму О і С. З точки С проводимо дугу радіусом СВ.

СВ= l_CВ/ μ_l= 0,65 м/0,01 м/мм=65 мм.

Послідовно, із кожної точки А (А₁, А₂, A₃ і т.д.) дугою АВ робимо на цій дузі засічки. Так знаходимо 12 положень точки В.

АВ=l_ав/μ_l =0,8 м/0,01 м/мм =80 мм.

Послідовно з'єднуємо точки А і В, В і С. Одержуємо 12 положень механізму. З точки С проводимо дугу СД і одержуємо траєкторію руху точки Д.

СД = (l_CB+l_BD)/μ_l= (0,65 м+0,23 м)/0,01 м/мм = 88 мм.

Центри ваги ланок знаходяться на серединах ланок.

2.2. Будування кінематичних діаграм.

Перевага методу кінематичних діаграм– наочність і простота. Розглянемо цей метод на прикладі кривошипно-повзунного механізму, 12 планів якого побудовано раніше. Використавши здобуті дані, спочатку побудуємо графік переміщення S_Д повзуна як функцію часу t, а потім гра­фічним диференціюванням дістанемо графіки швидкості V_Д і приско­рення a_Д повзуна .

Для побудови діаграми переміщення – час на осі абсцис відкладемо відрізок X мм, що в масштабі буде часом одного повного оберту кривошипа:

,

де n - частота обертання кривошипа, хв.^-1;

- масштаб часу, с/мм.

Поділимо-відрізок X на 12 рівних частин і в точках 1,2...12 відкладемо вздовж осі ординат відрізки УІ,У2_Г..УІ2, які в масштабі зображають переміщення повзуна Д від крайнього лівого положен­ня Д₀ за І/12 оберту кривошипа /відповідно 1В₁=У1, 2В₂=У2, 3В₃=У3.

Сполучивши точки 0,Д_І,Д₂,Д₃..Д_ІІ плавною кривою, дістанемо діаграму пройдених шляхів S_Д= S_Д(t).

Кутова швидкість ведучої ланки ОА

ω₁=20 с^-1=20 рад/с

Величина швидкості точки А ведучої ланки механізму:

V_а= ω₁·l_OA=20·0,3=6 м/с

Вектор швидкості точки А спрямований перпендикулярно ланці ОА в напрямку її обертання.

Із точки Рv – полюса плану швидкостей – проводимо вектор мм, що зображає швидкість точки А у масштабі:

.

Вектор проводимо перпендикулярно ланці ОА напрямку обертання.

Для групи 2-3 складаємо систему векторних рівнянь.

.

Швидкість точки А відомо по значенню і напряму. Відносна швидкість відома за напрямом – вона перпендикулярна ланці АВ, але невідома за величиною. Швидкість точки С=0, , тобто вона знаходиться у полюсі Р_v. Відносна швидкість перпендикулярна ланці ВС, але невідома за величиною.

З кінця вектора на плані швидкостей проводимо лінію, перпендикулярну ланці АВ, а з полюса р_v – лінію, перпендикулярну ланці ВС. Точка перетину цих ліній позначимо b. Вектор зображає на плані швидкостей абсолютну швидкість точки В, ії модуль дорівнює:

V_В=р_vbμ_v=200,2=4 [м/с].

Відносна швидкість зображена на плані швидкостей відрізком і ії модуль дорівнює:

V_ва=bа μ_v=29 0,2=5,8 [м/с].

Для знаходження швидкості точки Д скористаємося теоремою подібності фігур, які утворюють вектори відносних швидкостей і фігури на плані механізму.

Фігура відносних швидкостей на плані швидкостей подібна фігурі на плані механізму, але повернена відносно останньої на 90° у напрямі кутової швидкості фігури механізму.

[мм].

Відклавши на продовженні відрізка ( ) відрізок bd=7 мм одержимо точку d. Модуль абсолютної швидкості точки Д:

V_ДВ=р_Vd_V=70,2=1,4 [м/с].

Швидкості центрів ваги знаходимо теж за теоремою подібності:

[м/с];

[м/с];

[м/с].

Кутова швидкість ланки ОА відома =20 с^-1 має напрям проти руху годинникової стрілки. Кутова швидкість ланки АВ

с^-1.

Ця швидкість має напрям проти руху годинникової стрілки. Для знаходження цього перенесемо уявно відрізок ( ), що зображує у точку В механізму. Він показує в якому напрямку обертається точка В і всі інші точки ланки АВ навколо точки А.

Кутова швидкість ланки СД

с^-1

і має напрям по годинникової стрілці. Для визначення цього перенесемо уявно відрізок ( ), що зображає у точку В механізму. Він показує, в якому напрямку обертається точка В і всі інші точки ланки ВС навколо точки С.

Побудова плану прискорень здійснюється в тій ж послідовності, що і план швидкостей.

а_А=а_О+а_АО; а_О=0, то а_А=а_АО

.

Так як ланка АО рухається рівномірно (V_A=const), то а^_AO⁼0. Тоді

[м/с²].

В ектор має напрям уздовж ланки ОА від точки А до точки О, тобто до центру обертання.

З точки р_а – полюса плану прискорень – проводимо відрізок довільної довжини ( мм), що зображає вектор прискорення а_А в масштабі

.

Відрізок проводимо паралельно ОА у напрямі від точки А до точки О.

Для групи 2-3 складаємо векторну систему рівнянь

.

Прискорення точки А відоме за модулем, значенню і напрямом. Прискорення точки С дорівнює 0, тобто точка С знаходиться у полюсі. Прискорення аⁿ_ва паралельне ВА і спрямоване від точки В до точки А. Значення цього прискорення

[м/с²].

Прискорення а^_АВ перпендикулярне ВА. Модуль цього прискорення поки що невідомий.

Прискорення аⁿ_BC паралельне ВС і спрямоване від точки В до точки С. Модуль цього прискорення

[м/с²].

Прискорення а^_АВ перпендикулярно ВС, модуль цього прискорення поки що невідоме. З кінця вектора проводимо пряму, паралельну ВА, у напрямі від точки В до точки А. На ній відкладаємо вектор , що зображує прискорення аⁿ_BA Величина цього вектора

[мм].

З точки п проводимо пряму, перпендикулярну, що зображує напрям а^_AB.

З полюса р_а, тобто з точки С, проводимо пряму, паралельну ВС у напрямі від точки В до точки С. На ній відкладаємо вектор , що зображує прискорення аⁿ_BС .Величина цього вектора

[мм].

З точки т проводимо пряму, перпендикулярну ВС, яка зображує напрям а^_ВС. Точка перетину цього перпендикуляру з перпендикуляром, проведеним з точки п, позначимо точкою b. З’єднаємо точку b з полюсом І точкою а.

Абсолютне прискорення точки В

[м/с²].

Відносне прискорення

[м/с²].

Для знаходження прискорень точки Д та центрів ваги, скористаємося теоремою подібності фігур, утворених векторами відносних прискорень і фігур на плані механізму:

Фігура відносних прискорень на плані прискорень подібна фігурі на плані механізму, але повернена відносно неї на 180° - у напрямі кутового прискорення фігури. Кут  визначається з рівності.

.

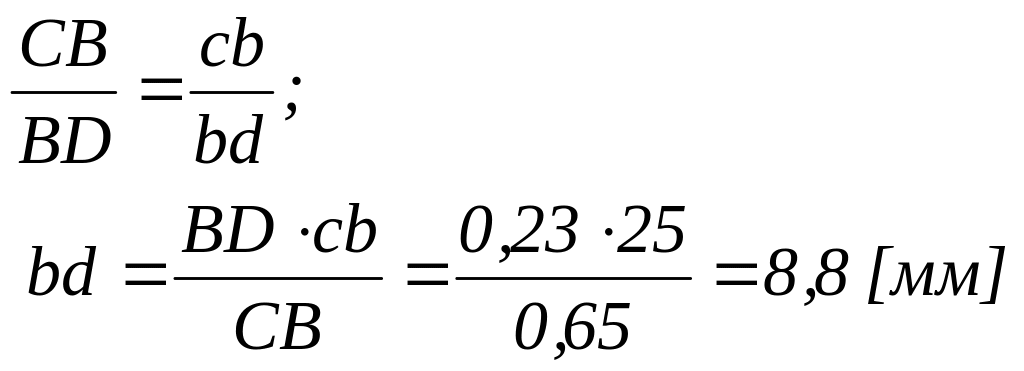
Відклавши на продовженні вектора відрізок bd=8,8 мм, одержуємо точку d.

Модуль абсолютного прискорення точки Д

[м/с²].

Модулі тангенціальних прискорень та прискорень центрів ваги:

[м/с²];

[м/с²];

[м/с²];

[м/с²];

[м/с²].

Кутове прискорення ланки ОА дорівнює 0.

Кутове прискорення ланки АВ

[с^-2].

Це прискорення спрямоване проти руху годинникової стрілки. Щоб визначити його напрям, переносимо уявно вектор а^_BA (відрізок (mb)) в точку В механізму і розглядаємо рух цієї точки відносно точки А по напряму прискорення а^_BA.

[с^-2]

і має напрям проти годинникової стрілки.