5.8. Сложение взаимно перпендикулярных колебаний

Изучим результирующее колебание при сложении двух колебаний с одинаковыми циклическими частотами ω, происходящих во взаимно перпендикулярных направлениях вдоль осей Х и Y.

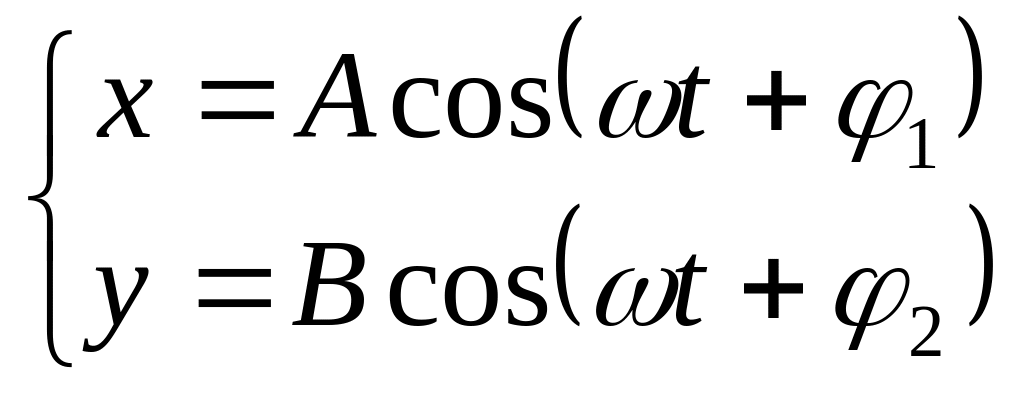(5.46)

Для определения уравнения траектории результирующего движения, необходимо из (5.46) исключить время t . Для этого раскроем косинус суммы углов, затем умножим первое уравнение на сos φ₂ , второе на cos φ₁ и вычтем из первого уравнения второе

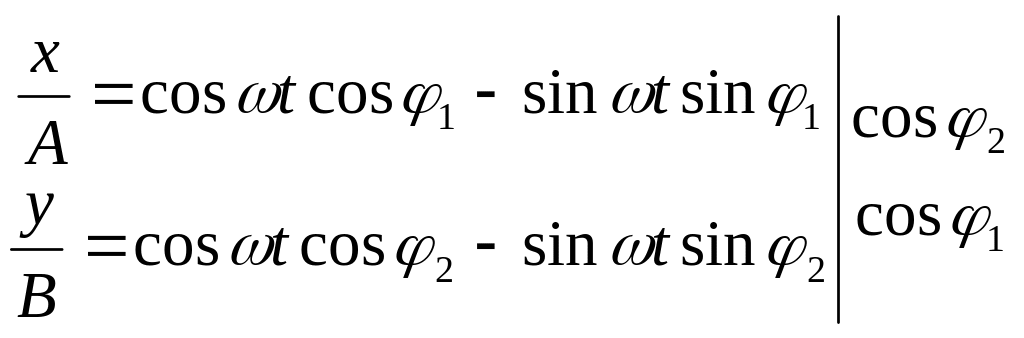(5.47)

После этих преобразований получим

(5.48)

Аналогичные действия произведем, умножив уравнения (5.47) на sin φ₂ и sin φ₁

(5.49)

Возводя в квадрат (5.48) и (5.49) и складывая, получим уравнение эллипса

(5.50)

Рассмотрим некоторые частные случаи

1) Пусть разность фаз φ₂ – φ₁ = 0

Уравнение (5.50) примет вид

или

Отсюда – уравнение прямой (рис.5.13).

Результирующее колебание точки происходит по прямой, составляющей с осью ОХ угол, тангенс которого равен . Точка совершает гармонические колебания с циклической частотой ω и амплитудой .

2) При разности фаз φ₂ – φ₁ = π. уравнение (5.50) примет вид . Тогда – уравнение прямой (рис.5.14). Результирующее колебание также гармоническое с частотой ω происходит по прямой около центра О, наклоненной к ОХ под углом большим на π/2.

Рис.5.13 Рис.5.14

Иными словами, при значениях φ₂ – φ₁ = kπ. (k = 0, 1, 2, …) в уравнение (5.50) , и мы получаем уравнение прямой .

3) При уравнение траектории будет представлять собой эллипс

При равенстве амплитуд А + В = R эллипс превращается в окружность

При сложении взаимно перпендикулярных колебаний разных, но кратных между собой частот (например, и т.д.), получаются различные траектории материальной точки, называемые фигурами Лиссажу (рис.5.15).

Рис.5.15

Вид фигур зависит от соотношения частот ω₁/ω₂ и разности начальных фаз (φ₂ – φ₁) слагаемых колебаний.

Исследования частот и разности фаз складываемых колебаний с помощью фигур Лиссажу широко используется на практике, особенно в измерительной технике.

К началу

К следующей лекции к содержанию

К титулу