Математический маятник

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, которая колеблется под действием силы тяжести.

Момент инерции материальной точки относительно оси вращения проходящей через точку подвеса равен

Математический маятник является частным случаем физического маятника, поэтому, период колебаний математического маятника можно вычислить по формуле (5.24), учитывая, что приведенная длина физического маятника и длина математического маятника равны (L = l)

.

2. Затухание колебания

Движение в реальных системах всегда сопровождается трением и в результате потери энергии колебания затухают. Свободные колебания всегда являются затухающими. Затухающие колебания можно продемонстрировать с помощью установки изображенной на рис.5.6. Если привести в колебание воронку с песком, то при ее движении всыпающийся песок оставляет след затухающих колебаний.

Рис.5.6

При малых скоростях колебания сила трения пропорциональна скорости

(5.25)

где r – коэффициент сопротивления.

На колеблющуюся систему массой m действует сумма сил ( ), которая вызывает ускорение этой системы, т.е.

или

(5.26)

Зная, что и, обозначив (α – коэффициент затухания), получим дифференциальное уравнение затухающих колебаний

(5.27)

Решением этого уравнения при условии ω₀ > α является выражение

(5.28)

Здесь – частота затухающих колебаний, а постоянные А₀ и φ зависят от начальных условий.

На рис.5.7. представлен график функции (5.28). На графике пунктиром показаны кривые затухания амплитуд. Уменьшение амплитуд происходит по закону

(5.29)

где α – коэффициент затухания, характеризующий скорость затухания колебаний.

Рис.5.7

Найдем время τ, в течение которого амплитуда уменьшается в е раз. Если в формулу (5.29) подставить , получим

 = 1 или .

Следовательно, коэффициент затухания обратно пропорционален времени, за которое амплитуда уменьшается в е раз.

Мерой затухания является величина называемая логарифмическим декрементом затухания δ. Логарифмический декремент затухания есть логарифм отношения двух последовательных амплитуд колебаний отличающихся на период.

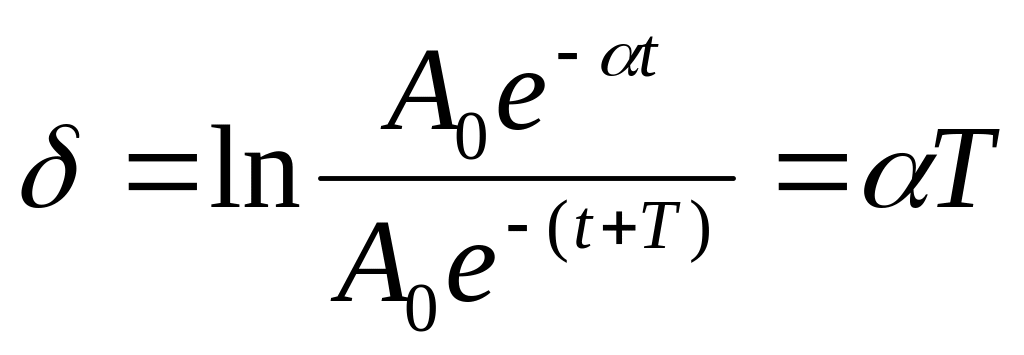(5.30)

При малых значениях δ пользуются понятием добротности .

Период затухающих колебаний равен

При система совершает периодические затухающие колебания, как показано на рис.5.8.

Когда , то Τ  ∞. Это значит, что движение перестает быть периодическим (см. рис.5.8). В зависимости от начальных условий система возвращается в положение равновесия по одной из двух указанных кривых.

2. Вынужденные колебания. Резонанс

Колебания реальной системы всегда происходят с трением и с течением времени они затухают. Чтобы колебания были незатухающими, необходимо компенсировать потери энергии воздействием на систему внешней силой.

Рис.5.8

Наиболее простой случай, когда внешняя сила F изменяется по гармоническому закону

(5.31)

где F₀ – амплитудное значение силы,

ω – циклическая частота действия вынуждающей силы.

Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными.

К силам, действующим при свободных колебаниях (5.26), прибавляется вынуждающая сила

или

(5.32)

где , – коэффициент затухания;

– собственная циклическая частота колебаний системы.

Это неоднородное дифференциальное уравнение незатухающих колебаний, решение которого равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Установившиеся вынужденные колебания происходят по гармоническому закону с частотой, равной частоте внешней силы ω. В этом случае решением уравнения (5.32) будет

(5.33)

где, А – амплитуда, φ – сдвиг фаз между смещением и вынуждающей силой.

А и φ зависят от соотношений между ω и ω₀. Чтобы установить эти зависимости воспользуемся уравнением (5.33) и подставим в уравнение (5.32) значение х, , .

После соответствующих преобразований получим:

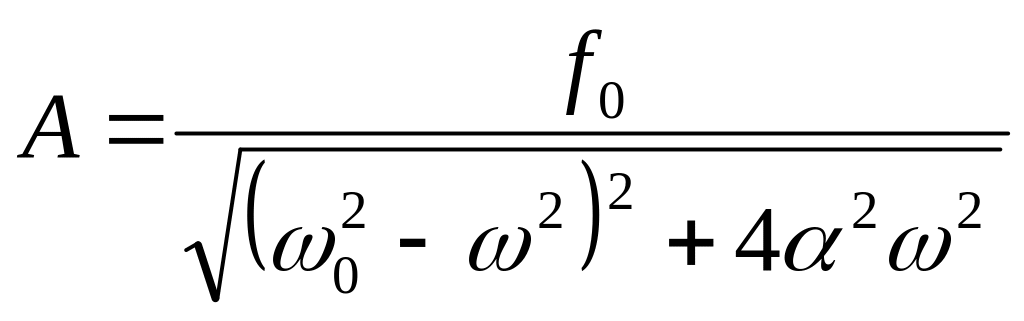(5.34)

и

(5.35)

Из выражения (5.34) видно, что амплитуда А зависит от частоты вынуждающей силы ω и при она максимальна. Резкое возрастания амплитуды вынужденных колебаний, когда циклические частоты вынуждающей силы и свободных колебаний близки друг к другу называется резонансом, а соответствующая частота – резонансной частотой. Резонансные кривые изображены на рис.5.9.

Из уравнения (5.34) видно, что при ω = 0

при ω ≈ ω₀ (при резонансе)

Рис.5.9

Из формулы (5.35) следует, что при ω = 0 φ = 0 фазы силы и колебания совпадают, а при резонансе (ω ≈ ω₀, φ = π/2) сила опережает колебания на π/2. При увеличении ω сдвиг фаз увеличивается и при ω >> ω₀, φ → π. Это значит, что фаза колебаний почти противоположна фазе вынуждающей силе.

В подтверждение сказанному можно продемонстрировать явление резонанса и сдвиг фаз на установке (рис.5.10). Если тяжелый правый маятник вывести из равновесия, то крайний левый, одинаковый по длине маятник, придет в резонанс и будет максимально отклоняться. При этом их колебания по фазе будут отличаться на π/2.

Рис.5.10

Явление резонанса может быть вредным и полезным. Явление резонанса учитывается в строительстве, используется в акустике, радиотехнике и т.д.