- •Лінійна алгебра Матриці та дії над ними
- •Розв’язання систем лінійних алгебраїчних рівнянь
- •Матричний метод розв’язання систем лінійних алгебраїчних рівнянь
- •Векторна алгебра Вектори. Лінійні операції над векторами
- •Скалярний добуток
- •Векторний добуток
- •Мішаний добуток
- •Аналітична геометрія на площині Прямокутна та полярна система координат. Побудова лінії за її рівнянням
- •Пряма лінія на площині
- •Розташування двох прямих на площині
- •Криві другого порядку
- •Аналітична геометрія у просторі Рівняння площини
- •Взаємне розташування двох площин у просторі
- •Пряма у просторі
- •Взаємне розташування двох прямих у просторі
- •Взаємне розміщення прямої та площини
- •Завдання Завдання 1.
- •Завдання 2.
- •Завдання 4.
Векторна алгебра Вектори. Лінійні операції над векторами
Визначення
Вектором називається величина, яка характеризується як числовим значенням, так і напрямом у просторі.
Числове значення вектора зветься довжиною або модулем вектора.
Звичайно
вектор позначають однією
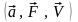 або двома латинськими літерами зі
стрілкою
або двома латинськими літерами зі
стрілкою
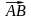 ,
або жирними літерами.
,
або жирними літерами.

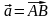 ,
точка
– початок вектора, точка
– його кінець.
,
точка
– початок вектора, точка
– його кінець.
Модулем або довжиною
вектора
називається число
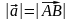 ,
яке дорівнює довжині відрізку
,
яке дорівнює довжині відрізку
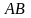 .
В фізиці часто модулі векторів позначають
відповідними літерами без стрілки:
.
В фізиці часто модулі векторів позначають
відповідними літерами без стрілки:
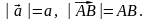
Визначення
Одиничним
вектором
або ортом
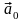 даного вектора
даного вектора
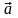 називається вектор, довжина якого
дорівнює одиниці довжини (при даному
масштабі), а напрям збігається з напрямом
,
тобто
називається вектор, довжина якого
дорівнює одиниці довжини (при даному
масштабі), а напрям збігається з напрямом
,
тобто
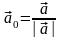 або
або
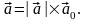
Орти
осей декартових координат позначаються
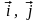 та
та
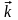 .
.
Визначення
Проекцією
вектора
на вісь
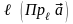 називається довжина відрізка, який
з’єднує проекції на цю вісь початку й
кінця даного вектора, взята зі знаком
“+”, якщо кут між вектором і віссю
гострий, і знаком “–”, якщо цей кут
тупий.
називається довжина відрізка, який
з’єднує проекції на цю вісь початку й
кінця даного вектора, взята зі знаком
“+”, якщо кут між вектором і віссю
гострий, і знаком “–”, якщо цей кут
тупий.
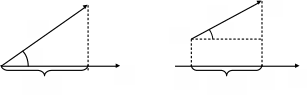 Із
вище наведеного рисунку ясно, що
Із
вище наведеного рисунку ясно, що
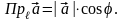
Будемо
у подальшому позначати проекції вектора
на координатні осі
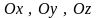 відповідно
відповідно
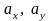 та
та
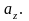 Вектор можна задати цими проекціями,
які називаються координатами вектора,
Вектор можна задати цими проекціями,
які називаються координатами вектора,
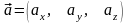 ,
,
або розкладанням за координатним базисом
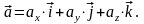
Визначення
Вектори
і
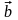 називаються колінеарними
називаються колінеарними
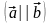 ,
якщо вони лежать на паралельних прямих
або на прямих, які збігаються.
,
якщо вони лежать на паралельних прямих
або на прямих, які збігаються.
Умова
колінеарності двох векторів
та
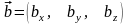 рівносильна умові їх пропорційності
рівносильна умові їх пропорційності
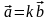 ,
тобто або
,
тобто або
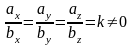 ,
або обидві відповідні координати цих
векторів одночасно дорівнюють нулю.
,
або обидві відповідні координати цих
векторів одночасно дорівнюють нулю.
Приклад
Обчислити
координати вектора
,
якщо відомі координати точок його
початку та кінця:
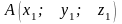 та
та
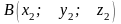 .
.
Розв’язання
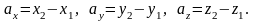
Тому
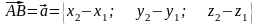 .
.
Відповідь:
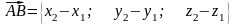 .
.
При додаванні, відніманні та множенні вектора на число відповідно додаються, віднімаються та множаться на це число одноіменні координати.
Приклад
Обчислити
суму та різницю двох векторів
 та
та
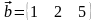 .
.
Розв’язання
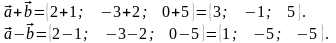
Відповідь:
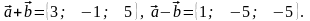
Приклад
Обчислити
добутки вектора
на числа
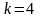 та
та
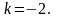
Розв’язання
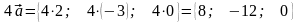 ,
,
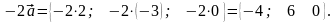
Відповідь:
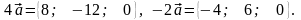
Розрізняють два види добутків двох векторів: скалярний та векторний.
Скалярний добуток
Визначення
Скалярним добутком двох векторів та називається число, яке дорівнює добутку модулів співмножників на косинус кута між ними:
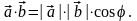
Використовуючи визначення проекції вектора, скалярний добуток можна записати так:
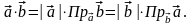
За допомогою скалярного добутку можна обчислити:
а) косинус кута між двома векторами
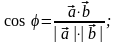
б) довжину вектора
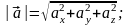
в) проекцію одного вектора на напрям іншого
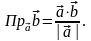
Якщо
вектори
та
взаємно перпендикулярні
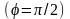 ,
їх скалярний добуток дорівнює нулю.
Використовуючи це, можна довести, що
скалярний добуток
,
їх скалярний добуток дорівнює нулю.
Використовуючи це, можна довести, що
скалярний добуток
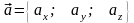 та
та
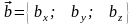 дорівнює
дорівнює
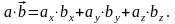
Звідси
маємо ознаку перпендикулярності векторів
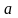 і
,
заданих координатами
і
,
заданих координатами
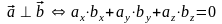 .
.
Приклад
Обчислити
внутрішній кут при вершині
трикутника
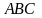 ,
якщо відомі його вершини: (3;
2; -3), (5;
1; -1), та С(1;
-2; 1).
,
якщо відомі його вершини: (3;
2; -3), (5;
1; -1), та С(1;
-2; 1).
Розв’язання
Внутрішній кут
при вершині А утворюється двома векторами
та
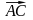 .
Обчислимо їх координати:
.
Обчислимо їх координати:
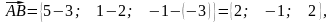
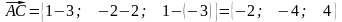 .
.
Їх
модулі:
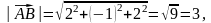
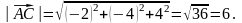
Скалярний добуток
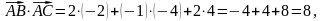
тоді
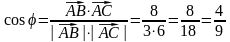 ,
,
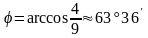 .
.
Відповідь:
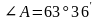 .
.
Визначення
Напрямними
косинусами вектора
називають косинуси кутів між вектором
і координатними осями, тобто
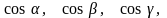 де
де
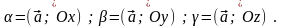
Якщо
,
тоді
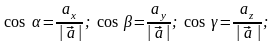
![]() ,
причому,
,
причому,
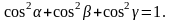
, причому,
Приклад
Обчислити
напрямні косинуси вектора
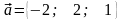 .
.
Розв’язання
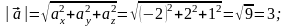
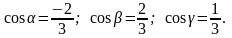
Перевіримо що
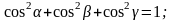
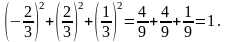
Відповідь: