УКРАЇНСЬКА ДЕРЖАВНА АКАДЕМІЯ ЗАЛІЗНИЧНОГО ТРАНСПОРТУ

Кафедра вищої математики

ЛІНІЙНА АЛГЕБРА ТА АНАЛІТИЧНА ГЕОМЕТРІЯ

МЕТОДИЧНІ ВКАЗІВКИ І ЗАВДАННЯ

для студентів 1 курсу загальнотехнічних спеціальностей заочної форми навчання

Харків 2000

Методичні вказівки розглянуті та рекомендовані до друку на засіданні кафедри вищої математики 31 серпня 2000 року, протокол № 1.

Методичні вказівки підготовлені з метою допомогти студентам в їх самостійній роботі при вивченні тем:

• “Лінійна та векторна алгебри”,

• “Аналітична геометрія на площині та в просторі”,

а також при виконанні контрольної роботи №1 студентами заочної форми навчання та розрахункових робіт для студентів денної форми навчання.

Склали: ст. викл. Н.І. Волохова, доц. Р.М. Давидов,

ст. викл. Л.І. Макаренко, доц. Н.С. Юрчак

Рецензент:  доц. В.А. Таратушка

Зміс

ЛІНІЙНА АЛГЕБРА 4

Матриці та дії над ними 4

Розв’язання систем лінійних алгебраїчних рівнянь 11

Матричний метод розв’язання систем лінійних алгебраїчних рівнянь 15

ВЕКТОРНА АЛГЕБРА 17

Вектори. Лінійні операції над векторами 17

Скалярний добуток 19

Векторний добуток 22

Мішаний добуток 23

АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ 26

Прямокутна та полярна система координат. Побудова лінії за її рівнянням 26

Пряма лінія на площині 27

Розташування двох прямих на площині 29

Криві другого порядку 34

АНАЛІТИЧНА ГЕОМЕТРІЯ У ПРОСТОРІ 38

Рівняння площини 38

Взаємне розташування двох площин у просторі 39

Пряма у просторі 40

Взаємне розташування двох прямих у просторі 41

Взаємне розміщення прямої та площини 41

ЗАВДАННЯ 44

Завдання 1. 44

Завдання 2. 45

Завдання 4. 46

ЛІНІЙНА АЛГЕБРА 15

Матриці та дії над ними 15

Розв’язання систем лінійних алгебраїчних рівнянь 15

Матричний метод розв’язання систем лінійних алгебраїчних рівнянь 15

ВЕКТОРНА АЛГЕБРА 16

Вектори. Лінійні операції над векторами 16

Скалярний добуток 18

Векторний добуток 21

Мішаний добуток 22

АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ 24

Прямокутна та полярна система координат. Побудова лінії за її рівнянням 24

Пряма лінія на площині 25

Розташування двох прямих на площині 27

Криві другого порядку 32

АНАЛІТИЧНА ГЕОМЕТРІЯ У ПРОСТОРІ 36

Рівняння площини 36

Взаємне розташування двох площин у просторі 37

Пряма у просторі 38

Взаємне розташування двох прямих у просторі 38

Взаємне розміщення прямої та площини 39

ЗАВДАННЯ 41

Завдання 1. 41

Завдання 2. 42

Завдання 3. 43

Завдання 4. 44

Завдання 5. 45

СПИСОК ЛІТЕРАТУРИ 46

Лінійна алгебра Матриці та дії над ними

Визначення

Матрицею розміру 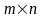називається упорядкована множина з елементів 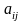, розміщених у вигляді прямокутної таблиці з 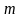рядків і 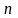стовпців.

.

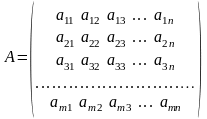Зауважимо, що на відміну від визначника матриця – це лише упорядкована таблиця елементів, а не результат виконання певних операцій; робити будь-які перестановки в ній не можна.

Приклади матриць: , , , .

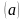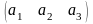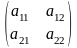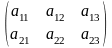Визначення

Матриця, всі елементи якої є нулі, називається нульовою матрицею відповідного розміру.

,   , , …

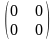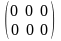Якщо 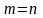, то матриця А – квадратна.

Визначення

Квадратна матриця, всі елементи головної діагоналі якої є одиниці, а решта – нулі, називається одиничною (відповідного розміру).

= , = .

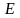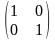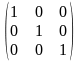1. Матриці однакового розміру можна додавати і віднімати за правилом:

=

= .

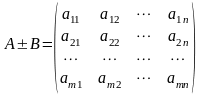
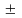
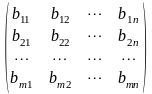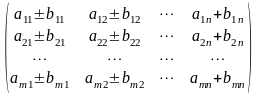2. Матриці довільного розміру можна умножити на число за правилом:

.

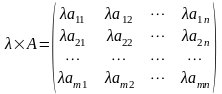3. Матрицю 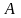розміру 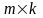можна умножити на матрицю 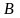розміру 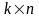якщо їх розміри узгоджені: кількість стовпців дорівнює кількості рядків . При цьому добутком 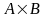є така матриця С розміру , елементи якої с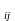 є сумами попарних добутків елементів 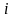-го рядка матриці на 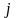-й стовпець матриці , тобто для всіх ,

.

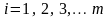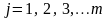
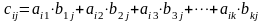4. Операція транспонування полягає в тому, що стовпці матриці замінюються рядками:

–

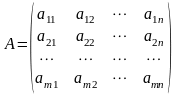
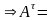
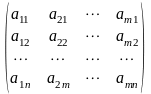транспонована матриця.

Приклад

Знайти 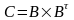, , 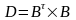якщо .

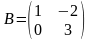Розв’язання

.

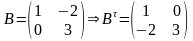Обчислимо:

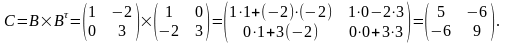
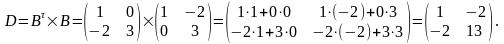
Отже: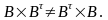

Для добутку матриць не має місця комутативний закон.

5. Кожній квадратній матриці ставиться у відповідність певне число, яке називається визначником матриці. Позначається визначник матриці А – det A і може записуватись у вигляді таблиці з елементів матриці, але у прямих рамках. Обчислюється визначник за наступними правилами:

Для матриці другого порядку .

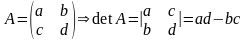Наприклад, .

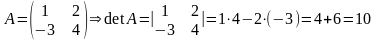Для матриці третього порядку .

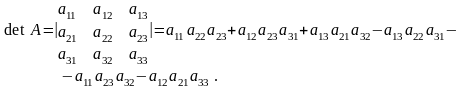Ц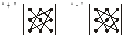 я формула ілюструється схемою, яка демонструє, які доданки при обчисленні визначника беруть зі знаком “+”, а які зі знаком “” і зветься “правилом трикутників”.

Наприклад,

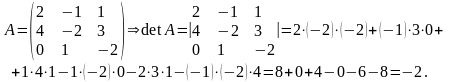
Визначники більш високого порядку обчислюються за допомогою так званого розкладання по елементах деякого рядка, або стовпчика.

Визначення

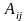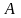Алгебраїчним доповненням елемента квадратної матриці n-го порядку називається число, яке дорівнює добутку визначника (n-1)-го порядку, отриманого із цієї матриці викресленням i-го рядка, та j-го стовпчика, на .

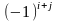Визначник квадратної матриці n-го порядку дорівнює сумі попарних добутків елементів будь якого рядка (або стовпчика) матриці та їх алгебраїчних доповнень.

.

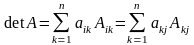Це правило відноситься рівною мірою і до визначників третього порядку. Найчастіше визначники обчислюють розкладанням по першому рядку, наприклад,

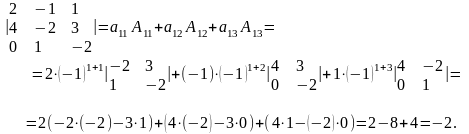
Визначення

Квадратна матриця називається невиродженою (неособливою), якщо її визначник .

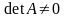Визначення

Матриця називається оберненою до невиродженої матриці , якщо

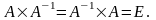
Обернену матрицю можна обчислити за формулою: ,

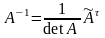де 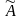– матриця, яка складається із алгебраїчних доповнень елементів матриці

,

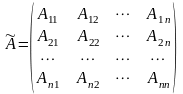– алгебраїчні доповнення елементів матриці .

Матриця називається приєднаною до матриці . Таким чином, маємо таку формулу для

.

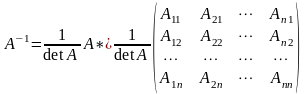Приклад

Знайти обернену матрицю до матриці

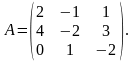
Розв’язання

Обернену матрицю мають тільки квадратні невироджені матриці. Визначник цієї матриці обчислювався в двох попередніх прикладах і 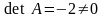. Отже матриця неособлива і має обернену

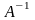
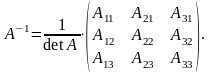
Знайдемо всі її алгебраїчні доповнення.

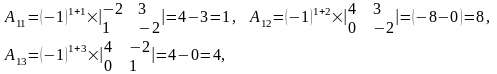
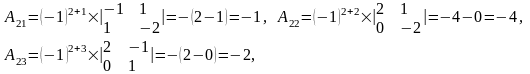
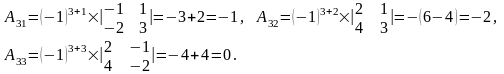
Отже

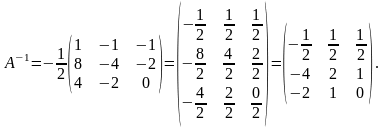
Тепер потрібно перевірити, що побудована матриця дійсно є оберненою до матриці , тобто перевірити, щ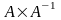о або 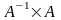дорівнює одиничній матриці.

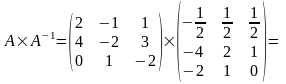
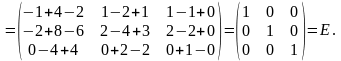
Відповідь: