
- •I.Сызықты дифференциалдық теңдеулер жүйесі
- •II. Біртекті сызықты жүйелерді матрицалық әдіспен интегралдау
- •I.Сызықты дифференциалдық теңдеулер жүйесі
- •Біртекті сызықты теңдеулер жүйесі
- •1.1.1 Біртекті жүйесінің шешімдерінің негізігі қасиеттері
- •1.1.2 Остроградский – Лиувилль– Якоби формуласы
- •1.1.3 Жалпы шешімін құру
- •1.2 Біртекті емес сызықты теңдеулер жүйесі
- •1.1.1 Біртекті емес жүйенің ортақ шешімінің құрылымы
- •1.2.2 Тұрақты ерік түрлендіру әдісі ( Лагранж әдісі)
- •II. Біртекті сызықты жүйелерді матрицалық әдіспен интегралдау
- •Матрица теориясынан кейбір мәліметтер
- •2.2 Матрицаларды дифференциалдау және интегралдау.
- •2.3 Біртекті сызықтық жүйенің матрицалық түрде жазылуы мен шешімі
- •Лаппо – Данилевский жағдайы
- •2.5 Тұрақты коэфициенттері бар біртекті сызықтық жүйені интегралдау
- •2.6 Сызықтық жүйелерді матрицалық-векторлық тәсілмен интегралдау
- •Біртекті матрицалық-векторлық теңдеуді шешудің негізгі қасиеттері
- •1Мысал.
1.1.1 Біртекті жүйесінің шешімдерінің негізігі қасиеттері
Біздің нақты тапсырмамыз (1.5) жүйені шешу жолдарын қарастыру. Бірақ бұл тапсырманы шешу үшін, n-ші ретті біртекті сызықтық теңдеу сияқты, кейде бірінші кейбір комплекстік шешімдерін табу ыңғайлылырақ. (1.5) Біртекті жүйенің комплекстік шешімі туралы ұғым енгізейік.
Комплекстік функцияның қосындысын нақты ауыспалыдан қарастырайық
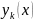 =
=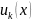 +
+
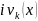 (1.9)
(1.9)
Мұндағы
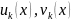 (k
)
нақты
ауыспалыдан нақты функция болып табылады.
(k
)
нақты
ауыспалыдан нақты функция болып табылады.
(1.9)
функцияның жиынтығын (a,b) аралығында
біртекті жүйенің (1.5) комплекстік шешімі
деп атаймыз, егер бұл функциялар a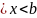 тепе-теңдігі үшін барлық жүйелердің
теңдіктерін қарастырса, яғни
тепе-теңдігі үшін барлық жүйелердің
теңдіктерін қарастырса, яғни
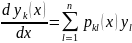 (k
)
(k
)
немесе
 +
I
+
I
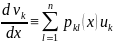 +
I
+
I
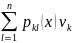 (1.10)
(1.10)
(k ).
).
Екі комплекс сандар өрісі бір-бірінің арасында өзара тең, тек сәйкесінше нақты және жорамал бөліктері тең болса. Олай болса, (1.10) тепе-теңдікте нақты және жорамал бөліктерін теңестіріп көреміз, егер (1.5) жүйе (1.9) комплекстік шешімге ие болса, онда оның екі нақты шешімі болады
(Ʀ ) ,
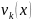 (Ʀ
)
,
(Ʀ
)
,
яғни функцияның нақты және жорамал бөліктері (1.5) біртекті сызықтық жүйенің (1.9)комплекстік шешімін құрушы, осы жүйеге екі нақты шешім құрады.
Біртекті сызықтық жүйенің шешімі (1.5) келесі қасиеттерге ие болады, n-ші ретті біртекті сызықтық теңдеуді ұқсастық қасиеттерімен шешу.
Егер
 (k
)
(1.11)
(k
)
(1.11)
(2) біртекті сызықтық жүйенің шешімі бар, онда
 (k
)
,
(1.12)
(k
)
,
(1.12)
Мұндағы C – тұрақты сан, ол да осы жүйенің шешімі болады, біртекті сызықтық жүйелердің шешімін құрушы, тұрақты біреуіне барлық функцияларды көбейтіп,біз тағыда шешімін аламыз.
Шынымен, (1.12) функцияны (1.5) жүйеге қойып,
(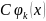 )ʼ
)ʼ

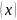 C
C
 (
(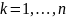 )
(1.13)
)
(1.13)
аламыз.
С-ға қысқартып, біз тепе-теңдік аламыз, (1.11) функция (1.5) жүйенің шешімі болғандықтан. Сондықтан (1.13) теңдік тепе-тең орындалады, дәлелдеу керегі де осы еді.
(1.5) жүйенің шешімі m болсын
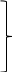
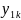 (
k
)
,
(
k
)
,
 (
k
)
,
(
k
)
,
. . . . . . . . . . (1.14)
 (
k
)
.
(
k
)
.
Мұндағы бірінші индекс шешімнің номерін білдіреді, ал екіншісі – функцияның номері.
Дәлелдейік, шешімнің (1.14) сызықтық тәсілі кез-келген тұрақты коэфициенттерімен
 ,
,
 ,
… ,
,
… ,
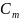 ,
яғни
функцияның жиыны
,
яғни
функцияның жиыны
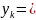
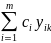 (
k
)
(1.15)
(
k
)
(1.15)
бұл да (1.5) жүйенің шешімі болады.
Шыныменде, (1.15)-і (1.5)-ге қойып, мынаны аламыз
(
) ʼ

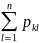 (
(
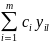 ) ( k
)
(1.16)
) ( k
)
(1.16)
немесе
ʼ
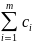
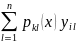 ) (
k
).
(1.17)
) (
k
).
(1.17)
Тепе-теңдік орынға ие болғандықтан
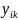 ʼ
ʼ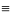
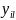 ( k
( k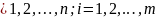 ),
(1.18)
),
(1.18)
(2)
жүйеге
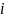 -нің
шешімін қойған, нәтижесі (14) теңдік болып
табылады, сәйкесінше, (13) теңдік те
тепе-тең орындалады, біздің дәлелдеу
керегіміз де осы еді.
-нің
шешімін қойған, нәтижесі (14) теңдік болып
табылады, сәйкесінше, (13) теңдік те
тепе-тең орындалады, біздің дәлелдеу
керегіміз де осы еді.
Енді бізге (2) біртекті жүйедегі n-нің жеке шешімі белгілі екенін болжайық. Басты сұрақ қойайық: қандай жағдайда сызықтық әрекет осылардың шешімдерінің негізсіз тұрақты коэфициенттерімен , , … , біртекті жүйенің жалпы шешімін береді.
Қойылған сұраққа жауап беру үшін, сызықты тәуелсіз жүйенің функциясы ұғымын енгіземіз.
