Контрольные вопросы

1. Что такое структурная схема САУ?

2. Каким образом можно составить структурную схему САУ?

3. Поясните типовые способы преобразования структурных схем САУ.

4. Что такое сигнальный граф?

5. Какие основные команды MatLab могут быть использованы для структурных преобразований САУ?

Лабораторная работа № 3 исследование устойчивости и качества линейной системы автоматического управления

Цель лабораторной работы - закрепление теоретических знаний по вопросам устойчивости и качества управления линейных систем автоматического управления (САУ) и практическое применение методов определения устойчивости и оценки качества линейных САУ.

Продолжительность лабораторной работы – 4 часа.

Работа предполагает решение следующих задач:

– расчет параметров линейной САУ в статическом режиме

– определение устойчивости линейной САУ

– поиск оптимальных параметров регулятора и моделирование переходных процессов в линейных САУ

1. Порядок выполнения работы

1. Выберите параметры элементов САУ (табл. 3.1) в соответствии с вариантом индивидуального задания.

Таблица 3.1

№№	g			№№	g			№№	g
1	0,5	0,2	0,19	6	3	0,3	0,14	11	5,5	0,4	0,15
2	1	0,4	0,28	7	3,5	0,5	0,23	12	6	0,6	0,24
3	1,5	0,6	0,37	8	4	0,7	0,32	13	6,5	0,8	0,33
4	2	0,8	0,46	9	4,5	0,9	0,41	14	7	0,1	0,42
5	2,5	0,1	0,55	10	5	0,2	0,9	15	7,5	0,3	0,51

2. Для САУ с П-регулятором рассчитать и построить график зависимости = f ( ) .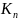

3. Моделированием получить экспериментальную зависимость = f ( ) для САУ с П-регулятором. Сопоставить результаты расчета с результатами моделирования.

4. Рассчитать область возможных (граничных) значений коэффициента передачи регулятора 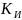(рис.3.1), при которых выполняется условие устойчивости САУ. Расчет выполнить отдельно для САУ с интегрирующим (И) регулятором и САУ с пропорционально-интегрирующим (ПИ) регулятором с учетом параметров звеньев в соответствии с индивидуальным заданием.

5. Смоделировать САУ с И и ПИ-регуляторами. Пронаблюдать величину статической ошибки, сделать выводы.

6. Проверить на модели выполнение условий устойчивости для САУ с И и ПИ-регуляторами. Сделать вывод об устойчивости САУ.

7. Смоделировать САУ с большей величиной коэффициента передачи регулятора, чем его граничное значение, определенное в п.4 программы. Пронаблюдать поведение неустойчивой САУ.

8. Для САУ с И и ПИ-регуляторами определить экспериментальные зависимости интегральной оценки от коэффициента передачи регулятора J₀=f( ) и построить их графики.

9. По графикам 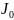(п.8 программы) определить оптимальные значения

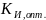
10. Для САУ с И и ПИ-регуляторами исследовать переходные процессы при различных значениях . Для каждого переходного процесса определить типовые показатели качества: величину перерегулирования, время переходного процесса и колебательность.