2. Порядок выполнения работы

1. С помощью команд пакета MatLab построить реакцию каждого типового звена (см. таблицу) на ступенчатое и импульсное входное воздействие. Определить влияние коэффициентов, входящих в описание каждого звена на параметры переходного процесса.

2. Рассчитать и построить переходные функции и частотные характеристики для одного из звеньев своего варианта, представленных в табл. 1.

3. Составить модели в MatLab/Simulink всех звеньев своего варианта.

4. Выполнить моделирование, получить переходные функции и частотные характеристики.

5. Сравнить результаты по п. 2 с результатами по п. 3; сделать выводы об адекватности проведенных исследований.

3. Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Передаточные функции и схемы моделирования исследуемых звеньев.

2. Экспериментально полученные характеристики при вариации параметров каждого звена.

3. Расчет и графики переходных, амплитудно-фазовых частотных, логарифмических амплитудных частотных и фазовых частотных характеристик, полученных в результате аналитического решения.

4. Модели в MatLab/Simulink и графики переходных, амплитудно фазовых частотных, логарифмических амплитудных частотных и фазовых частотных характеристик, полученных в результате имитационного моделирования.

5. Выводы о проделанной работе.

Методический пример по использованию пакета

MatLab/ Simulink

В пакете MatLab имеется два основных варианта для исследования передаточных функций и моделирования САУ:

– использование команд пакета расширения Control System Toolbox;

– использование пакета Simulink.

Control System Toolbox предназначен для работы с LTI-моделями (Linear Time Invariant Models – линейные модели с постоянными параметрами) систем управления.

Команда, создающая LTI-систему c одним входом и одним выходом в виде передаточной функции, имеет следующий синтаксис:

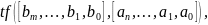
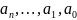где и - значения коэффициентов полиномов В и А в (3).

Например, если требуется описать ПФ вида:

и узнать значения ее нулей и полюсов, то нужно ввести в окне команд MatLab (рис .1.1) команды, по результатам которых выдаются сообщения о ее выполнении.

1. Главное окно системы matlab

>> w=tf([1 1],[2 8 5])

Transfer function:

s + 1

---------------

2 s^2 + 8 s + 5

>> zero(w)

ans =

-1

>> pole(w)

ans =

-3.2247

-0.7753

Исследовать реакцию LTI-модели на типовые входные воздействия можно с помощью команд step и impulse. По результатам выполнения команд выводятся графики рис. 1.2 и рис. 1.3

>> step(w)

2. Результат выполнения команды step (переходная характеристика)

>> impulse(w)

3. Результат выполнения команды impulse (импульсная характеристика)

Можно получить на одном графике реакцию сразу нескольких динамических звеньев, если использовать команды вида:

>> step(w,w1,w2)

>> impulse(w, w1,w2)

Время моделирования при этом выбирается автоматически. При необходимости время можно явно указать в команде

>> step(w, w1, w2, t),

где t – время моделирования в секундах.

Например, при вводе следующих команд

>> w=tf([1],[2 0.3 1]);

>> w1=tf([1],[2 0.5 1]);

>> w2=tf([1],[2 0.1 1]);

>> step(w,w1,w2,50)

получим рис 1.4.